Polaritet?
Hur byter spänningen polaritet när en ledare rör sig i en cirkel? Uppkommer detta när exempelvis en slinga är parallel med magnetfältet och sedan vänder riktning?
Kan du förklara närmare vad du menar med "en ledare som rör sig i en cirkel". Kan du rita en figur?
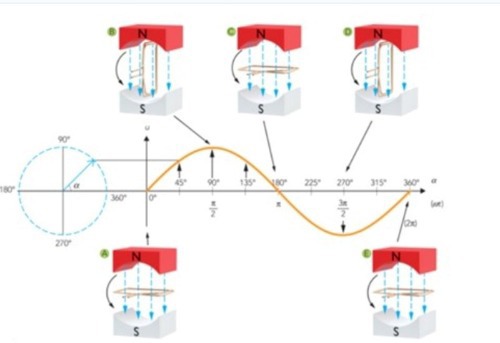
Lånad bild.
Ungefär så. En ledare, slinga eller vad det nu kan vara som snurrar runt ett magnetfält!
Bra! Det är mindre risk för missförstånd om vi pratar kring samma bild, det spelar såklart ingen roll vem som gjort den.
Vad är det för storhet på y-axeln? (bildens upplösning gör att jag inte kan se det)
På y-axeln är det lilla u (växelspänning) och på x-axeln
Enligt Faradays induktionslag gäller att den inducerade spänningen i ledarslingan är
där är det vinkelräta flödet genom ytan som slingan innesluter (varför det är just på det viset det fungerar är verkligen svårt att förstå, men detta är en matematisk modell som först beskrevs av Faraday. Vi får helt enkelt acceptera det just nu.)
Figuren antar att magnetfältet från permanentmagneten är konstant, och eftersom , så blir Det ger att den inducerade spänningen kan skrivas som
I figuren är det alltså när byter tecken, som gör att byter tecken (dvs byter polaritet).
Den mot magnetfältet vinkelräta inneslutna arean är maximal när slingan befinner sig i horisontalplanet i figuren vilket betyder att just i det ögonblicket byter tecken.
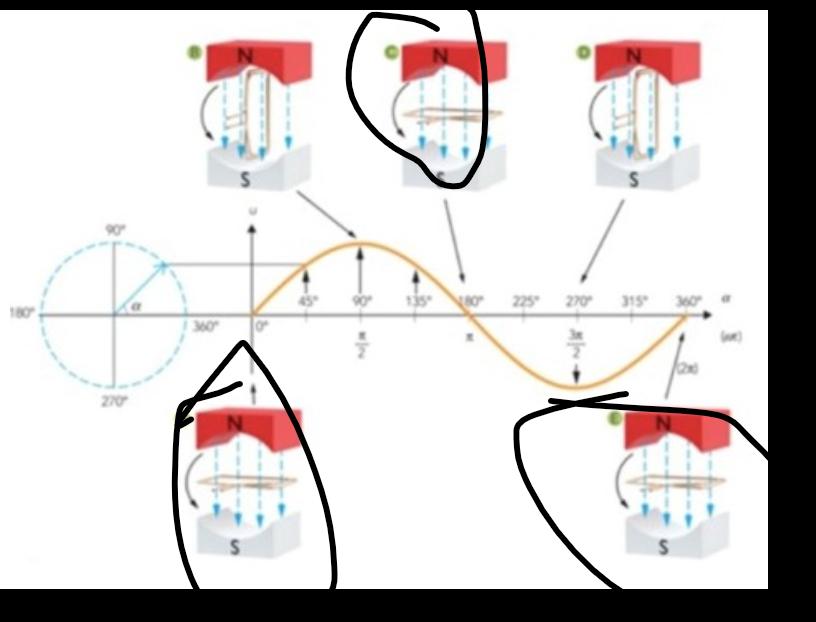
JohanF skrev:Enligt Faradays induktionslag gäller att den inducerade spänningen i ledarslingan är
(text)
Tack så mycket för ditt utförliga svar! Har lite funderingar nedan:
och eftersom ,
**** så blir Det ger att den inducerade spänningen kan skrivas som
**** Hänger inte riktigt med på denna biten.
Varför vill vi nu helt plötsligt skriva om det till d(phi)/d(t)?
Jag förstår att B blir kvar då magnetfältet från permanentmagneten är konstant. Nu blir d(A)/d(t) derivatan, men förstår inte varför och hur detta ses.
I figuren är det alltså när byter tecken, som gör att byter tecken (dvs byter polaritet).
Den mot magnetfältet vinkelräta inneslutna arean är maximal när slingan befinner sig i horisontalplanet i figuren vilket betyder att just i det ögonblicket byter tecken.
(bild)
Hänger med på att det nu beror på när d(A)/d(t) byter tecken som medför att e (polariteten) byter tecken. Men vilken area är det egentligen?
Förstår att den är maximal när den är i horisontalplanet då den blir vinkelrät mot magnetfältet.
Egentligen frågorna som återstår nu:
1. Vilken area räknar man med?
2. Är det för varje gång när ledaren/slingan hamnar vinkelrätt det byter tecken då det uppnår sitt maxvärde?
3. Varför vill man skriva om det till d(phi)/d(t)?
4. Vart exakt är det d(A)/d(t) har sin "roll"?
Vilka bra frågor!
1. Vilken area räknar man med?
Ledarslingan bildar en loop som innesluter en area. Projiceringen av denna inneslutna area i planet som är vinkelrätt mot magnetfältet är den area som räknas (dvs horisontalplanet, om magnetfätet är riktat vertikaltsom i din figur) . Denna projicerade area kommer att variera med tiden eftersom ledarslingan roterar. När ledarslingan pekar vertikalt:
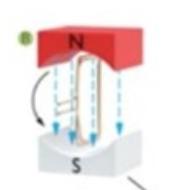
Är arean som projiceras i horisontalplanet, noll. När ledarslingan pekar horisontellt:
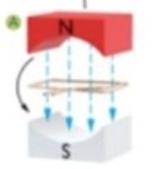
projiceras hela ledarslingans area i horisontalplanet, dvs arean blir maximal, vi kan kalla den .
Man kan visa med lite trigonometri, att den area som som projiceras i horisontalplanet beskrivs av
, med den tidsreferens som används i din figur. Dess tidsderivata blir då
Det är tidsberoendet i denna area som ger det varierande flödet som ger inducerad spänning enligt Faradays induktionslag
dvs den inducerade spänningen får formen av en sinusfunktion, precis som grafen i din figur visar.
2. Är det för varje gång när ledaren/slingan hamnar vinkelrätt det byter tecken då det uppnår sitt maxvärde?
När slingan är horisontell är arean maximal, men blir noll och byter tecken. När slingan är vertikal är arean A noll, men är maximal eller minimal.
3. Varför vill man skriva om det till d(phi)/d(t)?
Jag förstår inte riktigt vad du menar. Man vill beskriva genom ledarslingan eftersom Faraday (och Maxwell) kom fram till att det fungerar så.
4. Vart exakt är det d(A)/d(t) har sin "roll"?
Som jag försökte förklara i din fråga 1, den tidsvarierande arean är en förutsättning för att det ska induceras någon spänning. Om både magnetfältet och arean hade varit konstant så skulle också ha blivit konstant, och därmed ha blivit noll, och därmed blivit noll.
Men man hade kunnat inducerat en spänning i en ledarslinga likaväl genom att variera ett magnetfält genom en konstant area, det viktiga är att (där ) varierar. Ett sådant exempel är när man närmar sig med en stavmagnet mot en stillastående ledarslinga
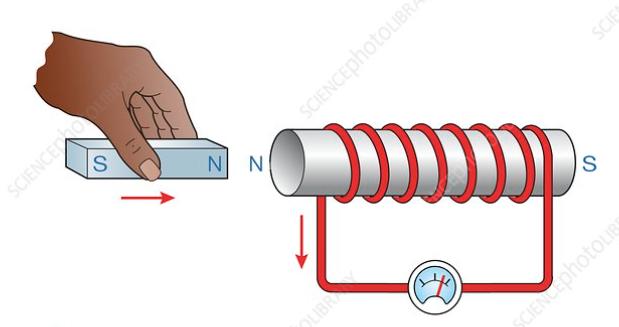
(det exemplet, eller liknande, har du säkert också sett i din lärobok).
Har läst detta men missat att tacka dig. Tack så mycket!


