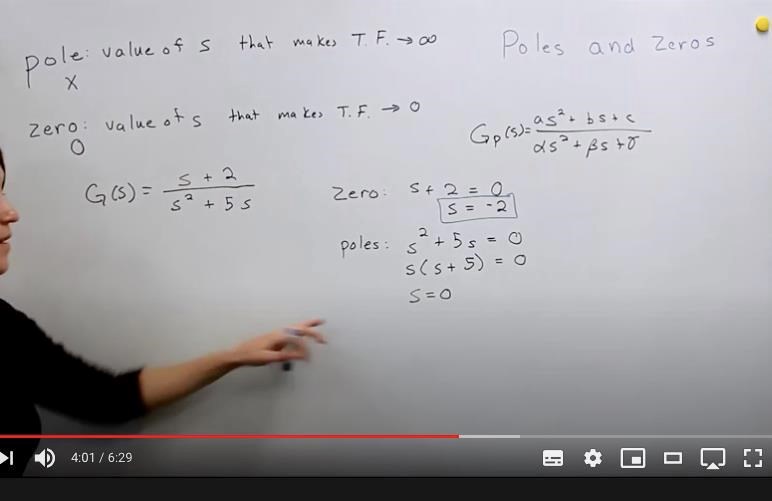
Poles och Zeros.

Ett nollställe betyder att funktionen blir 0, och en pol att du får delat på 0. Sen har en sjundegradare 7 lösningar, så ställ upp alla ekvationer i parenteserna och lös ordentligt (rita iaf). Sen kan det kanske hjälpa att taylorutveckla sin för att se vad som händer i +-1.

Hej,

Nollställen: Lösningar till ekvationen $z^5\sin \pi z = 0.$

Poler: Lösningar till ekvationen $(1-z^2)(2-z^2)(3-z^7)=0.$

Krav: Endast nollställen och poler som uppfyller olikheten $|z|<4.5$

Albiki skrev:

Hej,

Nollställen: Lösningar till ekvationen $z^5\sin \pi z = 0.$

Poler: Lösningar till ekvationen $(1-z^2)(2-z^2)(3-z^7)=0.$

Krav: Endast nollställen och poler som uppfyller olikheten $|z|<4.5$

Hej Alkibi!

• Nollställen: Med WA hjälp, så 2 st?
• Poler: Det är ju, nu körde jag WA lite snabbt, och då blir det allihop? dvs 5st?
  
  

Det du skriver, det är samma sak som denna va?

If 𝛼 is zero of order 𝑚 of 𝑓 and zero of order 𝑛 of 𝑔 and ℎ=𝑓/𝑔 then 𝛼xis (for function ℎ)

𝑖) removable singularity if 𝑚>𝑛. Here one can define ℎ(𝛼)=0 to "remove" the singularity and then 𝛼 becomes zero of order (𝑚−𝑛).

𝑖𝑖) pole of order (𝑛−𝑚) if 𝑛>𝑚.

𝑖𝑖𝑖) removable singularity if 𝑚=𝑛.

så mitt $m = 2$
$n = 5$

i ) $m>n \Rightarrow 2>5$ stämmer ej, så ingen 'removable' singularity?
ii) antal poler då $(n-m) \Rightarrow 5-2 = 3$
iii) ingen remobavble singuarity (igen?) för $5 \neq 2$.

Bump =)

Förstår inte alls vad du får 5 ifrån? Nämnaren är en 2+2+7=11-gradsfunktion och måste då ha 11 nollställen. Kan du se vad de har för belopp? Vilka ligger innanför cirkeln med radie 4,5?

Täljaren har dels 5 nollor i 0, från z^5, och minst ett till, eftersom sin 0 = 0. Vad har sinusfunktionen mer för nollställen?  Vilka ligger i cirkeln? Vet du hur man räknar ut multipliciteten för nollställena till sin?

Sen tror jag du har missat att en nolla/pol finns i en enda punkt. Du kan inte ta ut dem mot varandra om de inte ligger på samma ställe. I vilka punkter har du både och, alltså att både täljare och nämnare blir 0? Där kan du använda satsen med m-n och se ifall du får ett nollställe, en pol eller en hävbar singularitet.

Micimacko skrev:

Förstår inte alls vad du får 5 ifrån? Nämnaren är en 2+2+7=11-gradsfunktion och måste då ha 11 nollställen. Kan du se vad de har för belopp? Vilka ligger innanför cirkeln med radie 4,5?

Täljaren har dels 5 nollor i 0, från z^5, och minst ett till, eftersom sin 0 = 0. Vad har sinusfunktionen mer för nollställen?  Vilka ligger i cirkeln? Vet du hur man räknar ut multipliciteten för nollställena till sin?

Sen tror jag du har missat att en nolla/pol finns i en enda punkt. Du kan inte ta ut dem mot varandra om de inte ligger på samma ställe. I vilka punkter har du både och, alltså att både täljare och nämnare blir 0? Där kan du använda satsen med m-n och se ifall du får ett nollställe, en pol eller en hävbar singularitet.

• jag tänker såhär att när vår funktion f(z) går lim +/- 0, 1,2,3,4 så är de gränsvärdet 0, så dessa är då våra poler? dvs 10st.
• När både täljare och nämnare är 0, måste z=1, så de gör så att de inte är, varken zeroes nor poles. så från ovan, så är det 9 st? (10-1)
• Min femma kommer ifrån z^5 i täljaren
• men m-n satsen, så "alfa is zero fo orders m of f, and zero of there order n, of g, there h=f/g. Så då är m=5 n=11? neee :(

1) Rätt tänkt, men du räknade 0 två gånger ;) Och det är nollställen, för funktionen blir 0 där. En pol betyder att du har delat på 0.

2) z=1 är ena. z=-1 funkar också. Du får fortfarande inte blanda ihop grader i olika punkter. I 1 tex, så kan vi se direkt att 1 är en enkelrot till nämnaren, så vi har en enkelpol.

Vilken grad har nollstället? Du kan räkna ut det genom att derivera sin(piz) flera gånger, och för varje derivata som blir 0 när du stoppar in z=1 så ökar du m med 1. Tills du får en annan siffra.

4) Du får räkna ut för varje intressant punkt om det är nollställe eller pol, och i så fall av vilken grad, och sen räkna ihop hur många av varje det är totalt.

Micimacko skrev:

1) Rätt tänkt, men du räknade 0 två gånger ;) Och det är nollställen, för funktionen blir 0 där. En pol betyder att du har delat på 0.

2) z=1 är ena. z=-1 funkar också. Du får fortfarande inte blanda ihop grader i olika punkter. I 1 tex, så kan vi se direkt att 1 är en enkelrot till nämnaren, så vi har en enkelpol.

Vilken grad har nollstället? Du kan räkna ut det genom att derivera sin(piz) flera gånger, och för varje derivata som blir 0 när du stoppar in z=1 så ökar du m med 1. Tills du får en annan siffra.

4) Du får räkna ut för varje intressant punkt om det är nollställe eller pol, och i så fall av vilken grad, och sen räkna ihop hur många av varje det är totalt.

Okej, men om jag tittar på denna då (vi börjar om lite från början, för fattar inte vad det e jag får fel för)

• Min zero är z=1, och det är därför jag ska derivera $\sin^5 (\pi z)$ minst fem ggr och substituera in 1 i.  Då får jag ...
  
  första derivatan: 5 π cos(π z) sin^4(π z) , sub in z=1 ger: 0
  andra derivatan: -5 π^2 sin^3(π z) (-4 cos^2(π z) + sin^2(π z)) sub in z=1 ger: 0
  tredje derivatan: 5 π^3 cos(π z) sin^2(π z) (12 cos^2(π z) - 13 sin^2(π z)) sub in =1 : 0
  fjärde derivatan: 5 π^4 sin(π z) (24 cos^4(π z) - 88 cos^2(π z) sin^2(π z) + 13 sin^4(π z)) sub in z=1: 0
  femte derivatan: 5 π^4 sin(π z) (24 cos^4(π z) - 88 cos^2(π z) sin^2(π z) + 13 sin^4(π z))  sub in z=1: 0
  
  ger ju bara 0. Tyckte det där verkar lång sökt, kanske ska man använda MacLaurin istället vid z=1? eller hur? upp till typ "Olbe 7, typ den täljaren har grad 5? (vad heter den - har för mig att man säger Olbe, eller ja du vet nog vad jag menar ^^^) 
• polerna är $0, \pm 1,2,3,4$ dvs 9 stycken, inuti disken 4.5?

Kolla på din funktion. Var har du sin upphöjt till 5? Man kan utveckla, men du kommer inte behöva det här.

Varför kallar du 0,1,2.. för poler?

En McLaurinutveckling måste vara runt 0,annars är det en taylorutveckling. Och resttermen brukar kallas för ordo. Om man ska vara petig ;P

Micimacko skrev:

Kolla på din funktion. Var har du sin upphöjt till 5? Man kan utveckla, men du kommer inte behöva det här.

Varför kallar du 0,1,2.. för poler?

En McLaurinutveckling måste vara runt 0,annars är det en taylorutveckling. Och resttermen brukar kallas för ordo. Om man ska vara petig ;P

Mkt sant, det är z^5 inte sin^5?

men vad som man kalla det annars?

jaaa ordo, fick jag olbe ifrån? Hmm

Kalla det typ nollställen?

Vad fick du för grad på nollställena i sin nu? Och hur många nollställen och poler har du då totalt i z=1 och z=-1?

Micimacko skrev:

Kalla det typ nollställen?

Vad fick du för grad på nollställena i sin nu? Och hur många nollställen och poler har du då totalt i z=1 och z=-1?

Jag tänkte såhär... täljaren har grad 5, nämnaren har grad 28. men eftersom vi inte får räkna med \pm 1 ,så tänker jag att det  man "tänker bort" hela den parentesen, alltså har vi bara 7+2=9eller? tänker jag rätt nu?

Sedan läser jag detta:

Men vet inte..? känner mig inte helt 100 med den här lösningen

 1.  Bestäm vilken punkt du tittar på FÖRST, sen kan du börja räkna grader just I den punkten.

2. 28??

Micimacko skrev:

 1.  Bestäm vilken punkt du tittar på FÖRST, sen kan du börja räkna grader just I den punkten.

2. 28??

asså fattar iiingenting.. blir ju bara grötit

Jag försökte hitta på ett lite enklare exempel och förklara stegen. Hänger du med här?