Polynomdivision liggande stolen
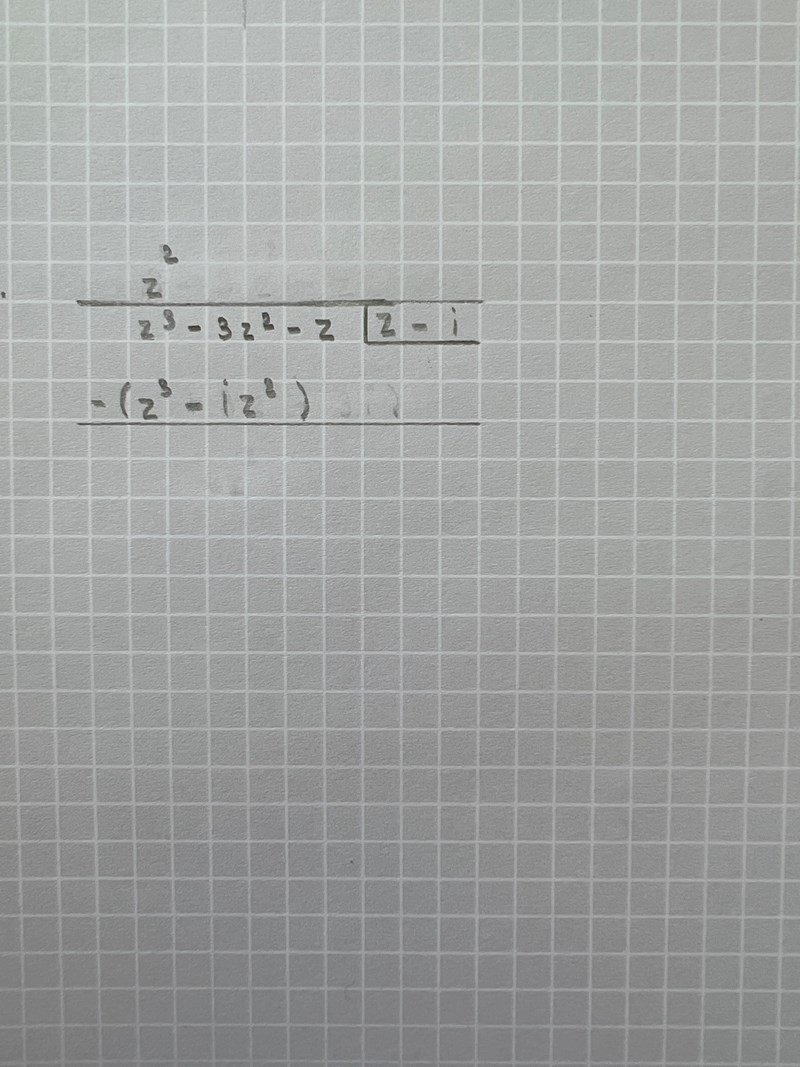 behöver hjälp att komma vidare till nästa steg!
behöver hjälp att komma vidare till nästa steg!
Om en polynom har en komplex rot kommer des konjugat också vara en rot. Med hjälp av det kan du hitta ett bättre uttryck att bryta ut.
ItzErre skrev:Om en polynom har en komplex rot kommer des konjugat också vara en rot. Med hjälp av det kan du hitta ett bättre uttryck att bryta ut.
Okej så om jag ska ta reda på resten är det bättre att ta reda på det så finns det bättre sätt än liggande stolen?
Nej liggande stolen ska du använda, jag menar att det finns en bättre faktor att bryta ut än z-i
(z-i)3 z3-iz3.
Visa spoiler
Skriv ditt dolda innehåll här
Ska jag använda mig av liggande stolen eller finns det något enklare sätt att få ut resten?
Liggande stolen är bäst, men multiplicera ihop (z-1)(z+1) istället för att behöva göra två "liggande stolen".
Smaragdalena skrev:Liggande stolen är bäst, men multiplicera ihop (z-1)(z+1) istället för att behöva göra två "liggande stolen".
När menar du att jag ska multiplicera ihop dessa?
Vad är (z-i)(z+i)?
ItzErre skrev:Vad är (z-i)(z+i)?
z^2+zi -zi-i^2 = z^2-i^2
Nath skrev:ItzErre skrev:Vad är (z-i)(z+i)?
z^2+zi -zi-i^2 = z^2-i^2
Ja, det stämmer att (z-i)(z+i) = z2-i2, men du kan förenkla lite till. Vad är i2?
Smaragdalena skrev:Nath skrev:ItzErre skrev:Vad är (z-i)(z+i)?
z^2+zi -zi-i^2 = z^2-i^2
Ja, det stämmer att (z-i)(z+i) = z2-i2, men du kan förenkla lite till. Vad är i2?
z^2-1
Nu verkar du svara till hälften på den ena och till hälften på den andra av de båda frågorna.
i2 = -1.
z2-i2 = z2-(-1) = ...
Smaragdalena skrev:Nu verkar du svara till hälften på den ena och till hälften på den andra av de båda frågorna.
i2 = -1.
z2-i2 = z2-(-1) = ...
Just det, svarade för fort. Men hur hjälper detta mig förstår inte vilket steg jag räknar på
Vad skall nämnaren vara i din polynomdivision?
Vad är uppgiften?
Varför ska du dividera?
Ture skrev:Vad är uppgiften?
Varför ska du dividera?
Jag ska ta reda på resten när z^3-3z^2-z divideras med z-i
Nath skrev:Ture skrev:Vad är uppgiften?
Varför ska du dividera?
Jag ska ta reda på resten när z^3-3z^2-z divideras med z-i
Skall du inte faktorisera z3-3z2-z? Fast det är klart, så skulle du ha börjat med att bryta ut z så att du fick z(z2-3z-1) och så hade du använt pq-formeln och fått fram z(z-5)(z+2).
Jag trillade i gropen som ItzErre hade grävt.
Då går vi tillbaka till din första bild. z3-z3 = 0, 0-(-iz2 )= iz2, så hela nästa rad blir -3z2+iz2-z. Nästa term i kvoten blir -3z.
Smaragdalena skrev:Nath skrev:Ture skrev:Vad är uppgiften?
Varför ska du dividera?
Jag ska ta reda på resten när z^3-3z^2-z divideras med z-i
Skall du inte faktorisera z3-3z2-z? Fast det är klart, så skulle du ha börjat med att bryta ut z så att du fick z(z2-3z-1) och så hade du använt pq-formeln och fått fram z(z-5)(z+2).
Jag trillade i gropen som ItzErre hade grävt.
Då går vi tillbaka till din första bild. z3-z3 = 0, 0-(-iz2 )= iz2, så hela nästa rad blir -3z2+iz2-z. Nästa term i kvoten blir -3z.
 ser det okej ut hittils eller är det något jag har missat?
ser det okej ut hittils eller är det något jag har missat?
Rätt så långt!
Ture skrev:Rätt så långt!
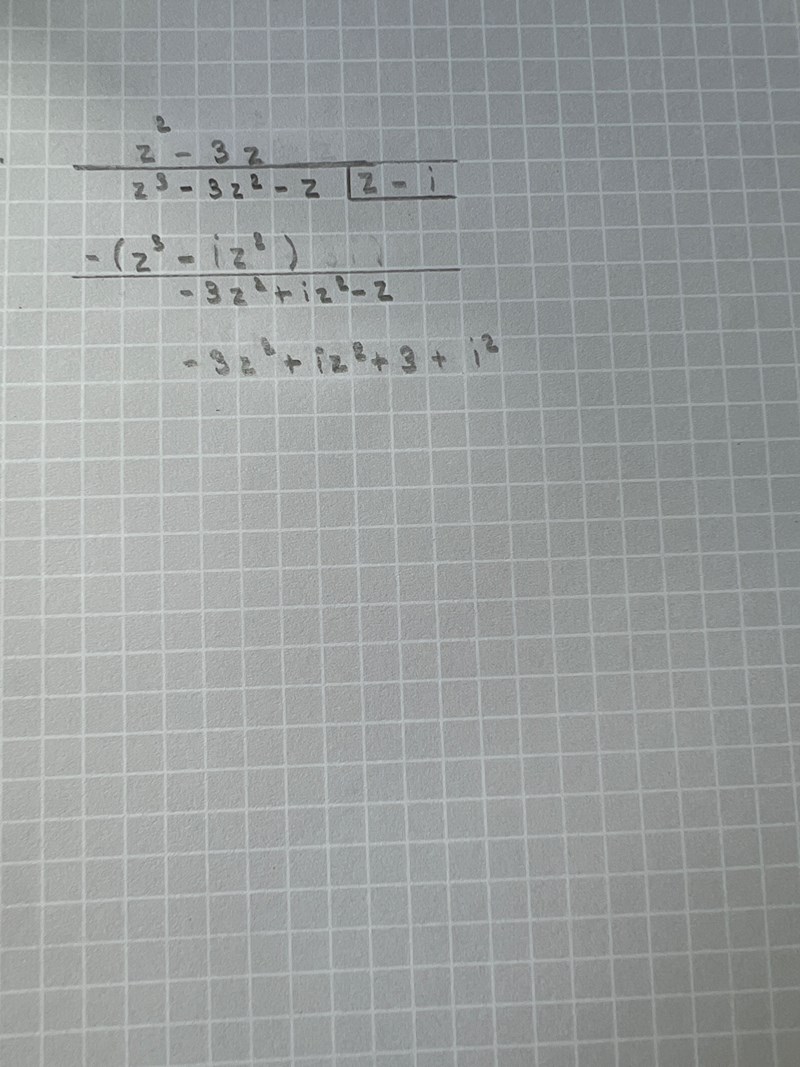 Kommer inte framåt, gärna mer hjälp, rör ihop det med i och z i samma…
Kommer inte framåt, gärna mer hjälp, rör ihop det med i och z i samma…
Sudda sista raden skriv istället in vad
-3z * (z-i) blir
Ture skrev:Sudda sista raden skriv istället in vad
-3z * (z-i) blir
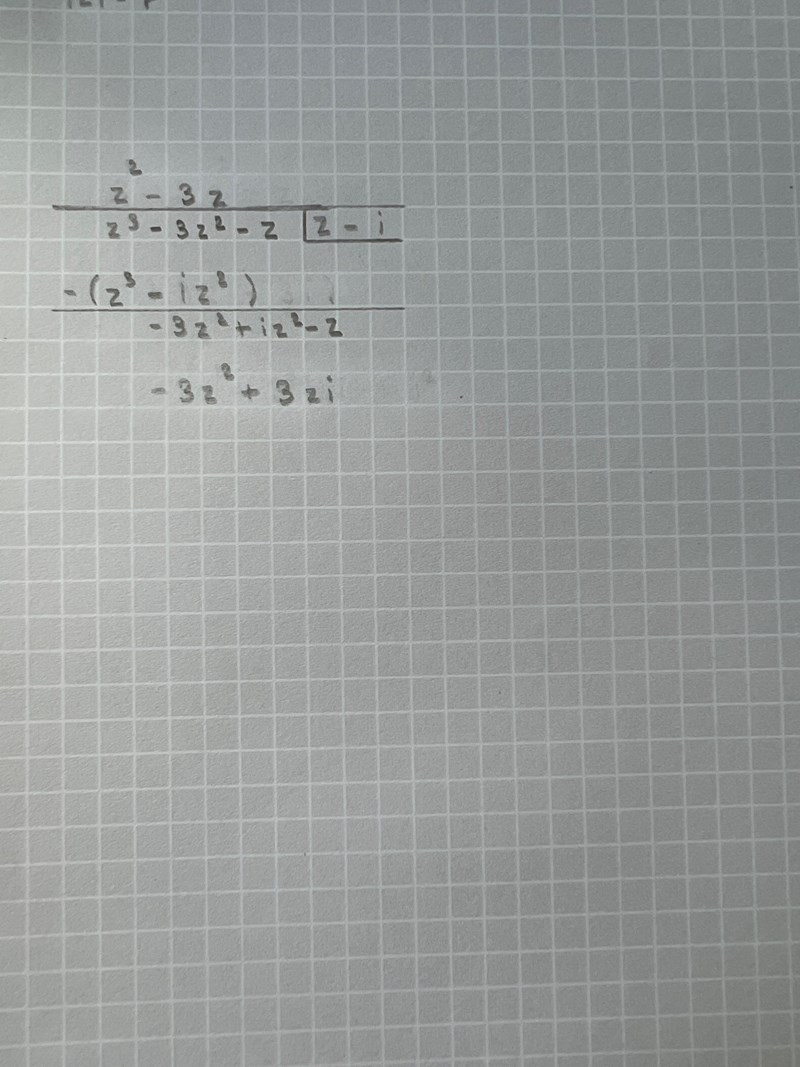 så?
så?
just så, sen ändrar du tecken på sista raden (precis som du gjorde på rad 2) och summerar raden ovanför (som du gjorde på rad 3)
Ture skrev:just så, sen ändrar du tecken på sista raden (precis som du gjorde på rad 2) och summerar raden ovanför (som du gjorde på rad 3)
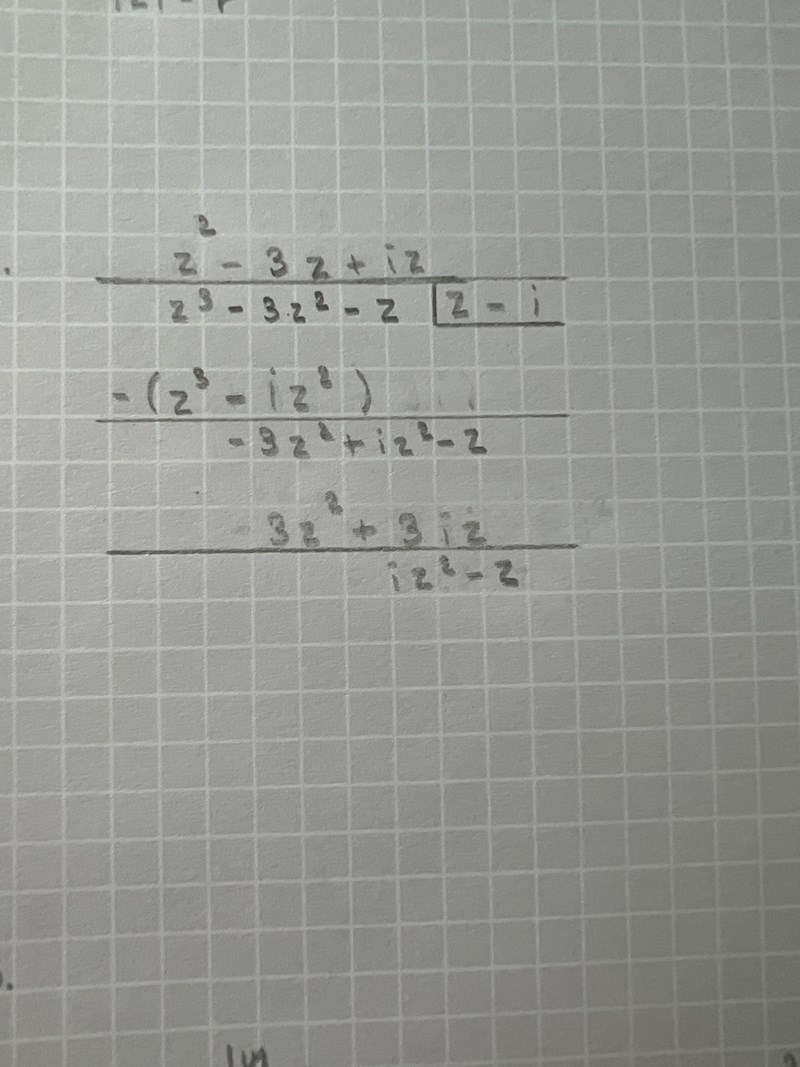
osäker på hur följande blir, uppskattar ännu mer hjälp
jag klantade till det en bit upp, om du har lust får vi backa bandet, från första inlägget.
läs nästa inlägg som jag skriver om en liten stund..
Ture skrev:jag klantade till det en bit upp, om du har lust får vi backa bandet, från första inlägget.
läs nästa inlägg som jag skriver om en liten stund..
Okej!
Nath skrev:
behöver hjälp att komma vidare till nästa steg!
om du summer det du har får du på nästa rad
-3z2 + iz2 -z
jag missade att vi nu måste skriva om uttrycket ovan till
z2(-3+i) -z
Nu kan vi hitta andra termen i din kvot, den blir z*(-3+i)
Ture skrev:Nath skrev:
behöver hjälp att komma vidare till nästa steg!
om du summer det du har får du på nästa rad
-3z2 + iz2 -z
jag missade att vi nu måste skriva om uttrycket ovan till
z2(-3+i) -z
Nu kan vi hitta andra termen i din kvot, den blir z*(-3+i)
 Har jag missat något?
Har jag missat något?
ja, i kvoten ska det inte stå -3z utan det ska stå
+ z(-3+i)
Ture skrev:ja, i kvoten ska det inte stå -3z utan det ska stå
+ z(-3+i)
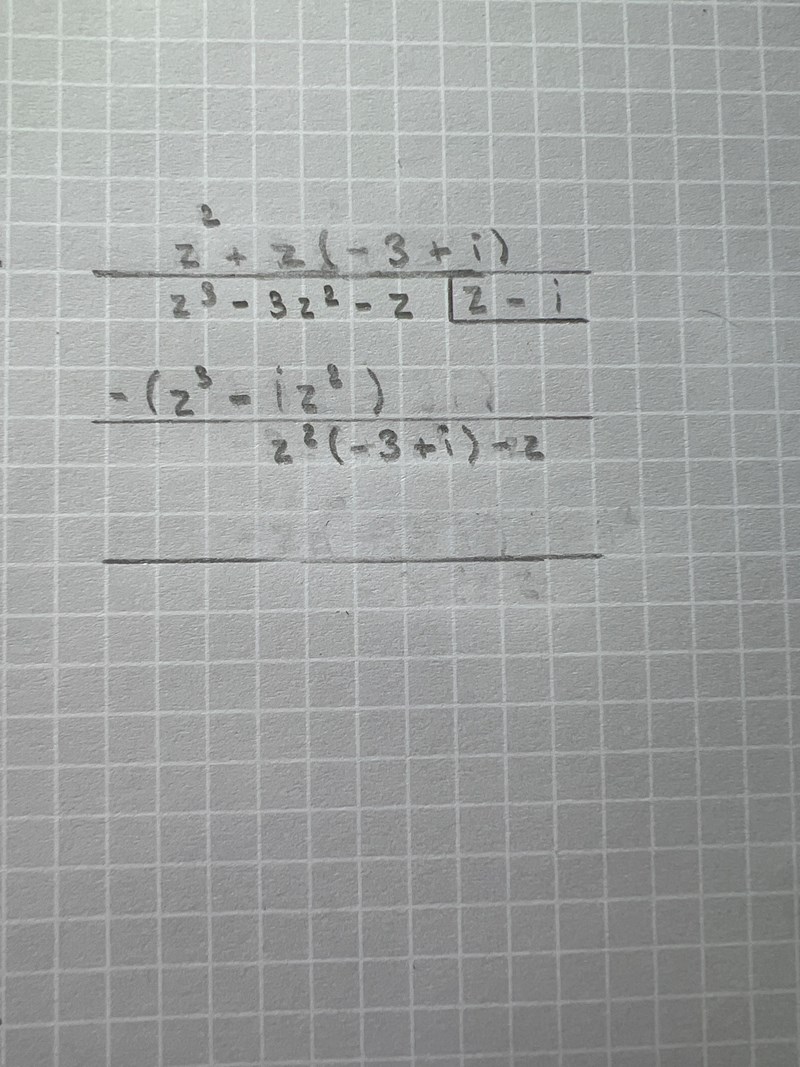
Eftersom det blev så trassligt har jag lagt in en lösning nedan
Fråga om det du inte förstår.
Resten är nästan det som står på sista raden, där har jag gjort ett teckenfel, ska vara 3-2i.

Ture skrev:Eftersom det blev så trassligt har jag lagt in en lösning nedan
Fråga om det du inte förstår.
Resten är nästan det som står på sista raden, där har jag gjort ett teckenfel, ska vara 3-2i.
Tack så mycket!
Kvoten
(z^3 -3 z2 -z )/(z-i) = z2 +z(-3+i) +(-2-3i) + (3-2i)/(z-i)




