Polynomekvationer

Hej

Jag har fastnat på en fråga i min uppgift och förstår inte riktigt vad som blir fel. Jag har försökt lösa den och försökt på 2 olika sätt men frågar jag personer runt mig så är båda fel och dem tror att ekvationen är fel från början att det ska vara +36 istället för -36.

Lös ekvationen:

$x^{4} - 13 x^{2} - 36 = 0$

Jag har löst den på detta sätt:

$x^{4} - 13 x^{2} = 36 x^{2} (x^{2} - 13) = 36 x^{2} = \pm \sqrt{36} x = \pm 6 x^{2} - 13 = 36 x^{2} = 36 + 13 x^{2} = 49 x = \pm \sqrt{49} x = \pm 7 S v a r : x = \pm 6 o c h x = \pm 7$

Och på detta sätt: (denna tror jag garanterat är fel eftersom att något upphöjt i 36 blir extremt stort)

$x (x^{3} - 13 x) - 36 = 0 x = 0 x^{3} - 13 x - 36 = 0 x^{3} - 13 x = 36 x (x^{2} - 13) = 36 x = 36 x^{2} - 13 = 36 x^{2} = 36 + 13 x^{2} = 49 x = \pm \sqrt{49} x = \pm 7 S v a r : x = 0 o c h x = 36 o c h x = \pm 7$

Tacksam för svar snabbt :)

Enklast är nog att tillfälligt kalla x² för t

då får vi

t² -13t -36 = 0

som du kan lösa med pq formeln eller kvadratkomplettering

nör du vet vad t kan vara är det sen enkelt att bestämma x

Det är förvisso sant att det blir snyggare lösningar om det står +36 i stället.

menar du såhär? Det känns jätte fel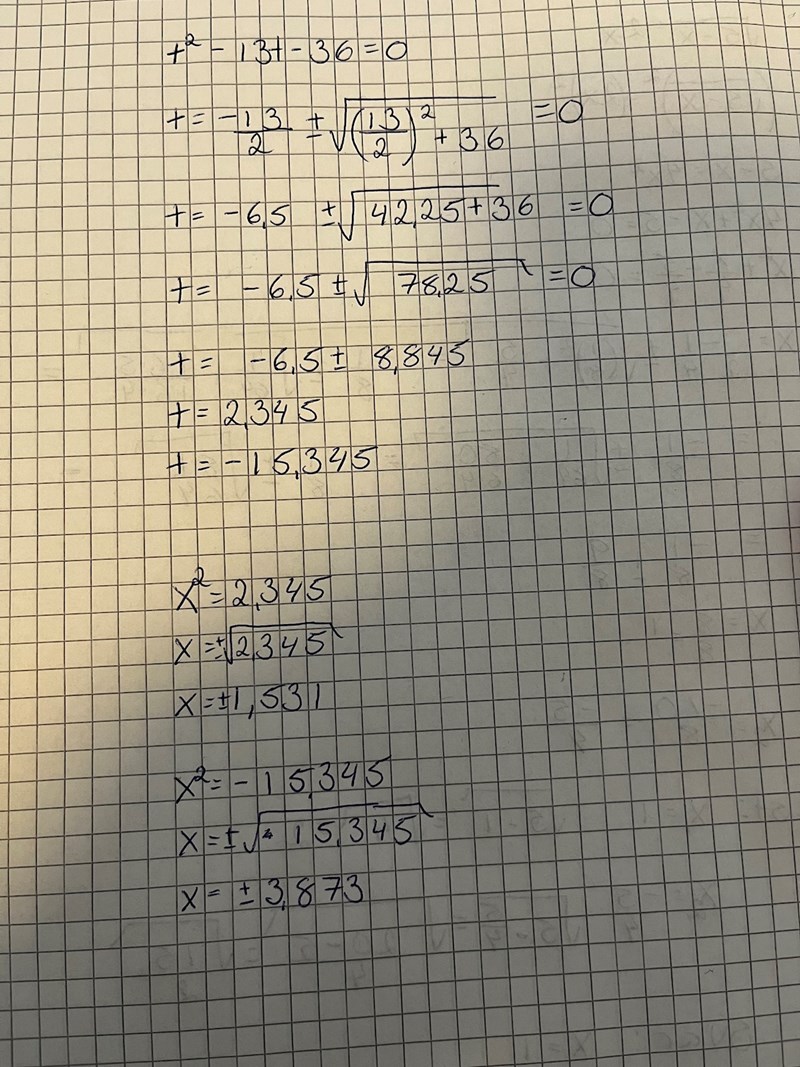

Ture skrev:
Enklast är nog att tillfälligt kalla x² för t

då får vi

t² -13t -36 = 0

som du kan lösa med pq formeln eller kvadratkomplettering

nör du vet vad t kan vara är det sen enkelt att bestämma x

menar du såhär? Det känns jätte fel

Här ör två fel (se bild)

Det ska vara ett plustecken framför termen $\frac{13}{2}$ . Detta eftersom första termen I pq-formeln är $-\frac{p}{2}$ och $p$ I detta fallet är -13.
Det ska inte stå "=0" till höger.

blir det så här då?

Nej inte riktigt.

Till att börja med ska du inte avrunda, se dock nedan.

Sedan tappar du bort ett minustecken här:

Om $x^2=-2,345$ så är $x=\pm\sqrt{-2,345}$ , vilket ger två komplexa lösningar.

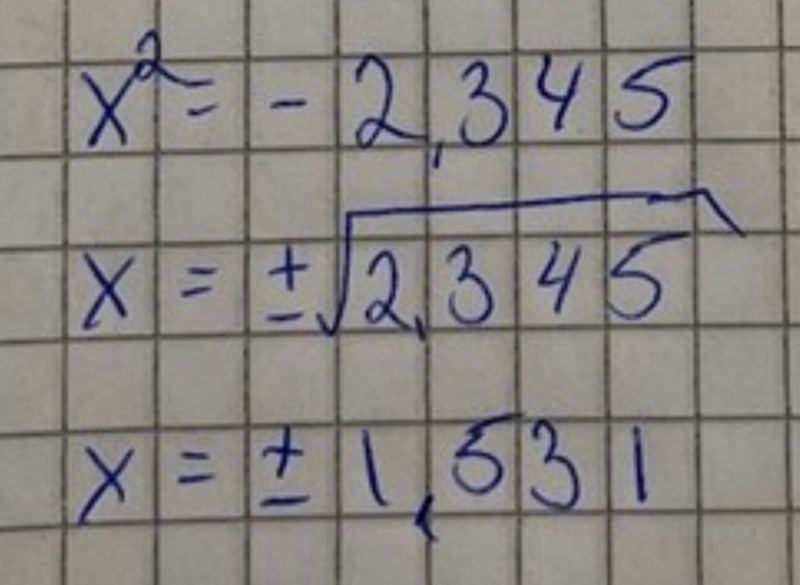
===== Nedan =====

De fyra lösningarna blir onödigt trassliga. Jag tror samma sak som flera andra här, att ekvationen som ska lösas istället är x⁴-13x²+36 = 0. Då behöver du inte avrunda.

Ge dig på att lösa den med samma metod som du redan ör inne på, dvs att substituera x² med t.

Okej tack har frågat läraren om det ska vara +36 men inte fått något svar. Men skriver man in +- roten ur -2,345 står det fel i miniräknaren att det inte går att räkna ut på miniräknare.

Linnea9808 skrev:
Okej tack har frågat läraren om det ska vara +36 men inte fått något svar.

OK bra. Men lös istället ekvationen x⁴-13x²+36 = 0 i väntan på svar. Visa din lösning.

Men skriver man in +- roten ur -2,345 står det fel i miniräknaren att det inte går att räkna ut på miniräknare.

Det är för att roten ur ett negativt tal blir ett s.k. komplext tal och din räknare kan nog inte visa det.

Komplexa tal introduceras först i Matte 4, vilket tyder på att den givna ekvationen inte är rätt.

såhär?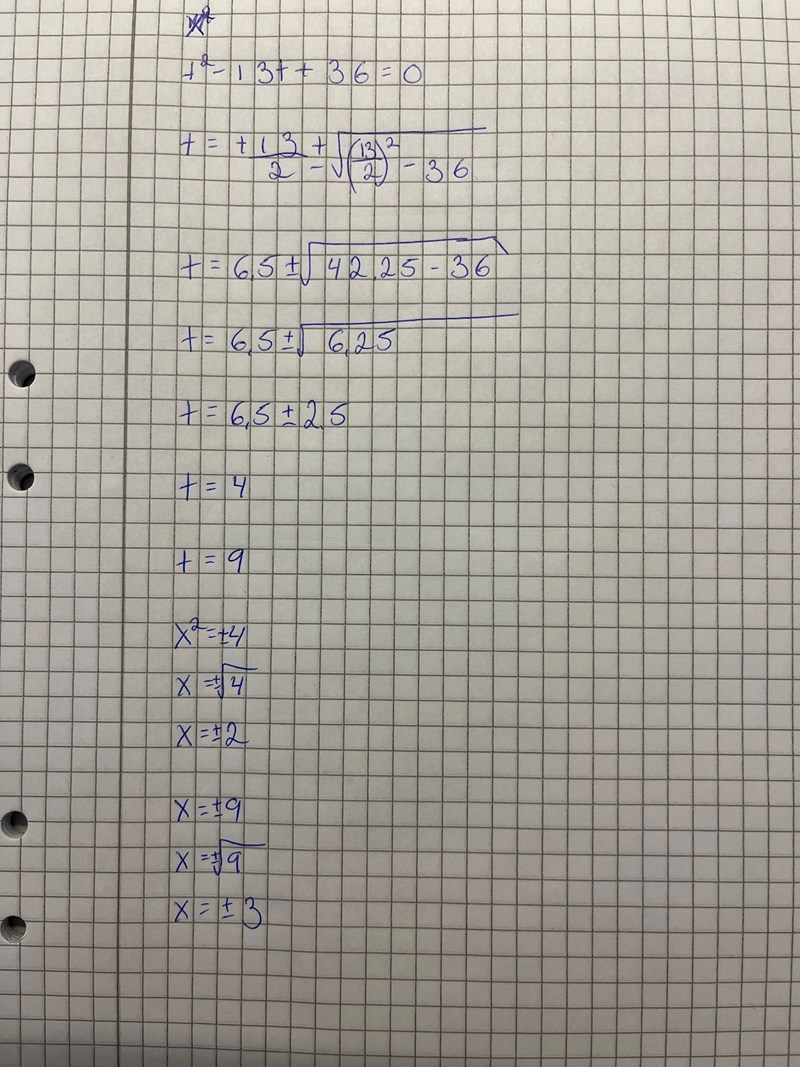

Nästan.

Allt är rätt förutom de två gulmarkerade.

Eftersom $x^2=t$ och $t=4$ så gäller det att $x^2=4$ , inte $x^2=\pm4$

Samma sak lite längre ner, det ska stå $x^2=9$

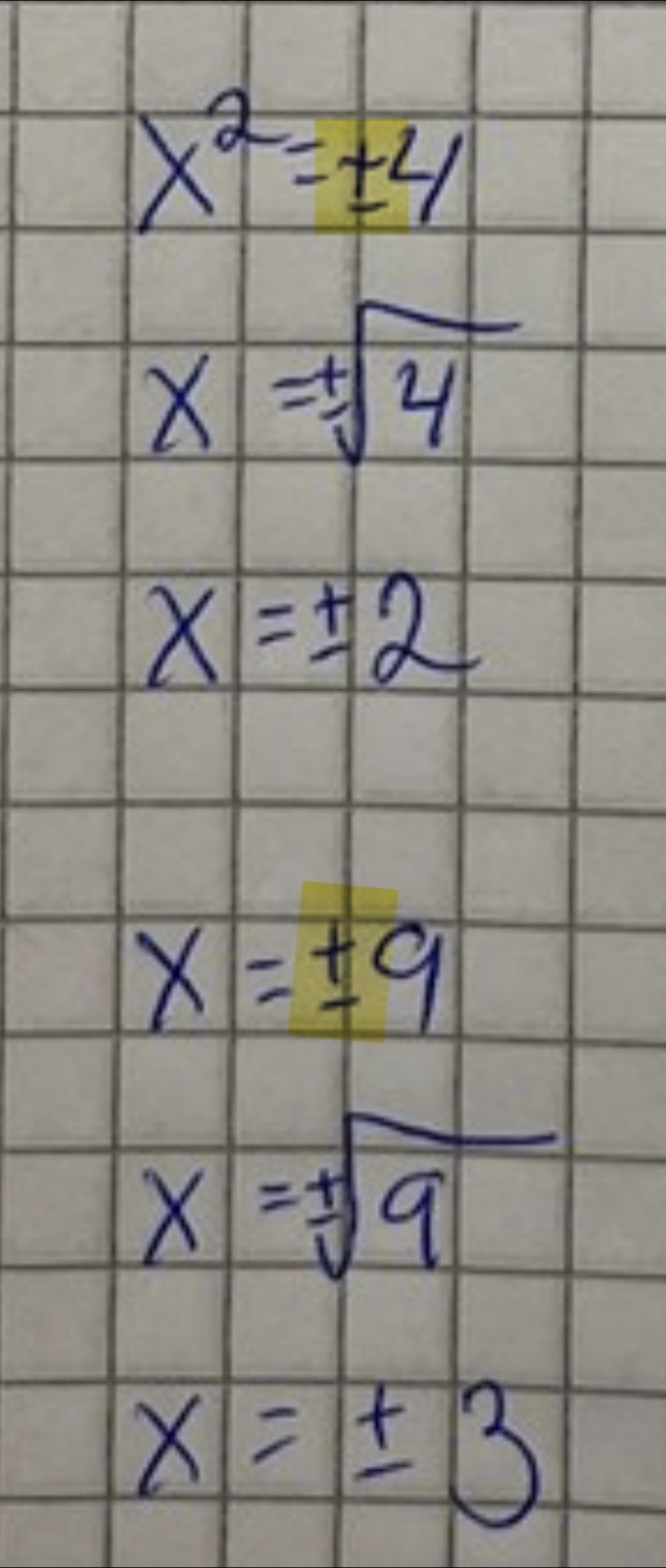
Oj blev lite fel gick lite snabbt på slutet av ekvationen men Tack så mycket för hjälpen :)

Svara

Visa senaste svar