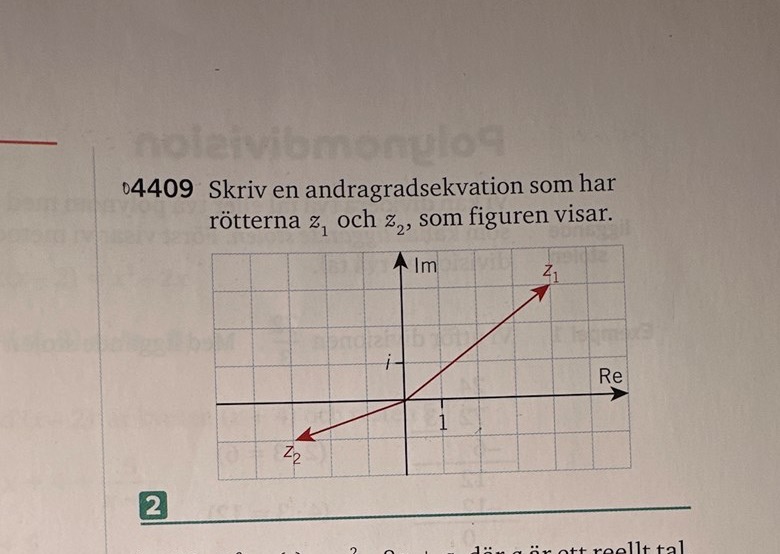
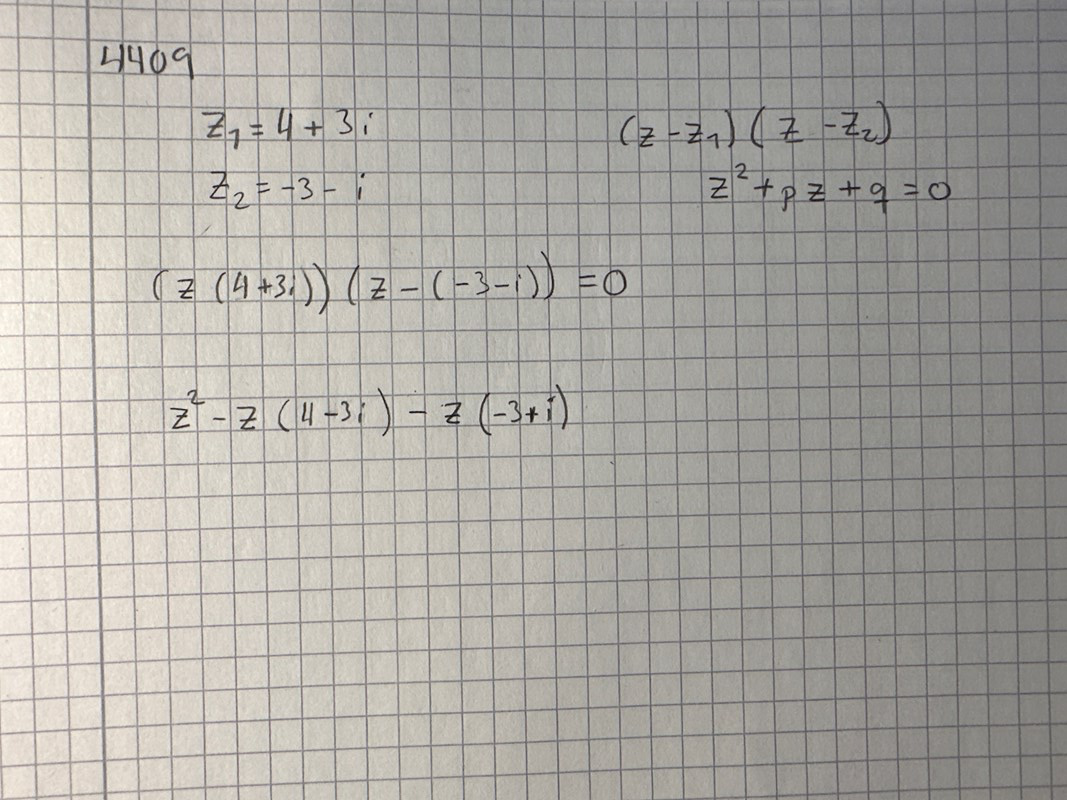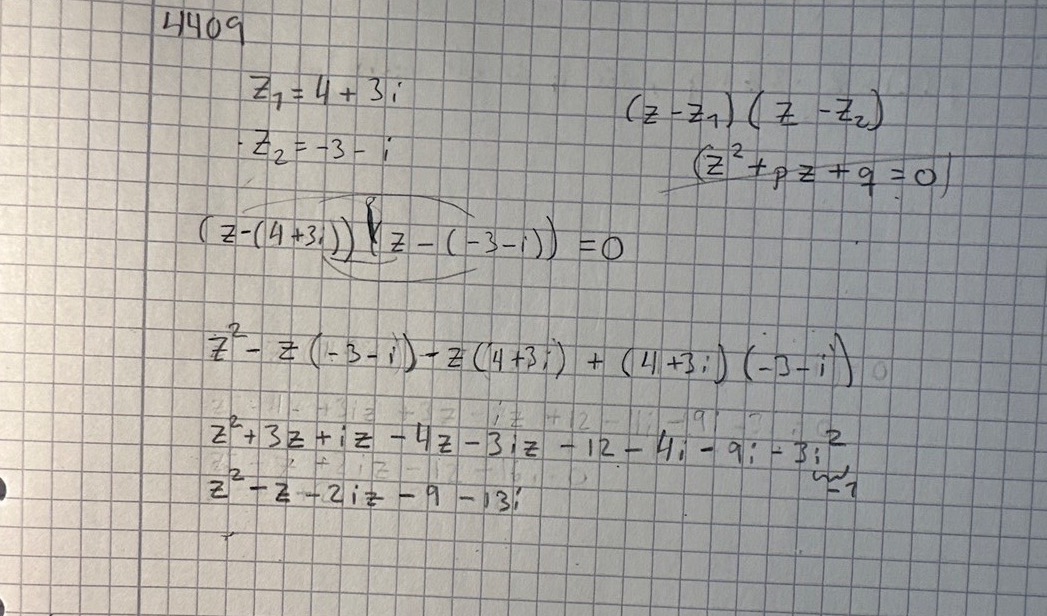Polynomekvationer rötter
 Hejsan
Hejsan
Jag har läst av i Talplanet.
z=4+3i
z=-3-i
men kan inte riktigt se hur och varför man kan beräkna som i exemplet nedan.

Hej!
Rötterna är lösningen till ekvationen VL=HL
Om HL är 0, så måste vi konstruera ett VL som också blir noll ifall roten stoppas in.
Och för att VL ska bli noll så räcker det med att en av faktorerna i VL blir noll.
Hänger du med?

”konstruera ett VL som också blir noll” är det med hjälp av båda rötterna?
”konstruera ett VL som också blir noll” är det med hjälp av båda rötterna?
Ja, eftersom du vill att båda rötterna ska ge VL=0.
Hänger du med?
Ja, och därav används formen (z-z1)(z-z2) ?
jag tolkade exemplet 4402 som att rötterna måste vara komplexa konjugerande tal för att använda formen (z-z1)(z-z2)
Hur menar du?
Biorr skrev:Ja, och därav används formen (z-z1)(z-z2) ?
jag tolkade exemplet 4402 som att rötterna måste vara komplexa konjugerande tal för att använda formen (z-z1)(z-z2)
Aha, då förstår jag varför du blir förvirrad! Nä, den där metoden är generell för alla typer av tal.
Enda villkoret som ställs på för att , är ju att eller .
Det behöver inte ställas några krav på och .