Pos definit/indefinit

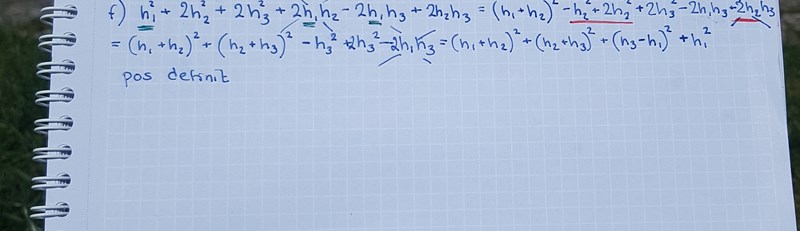
Du tänker helt rätt, men du gör rätt många steg på samma gång i dina beräkningar, och då är det väldigt lätt att göra fel om man inte har en Ti-84:a till hjärna. Dessutom blir det svårare att gå tillbaka och upptäcka slarvfel i efterhand. Så mitt tips är att ta det lugnare framöver och inte vara rädd för att skriva ut fler mellanled.

Jag får det till att det kvadratiska formen blir

  $Q(h_1,h_2,h_3)=h_1^2 + 2h_2^2 + 2h_3^2 + 2h_1h_2 - 2h_1h_3 + 2h_2h_3\\\quad =(h_1+h_2)^2 + h_2^2 + 2h_3^2 - 2h_1h_3 + 2h_2h_3\\\quad =(h_1+h_2)^2 + (h_2+h_3)^2 + h_3^2 - 2h_1h_3\\\quad =(h_1+h_2)^2 + (h_2+h_3)^2 + h_3^2 - 2h_1h_3+h_1^2-h_1^2\\\quad =(h_1+h_2)^2 + (h_2+h_3)^2 + (h_3-h_1)^2 - h_1^2\,,$

och utifrån detta är det relativt enkelt att se att $Q$ kan anta både positiva och negativa värden.

Kan du ge några exempel? :)

oggih skrev:

Du tänker helt rätt, men du gör rätt många steg på samma gång i dina beräkningar, och då är det väldigt lätt att göra fel om man inte har en Ti-84:a till hjärna. Dessutom blir det svårare att gå tillbaka och upptäcka slarvfel i efterhand. Så mitt tips är att ta det lugnare framöver och inte vara rädd för att skriva ut fler mellanled.

Jag får det till att det kvadratiska formen blir

   $Q(h_1,h_2,h_3)=h_1^2 + 2h_2^2 + 2h_3^2 + 2h_1h_2 - 2h_1h_3 + 2h_2h_3\\<br />=(h_1+h_2)^2 + h_2^2 + 2h_3^2 - 2h_1h_3 + 2h_2h_3\\<br />=(h_1+h_2)^2 + (h_2+h_3)^2 + h_3^2 - 2h_1h_3\\<br />=(h_1+h_2)^2 + (h_2+h_3)^2 + (h_3-h_1)^2 - h_1^2\\<br />(h_1+h_2)^2 + (h_2+h_3)^2 + (h_3-h_1)^2 - h_1^2\,,$

och utifrån detta är det relativt enkelt att se att $Q$ kan anta både positva och negativa värden. Kan du ge några exempel? 

Tack för svar! Jo om h1^2 ska vara negativ är det lätt att föstå. Det får ju ändå bli en följdfråga då, om den hade varit positivt som jag fick den till att bli, hade den då varit positivt definit? Eller måste det vara 3 kvadreringar enkom? Är de bara två är den ju semidefinit.

Bra fråga!

Det korta svaret är att man inte utan vidare bara kan räkna termer för att skilja positivt definita och positivt semidefinita kvadratiska former åt, utan man måste kolla lite närmare på vad som står innanför kvadraterna i kvadratkompletteringen.

Exempel 1: Den kvadratiska formen som du råkade få fram (fast med $x,y,z$ som varaibler i stället för $h_1,h_2,h_3$):

   $Q(x,y,z)=(x+y)^2+(y+z)^2+(z-x)^2+x^2$

är positivt definit, eftersom $Q\geqslant 0$ (det är en summa av kvadrater med positiva koefficienter), med likhet om och endast om det som står innanför kvadraterna är 0, vilket ger systemet

$\left\{\begin{array}{l}x=0\\z-x=0\\y+z=0\\x+y=0\end{array}\right.$

som enbart har lösningen $x=y=z=0$.

Exempel 2: Om vi i stället betraktar följande summa av kvadrater:

   $Q(x,y,z)=(x+y)^2+(x-y)^2+(x-2y)^2+(x-3y)^2\,,$

så kommer den vara positivt semidefinit. Av samma skäl som tidigare är $Q\geqslant 0$, med likhet om och endast om

   $\left\{\begin{array}{l}x+y=0\\ x-y=0\\ x-2y=0\\ x-3y=0\,.\end{array}\right.$

Detta system har oändligt många lösningar! Det är lätt att se att $x=y=0$ måste gälla, men $z$ kan vara vad tusan som helst (eftersom $z$ inte ens förekommer i systemet)! Så den här kvadratiska formen är positivt semidefinit.

Generellt: Antag att vi har en kvadratisk form $Q(x,y,z)$ som vi har kvadratkompetterat så att den står på formen

   $Q(x,y,z)=\alpha_1(\square)^2+\cdots+\alpha_m(\square)^2\,,$

med positiva koefficienter $\alpha_1,\ldots,\alpha_m>0$. Då kommer $Q\geqslant 0$ gälla, så $Q$ är antingen positivt definit eller positivt semidefinit. Det som är avgörande är om ekvationssystemet

   $\left\{\begin{array}{l}\square=0\\ \square=0\\ \vdots \\ \square=0\,.\end{array}\right.$

(som erhålls när vi sätter uttrycken innanför kvadraterna lika med 0) har någon icke-trivial lösning.

Om $m<3$ (t.ex. om $m=2$) så kommer systemet vara underbestämt, och då finns det garanterat icke-triviala lösningar, så $Q$ kommer vara positivt semidefinit, precis som du säger!

Men om $m\geqslant 3$ så går det inte att omedelbart dra någon slutsats, utan vi måste titta närmare på ekvationssystemet. Mer precist så handlar det om hur många linjärt oberoende rader det finns i systemet:

• Om det finns tre stycken linjärt obereonde rader så kommer systemet bara ha lösningen $x=y=z=0$, och $Q$ kommer vara positivt definit.
• Om det finns färre än tre linjärt oberoende rader så kommer systemet ha icke-triviala lösningar, och $Q$ kommer vara positivt semidefinit.

Det som jag skrev i inlägget här ovan går förstås att generalisera till godtyckliga kvadratiska former $Q(x_1,\ldots,x_n)$ i $n$ stycken variabler. Dessutom finns det ett litet algebraiskt trick som kan vara värt att känna till, om man tycker det här med att hålla på med ekvationssystem och räkna linjärt oberoende ekvationer är jobbigt. 

Om man kvadratkompletterar "smart" (t.ex. med hjälp av något som kallas för ortogonal diagonalisering av symmetriska matriser, vilket du kanske redan har stött på, eller kommer att stöta på, om du läser en kurs i linjär algebra), så kan varje kvadratisk form $Q(x_1,\ldots,x_n)$ i $n$ stycken variabler skrivas som en linjärkombination av $n$ stycken kvadrater

    $Q(x_1,\ldots, x_n)=\lambda_1 (\square)^2+\cdots+\lambda_n (\square)^2\,,$

där $\lambda_1,\ldots,\lambda_n\in\mathbb{R}$ och det som står innanför kvadraterna är $n$ stycken linjärt oberoende uttryck i variablerna $x_1,\ldots,x_n$.

Om man har lyckats skriva $Q$ på den här formen, med linjärt oberoende uttryck innanför kvadraterna, och om alla koefficienter är större än eller lika med 0, så vet vi (återigen) att $Q\geqslant 0$, dvs. $Q$ är antingen positvt definit eller positivt semidefinit.

Och nu kommer det fina i kråksången: vet vi att det som står innanför kvadraterna är linjärt oberoende uttryck så behöver vi inte bekymra oss om koefficienterna. Mer precist gäller att

• $Q$ är positivt definit om alla koefficiter är nollskilda.
• $Q$ är positivt semidefinit om någon av koefficienterna är noll.

I just ditt fall med $Q=(x+y)^2+(y+z)^2+(z-x)^2+x^2$ så avslöjar diagonaliseringstricket (här kan du se vad jag bad WolframAlpha att göra) att vi kan skriva $Q$ på formen

   $Q(x,y,z)=3(\square)^2+(2-\sqrt{3})(\square)^2+(2+\sqrt{3})^2(\square)^2\,.$

Uttrycken innanför parenteserna kommer vara fruktansvärt fula och lite småjobbiga att räkna fram, men metoden garanterar att de kommer vara linjärt oberoende, så vi behöver inte bekymra oss om exakt vad de är. Eftersom koefficienterna är strikt positiva så kan vi direkt dra slutsatsen att $Q$ är positivt definit.