Potensekvation
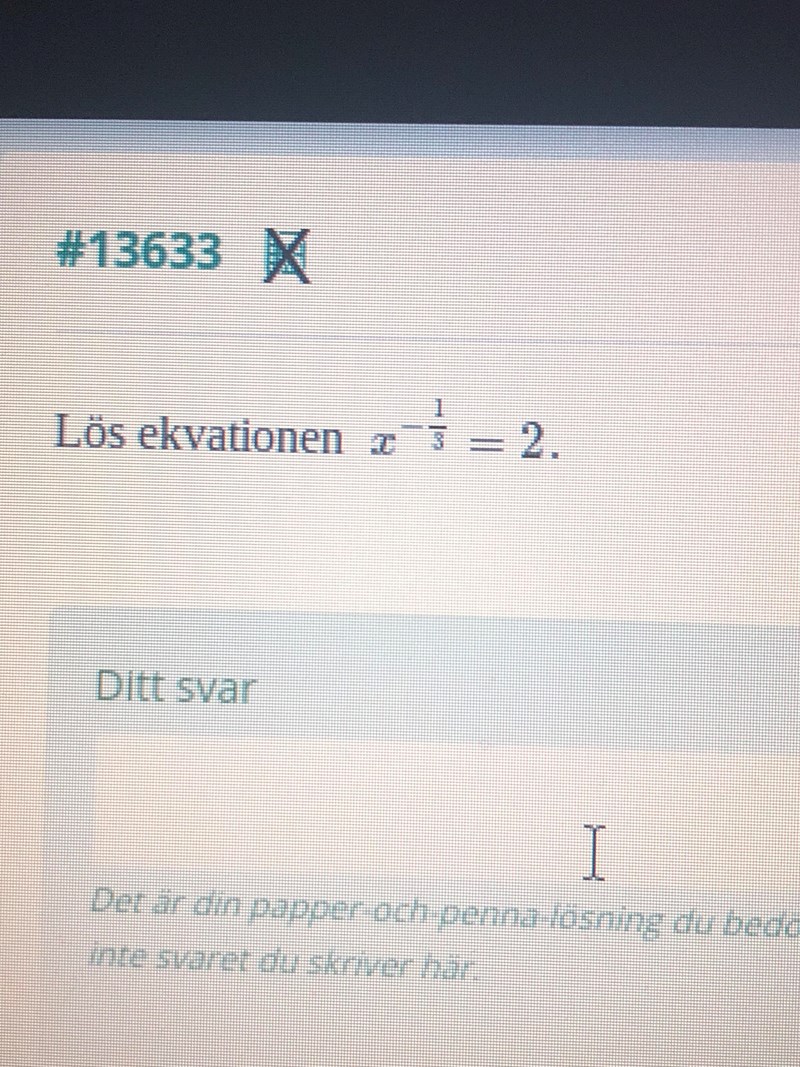 Jag vet hur man löser en ekvation som har en positiv exponent x^(1/3) =2
Jag vet hur man löser en ekvation som har en positiv exponent x^(1/3) =2
Man tar x^(1/3)*3 = 2^1*3
x=2^3=8
Men x^(-1/3)
Är det 3:an som är negativ, är det hela bråket? Hur ska man tänka där? Man ska väl ta -1/3 * (-3)?
Renny19900 skrev:
Jag vet hur man löser en ekvation som har en positiv exponent x^(1/3) =2
Man tar x^(1/3)*3 = 2^1*3
x=2^3=8
Men x^(-1/3)
Är det 3:an som är negativ, är det hela bråket? Hur ska man tänka där? Man ska väl ta -1/3 * (-3)?
Ja. Vad händer om du gör så, dvs höjer upp bägge sidor till -3?
Då blir det 2^(-3)
Men det som egentligen förvirrar mig är självaste exponenten, det står - 1/3
är det ettan som är negativ eller hela bråket? Hur ska man tolka det?
för (-3) * (-1) / 3 = 3/1
Renny19900 skrev:Då blir det 2^(-3)
Men det som egentligen förvirrar mig är självaste exponenten, det står - 1/3
är det ettan som är negativ eller hela bråket? Hur ska man tolka det?
för (-3) * (-1) / 3 = 3/1
Var minustecknet "hamnar" spelar ingen roll eftersom
Fortsätt, du är på rätt väg. Vad får du för resultat?
Om det är 1/(-3) blir talet som jag ska upphöja med (-3)
Om det istället är (-1)/3 så måste man ta (-1)*(-3) dvs upphöja med (-3) vilket ger 1. Du har rätt!
Det blir
2^(-3) = 1/2^3 = 1/8
———————
Bara för att känna mig lite säkrare, skulle du snälla kunna skriva ett exempel som är svårare? Skulle uppskattas :)
Renny19900 skrev:
Om det är 1/(-3) blir talet som jag ska upphöja med (-3)Om det istället är (-1)/3 så måste man ta (-1)*(-3) dvs upphöja med (-3) vilket ger 1. Du har rätt!
Det blir
2^(-3) = 1/2^3 = 1/8
———————
Bara för att känna mig lite säkrare, skulle du snälla kunna skriva ett exempel som är svårare? Skulle uppskattas :)
Bra. Det är rätt.
För att bli säkrare kan du använda en annan lösningsmetod och jämföra resultaten.
Multiplicera båda sidor med :
Förenkla:
Dividera båda sidor med 2:
Upphöjt båda sidor till 3:
Samma resultat.
--------
"Svårare" exempel:
Jag vet inte om jag har löst den rätt :
Renny19900 skrev:Jag vet inte om jag har löst den rätt :
Som med all ekvationslösning: Pröva!
Sätt in resultatet i ursprungsekvationen. Visar den då en likhet så är resultatet rätt, annars inte.
Vad händer om du ersätter med i ursprungsekvationen?
Jag testade att sätta in b^a och Fick
b^(-a)+(a)=b alltså att b=b , min lösning verkar rätt!
Renny19900 skrev:Jag testade att sätta in b^a och Fick
b^(-a)+(a)=b alltså att b=b , min lösning verkar rätt!
Ajdå. Du gör samma fel när du prövar din lösning, alltså verkar den rätt fast den inte är det.
Ta en titt på potenslagarna och se om du verkligen använder dem på rätt sätt.
Om du sätter in istället för i ursprungsekvationen så blir vänsterledet , men det är inte lika med
B^(-a) * B^(a)
man ska ju addera exponenterna?
alltså (-a) + (a) = -a+a =0
Jag ser inte felet
(EDIT)
Nu ser jag felet!
Om x = 2^2
och vi har uttrycket x^2=2
så ska man ta (2^2)^2 = 2
Dvs sätta x inom ett parentes och därefter upphöja till samma tal som x upphöjdes med
———————-
Jag testar lösa uppgiften om :
x^(-a)=b
Jag skriver om x^(-a) = b
som 1/(x^a) =b
Vad är nästa steg?
Renny19900 skrev:B^(-a) * B^(a)
man ska ju addera exponenterna?
alltså (-a) + (a) = -a+a =0Jag ser inte felet
(EDIT)
Nu ser jag felet!
Om x = 2^2
och vi har uttrycket x^2=2
så ska man ta (2^2)^2 = 2
Dvs sätta x inom ett parentes och därefter upphöja till samma tal som x upphöjdes med
———————-
Jag testar lösa uppgiften om :
x^(-a)=b
Jag skriver om x^(-a) = b
som 1/(x^a) =b
Vad är nästa steg?
Jag förstår nog inte riktigt ditt exempel med x och tvåorna.
Problemet var att du upphöjde båda led till istället för att multiplicera båda led med .
Nästa steg i din nya ekvationslösning är samma som tidigare, multiplicera bägge sidor med . Då får du talet 1 i vänsterledet och i högerledet.
Kommer du vidare på det spåret?
Alternativ lösningsmetod
Ekvationen är .
Upphöj nu bägge sidor till .
Då får du
Förenkla vänsterledet med hjälp av potenslag:
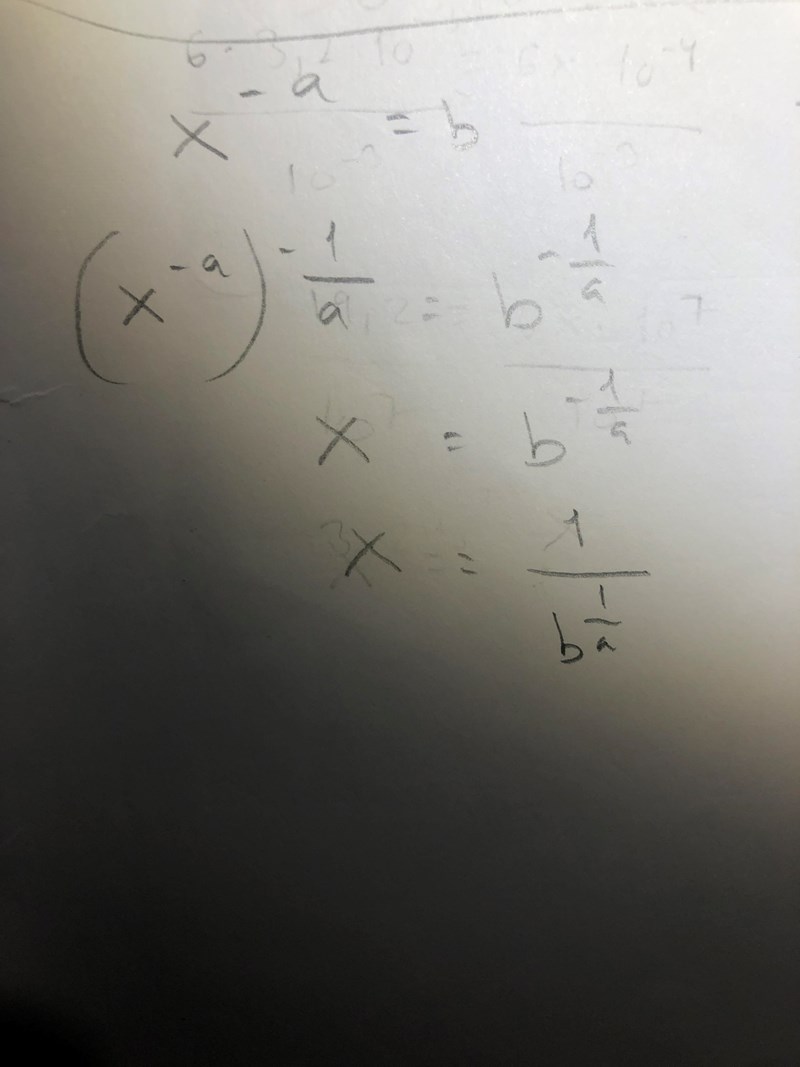 Så här blev lösningen
Så här blev lösningen
Renny19900 skrev:
Så här blev lösningen
OK bra.
Kan du nu kontrollera din lösning?
Det är en jättebra vana.
Nu när jag kontroll räknar blir jag förvirrad. 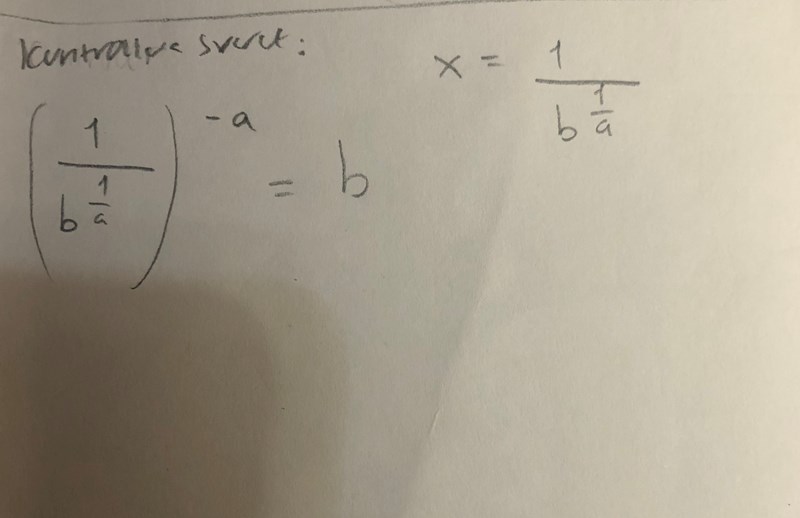 Vad är det jag ska få ut nu när jag kontrollerar min uträkning
Vad är det jag ska få ut nu när jag kontrollerar min uträkning
Renny19900 skrev:Nu när jag kontroll räknar blir jag förvirrad.
Vad är det jag ska få ut nu när jag kontrollerar min uträkning
Ersätt med i vänsterledet, förenkla och kontrollera att det blir samma sak som det som står i högerledet.
Exempel 1:
Jag löser ekvationen 3x + 4 = 13 och kommer fram till att x = 3.
För att kontrollera mitt svar ersätter jag x med 3 i vänsterledet. Det blir då 3*3 + 4. Jag beräknar detta uttryck och får det till 9+4 = 13. Jag jämför nu detta med högerledet och ser att de är samma. Då är jag nöjd och ganska säker på att x = 3 är en lösning till ekvationen.
Exempel 2:
Jag löser ekvationen x/2 - 7 = 5 och kommer fram till att x = 18.
För att kontrollera mitt svar ersätter jag x med 18 i vänsterledet. Det blir då 18/2 - 7. Jag beräknar detta uttryck och får det till 9 - 7 = 2. Jag jämför nu detta med högerledet och ser att de inte alls stämmer överens som de borde. Då är jag ganska säker på att x = 18 inte är en lösning till ekvationen.
Så här blev det.. Ännu krångligare nu. Jag får att 1/ 1^a på vänsterleden och b/b på högerleden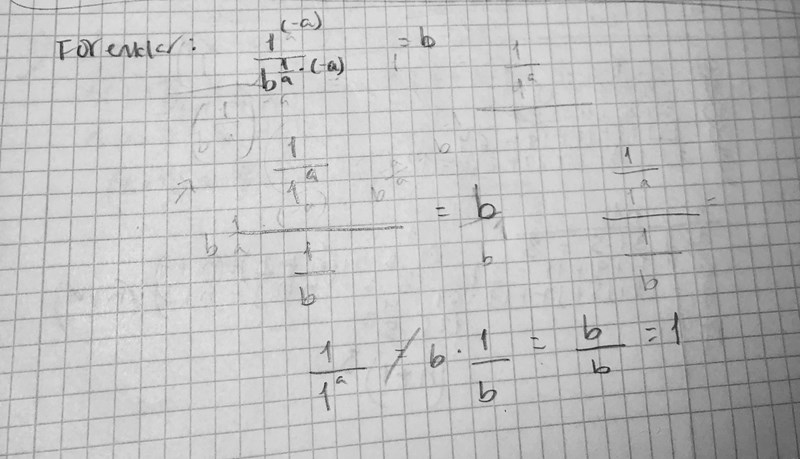
Renny19900 skrev:Så här blev det.. Ännu krångligare nu. Jag får att 1/ 1^a på vänsterleden och b/b på högerleden
Nej, som jag skrev tidigare:
Jobba bara med vänsterledet, sätt in ditt värde på x, förenkla och se vad du får.
Sedan jämför du det med högerledet.
Alltså så här:
Ditt förslag är
Sätt in detta i vänsterledet, dvs i :
Jämför med högerledet. De är lika!
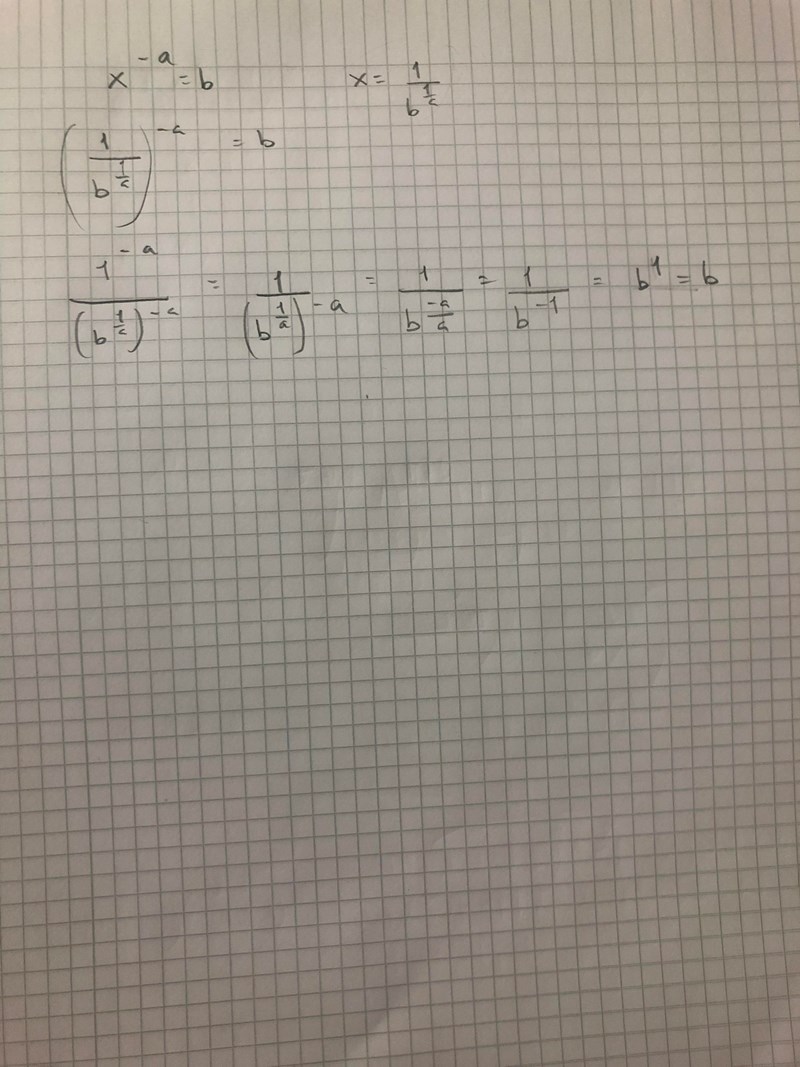 Okej nu förstår jag! Det enda man ska göra är att jämföra VL med HL. Dvs. Sätta in (1/(b^1/2) som också är x därefter upphöja den till -a, om VL är b så kommer lösningen vara rätt. Hade VL inte varit b så skulle lösningen inte stämma... Tusen tack Yngve! Jag uppskattar din tid och tålamod!!!
Okej nu förstår jag! Det enda man ska göra är att jämföra VL med HL. Dvs. Sätta in (1/(b^1/2) som också är x därefter upphöja den till -a, om VL är b så kommer lösningen vara rätt. Hade VL inte varit b så skulle lösningen inte stämma... Tusen tack Yngve! Jag uppskattar din tid och tålamod!!!
——————
Förlåt för att jag är jobbig, men jag älskar utmaningar. Kan du snälla skriva ytterligare en och sista liknanden uppgift? (Förlåt igen!!) Men jag vill vara 110% på att jag fattat.. :)
Renny19900 skrev:[…]
——————
Förlåt för att jag är jobbig, men jag älskar utmaningar. Kan du snälla skriva ytterligare en och sista liknanden uppgift? (Förlåt igen!!) Men jag vill vara 110% på att jag fattat.. :)
Yes!! Jag lyckades lösa den!
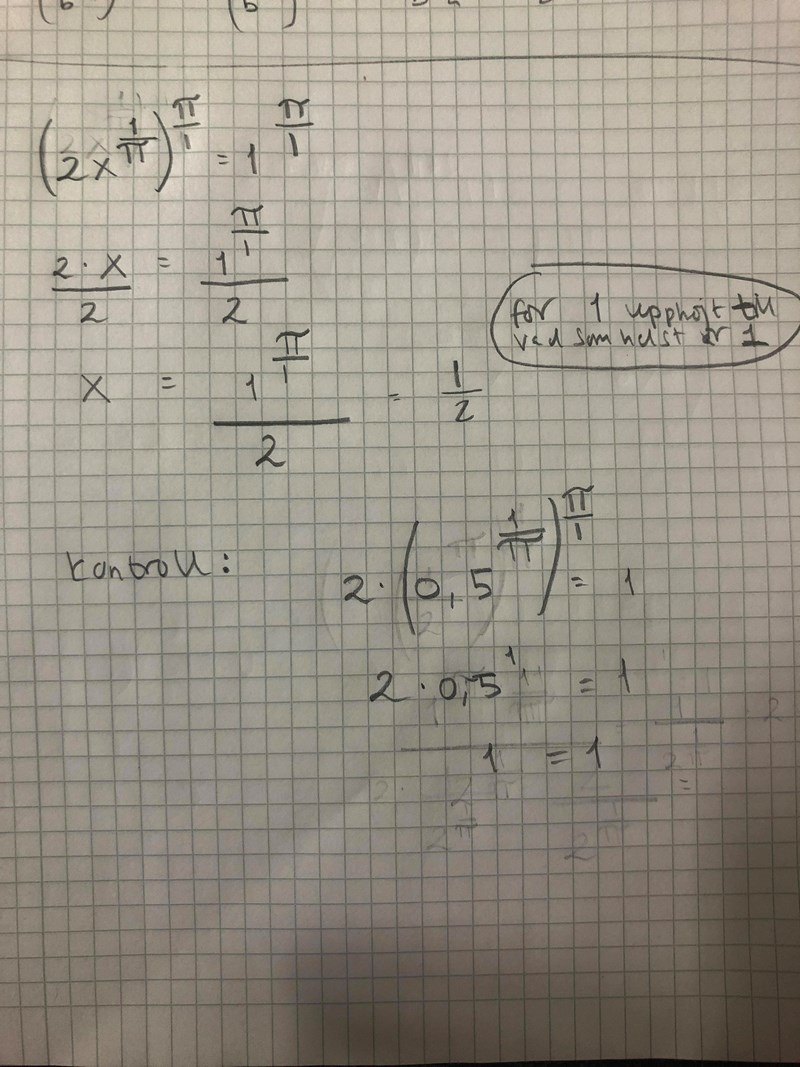
Renny19900 skrev:Yes!! Jag lyckades lösa den!
Nej nu har det blivit lite fel i ekvationslösningen (och lite fel i kontrollen).
Vi börjar med kontrollen:
Du har kommit fram till att
Sedan ska du ersätta med i vänsterledet för att kontrollera ditt resultat.
Eftersom vänsterledet ursprungligen var så borde du då få , men du skriver istället , vilket inte är samma sak.
Gör om kontrollen utan extra räkneoperationer och visa ditt resultat.
(Och återigen, ta inte med högerledet i din kontroll, det förvirrar bara.)
Fundera sedan på var någonstans i ekvationslösningen det kan ha blivit fel.
Felet jag gjorde var att jag inte upphöjde 2 med pi, utan jag upphöjde x^(1/pi) * pi men jag gjorde inte detsamma med 2.
Jag följer potenslagarna :
(a*b)^2 = (a^2)*(b^2)
det jag gjorde var a* b^2 .(detta är bara ett exempel)
——————
Återigen till frågan :
Jag trodde att om man multiplicerar in pi så skulle den tas ut av 1/pi som var med. Men det är fel. 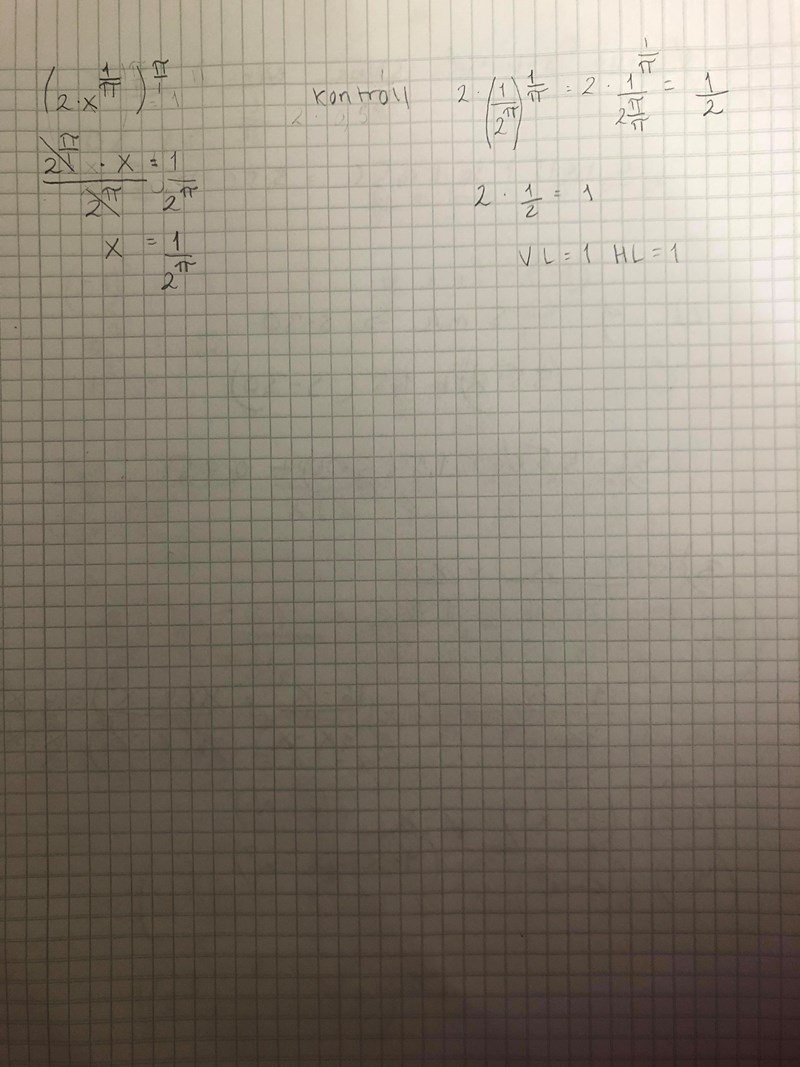
Du har att (ab)c=acbc.
Renny19900 skrev:Felet jag gjorde var att jag inte upphöjde 2 med pi, utan jag upphöjde x^(1/pi) * pi men jag gjorde inte detsamma med 2.
[...]
Du går för snabbt fram.
Börja med att göra om kontrollen på rätt sätt.
Om du har tränat på det så att det fungerar bra så kommer du att ha stor nytta av det framöver.
Om du inte vet hur du ska eller inte kan kontrollera dina svar så kommer du att vid varje uträkning sväva i ovisshet kring om ditt resultat är rätt eller inte. Dessutom kommer du inte att lika lätt kunna upptäcka rena felskrivningar, dvs onödiga fel i uträkningarna.



