POtentialfunktioer
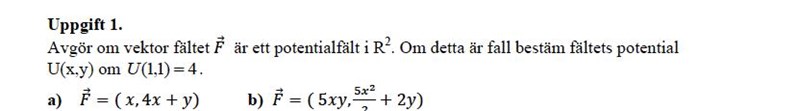
B upppgf..
försöker lösa den på samma sätt som denna:
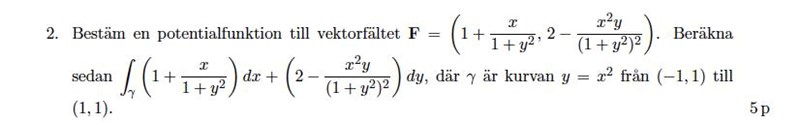

jag gör såhär: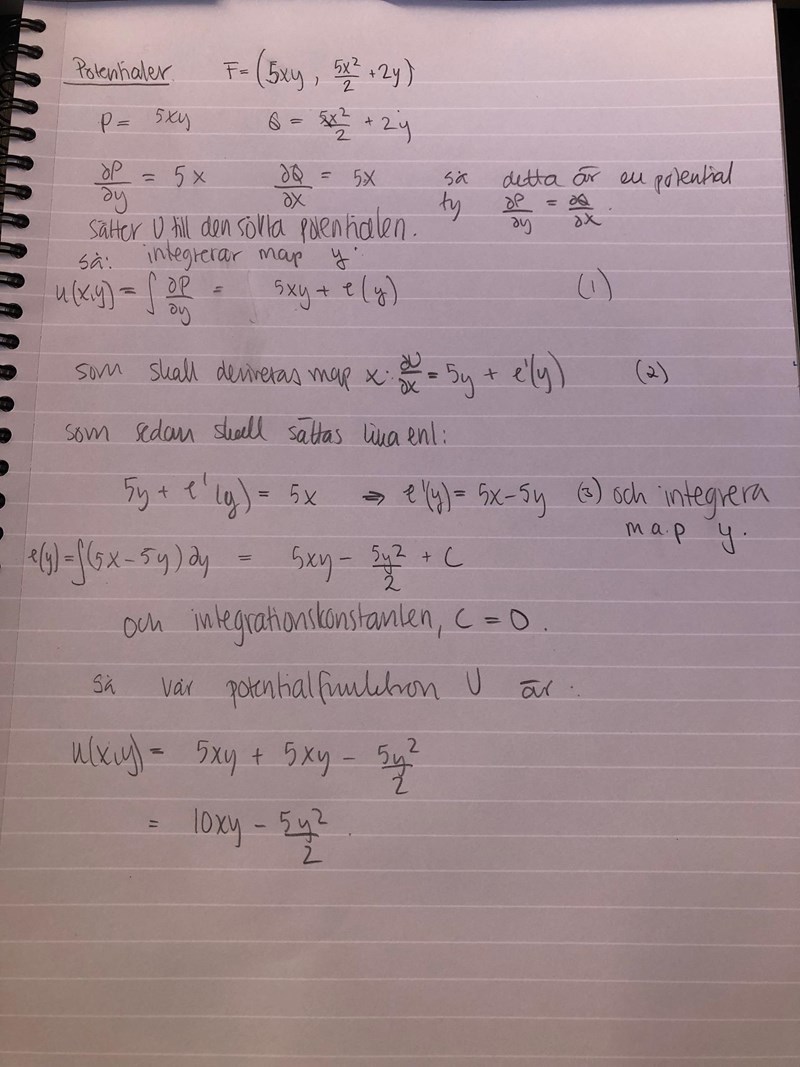
Men vad är fel :S
Integrera P dx och Q dy, inte deras derivator.
Laguna skrev:Integrera P dx och Q dy, inte deras derivator.

MEn svaret är
Hur?
Du glömmer att när du integrerar ekvationen får du även en konstant , d.v.s. .
Denna konstant kan du bestämma med hjälp av villkoret .
AlvinB skrev:Du glömmer att när du integrerar ekvationen får du även en konstant , d.v.s. .
Denna konstant kan du bestämma med hjälp av villkoret .
Men trodde man alltid satte integrationskonstanen till 0?
Om man använder potentialfunktionen för att beräkna en kurvintegral sätter man konstanten till noll för enkelhetens skull (eftersom integrationskonstanterna tar ut varandra i subtraktionen), men nu har vi ju ett villkor som potentialfunktionen skall uppfylla. Då måste vi räkna fram ett värde på konstanten.
Jämför med envariabelfallet. När vi tar fram en primitiv funktion för att beräkna en integral sätter vi konstanten till noll för enkelhetens skull, men om vi har ett villkor, t.ex. att , måste vi räkna fram ett värde på konstanten.
AlvinB skrev:Om man använder potentialfunktionen för att beräkna en kurvintegral sätter man konstanten till noll för enkelhetens skull (eftersom integrationskonstanterna tar ut varandra i subtraktionen), men nu har vi ju ett villkor som potentialfunktionen skall uppfylla. Då måste vi räkna fram ett värde på konstanten.
Jämför med envariabelfallet. När vi tar fram en primitiv funktion för att beräkna en integral sätter vi konstanten till noll för enkelhetens skull, men om vi har ett villkor, t.ex. att , måste vi räkna fram ett värde på konstanten.
Men ändock.. svaret ska ju fortf bli det jag skrev, utan det villkoret...
På tredje raden har du skrivit just
.
Hur kunde det bli
på sista raden?
Man sätter bara integrationskonstanten till 0 om man vill räkna ut en bestämd integral. Nu är uppgiften att finna en potential som uppfyller ett visst villkor, inte att räkna ut en integral och då är det givetvis felaktigt att svara med en potential som inte uppfyller villkoret.
Hej!
- Vektorfältet (och inte vektor fältet, som läraren skriver) är ett potentialfält om rotationen är lika med nollvektorn över hela vektorfältets definitionsmängd.
Beräkna rotationen och undersök om den verkligen är lika med nollvektorn överallt.
- Om verkligen är ett potentialfält så finns det ett skalärfält sådant att dess gradientfält är just det givna vektorfältet det vill säga .
Det betyder att
och
där och .
- Den första ekvationen medför att där är en godtycklig deriverbar funktion.
- Den andra ekvationen medför att vilket betyder att där betecknar en godtycklig konstant.
Om verkligen är ett potentialfält så är dess associerade potentialer funktionerna
och av dessa är det bara funktionen
, där ,
som uppfyller kravet
Aerius skrev:På tredje raden har du skrivit just
.
Hur kunde det bli
på sista raden?
Ja jag vet inte om
dU/dx = xy
dU/dy = 5x^2/2 + 2y
och jag väljer att integrera på dU/dx först, är det det som bir slutgiltiga svaret?
mrlill_ludde skrev:Aerius skrev:På tredje raden har du skrivit just
.
Hur kunde det bli
på sista raden?
Ja jag vet inte om
dU/dx = xy
dU/dy = 5x^2/2 + 2y
och jag väljer att integrera på dU/dx först, är det det som bir slutgiltiga svaret?
Jag förstår inte vad du skriver. Om ordningen: det spelar ingen roll vilket uttryck du integrerar först.
Poängen är ju att när du integrerar derivatan av får du ett uttryck för .
Du får alltså:
När du sedan bestämt att är det bara att sätta in detta i uttrycket du får fick fram när du integrerade -derivatan:




