Primitiv funktion
funktionen f(x)= 1/x2 + 2 och man ska beräkna integralen av den mellan intervallet -1 och 1. En av frågorna är varför integralen inte kan beräknas med primitiv funktion då den blir odefinierad i geogebra, men den går att räkna för hand. Min fråga: varför blir den odefinierad?
tacksam för svar.
pinkcore skrev:funktionen f(x)= 1/x2 + 2 och man ska beräkna integralen av den mellan intervallet -1 och 1. En av frågorna är varför integralen inte kan beräknas med primitiv funktion då den blir odefinierad i geogebra, men den går att räkna för hand. Min fråga: varför blir den odefinierad?
tacksam för svar.
Rita upp funktionen, så kan du nog se det! Om du inte ser det: lägg upp bilden här, så kan vi diskutera vidare från den.
Jag ser att med intervallet -1 och 1 så tar de väl ut varandra och blir 0, men det är väl fortfarande definierat? det blir väl bara 0
Lägg upp din bild här. Det är meningslöst att diskutera vidare utan en bild.
Förresten, är funktionen , som du har skrivit, eller , d v s f(x) = 1/(x2+2)? Jag tolkade det som den första, men jag är inte alldeles säker.
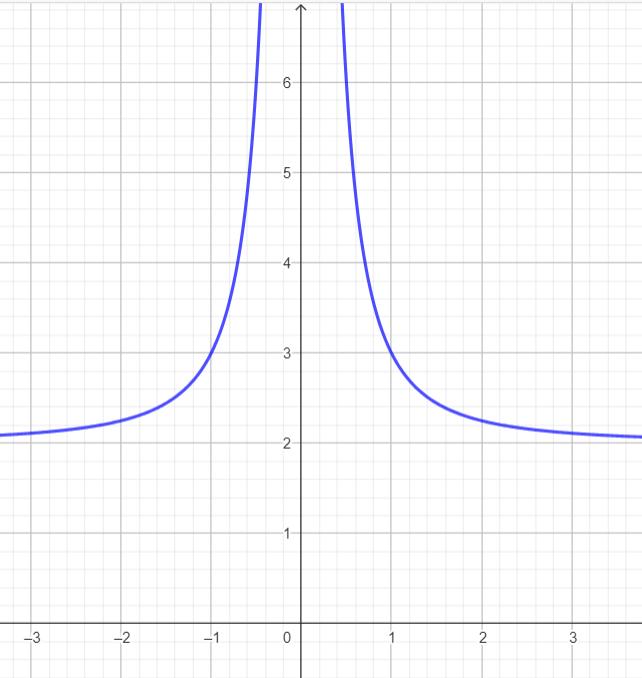den första alltså 1/x^2 + 2
Vad händer när x = 0?
det är väl att ingenting händer när x är noll då grafen aldrig skär y axeln
Ju närmare 0 som x blir, desto större blir värdet på y. Vad tror du händer med arean under kurvan?
Arean blir väl också större eller blir den mindre för att man multiplicerar med något som blir närmare 0?
Hur stor blir arean om man går ända fram till x = 0?
den blir 0
Nej, det blir den inte.
