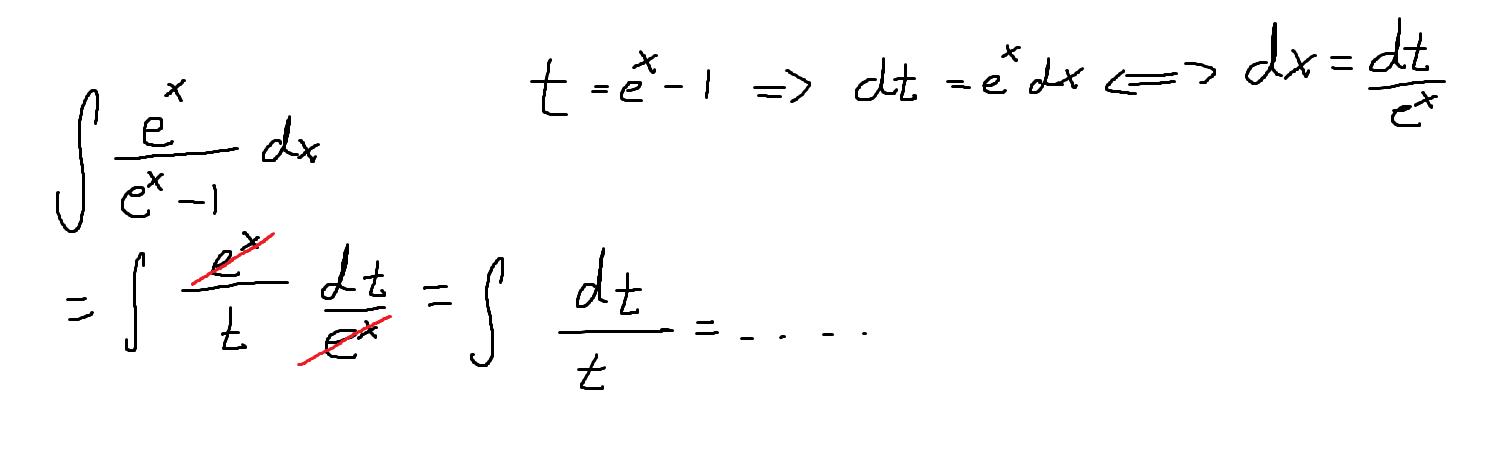Primitiv funktion med e^x
Hej, jag skulle behöva hjälp med att ta fram en primitiv funktion till . Nedan infogar jag en bild på hur jag har gjort. I slutet får jag med men den ska inte vara med :/
Jag har ingen riktig metod, men nämnaren får mig att tänka på ett ln-uttryck. Jag provar att derivera ln[e^x –1]. Och det verkar vara svaret. En konstant behöver tillföras förstås.
Först nu såg jag din bild, den kom senare. dx = dt/ (t–1) så uttrycket du ska integrera blir
(t–1) / [t(t–1)] = 1/t.
Det ger samma svar.
hur får du fram att dx ska bli det? Får något annat...
Du har dx = dt/e^x.
e^x –1 = t så e^x = t+1, ajaj det var ett teckenfel där, sorry!
Jag skulle ha skrivit [(t+1)/(t(t+1)]dt
Men din lösning var snygg!
Nu hänger jag inte alls med. Hur får du fram det? Varför blir det plus 1 i täljare och nämnare?
Jag skriver för hand och postar en bild.
Super, har ytterligare en fråga sen
hoppas bilden syns, haft problem med att de inte syns tidigare
Du har integralen av (e^x+1)/e^x. Men här är det helt onödigt med substitution. Du kan skriva integranden som e^x/e^x + 1/e^x = 1+ e^(–x). Integralen av 1 är x och int av e^(–x) är –e^(–x).
Om du försöker integrera 1/e^x med en lnfunktion så funkar det inte eftersom du får en inre derivata som sabbar. I tidigare exemplet så stod inre derivatan redan i täljaren, mycket tacknämligt.
Tusen tack!