Primitiv funktion till komplicerat rotuttryck
Hej! Jag försöker räkna ut den primitiva funktionen till följande rotuttryck: . Fastnar dock i hur jag ska göra med den "inre derivatan".
Jag tänker att man kan i vanlig ordning kan skriva om funktionen till . Då får vi väl inledningsvis, men hur ska man fortsätta här? Det finns ju en funktion inuti rotuttrycket också, alltså . Ska man bara dela bort det (som motsats till att gångra med den inre derivatan)? Eller ska man dela bort den motsvarande primitiva funktionen (alltså )? Blev väldigt förvirrad av allt detta ...
Pröva att bryta ut ett t ur rotuttrycket.
Ser du något du känner igen då?
Fundera på om du måste hantera de båda fallen t < 0 och t > 0.
Utbrytning ger . Då kan jag använda partiell integration och kan derivera rotuttrycket istället. Var det det du tänkte på? Ska testa det.
(Vad gäller båda fallen har vi i uppgiften faktiskt ett intervall givet, jag tog bara inte med intervallet då jag tänkte att det nog inte är relevant för uppgifen.)
Enligt facit ska det iallafall bli en sådan här enkel primitiv funktion.
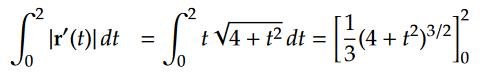
Ja, detta eftersom är inre derivatan till (sånär som på en konstant).
Nej, jag förstår ändå inte riktigt hur jag ska göra ...
Om definitionsmängden till inte innehåller negativa tal så har vi att
Vi ser att derivatan av är vilket gör att vi gissar på följande primitiva funktion till :
Vi deriverar och får då
Nästan rätt, sånär som på en faktor
Vi anpassar och gissar en ny primitiv funktion
Derivera och kontrollera:
Rätt!
"Vi ser att derivatan av 4+t2 är 2t vilket gör att vi gissar på följande primitiva funktion"
Vad är detta för en metod - variabelsubstitution?
Nej, det är kedjeregeln "baklänges".
Men du kan substituera u = 1+t2.



