Problelösningar av derivata - svår uppgift
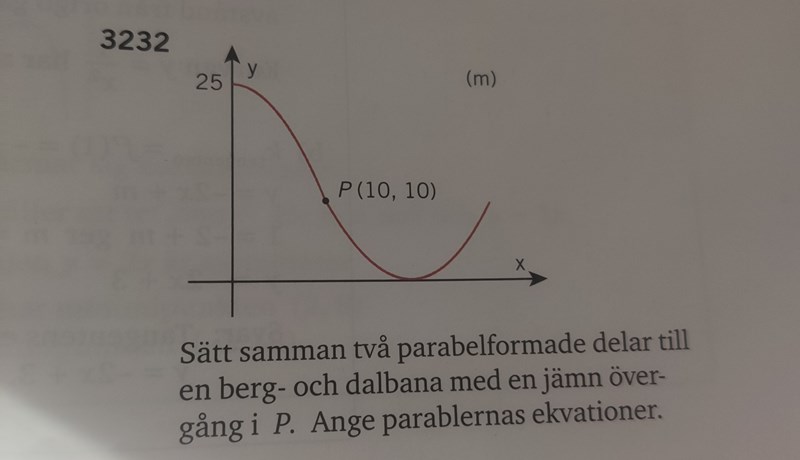
På den vänstra parabeln kan jag räkna ut den rätt enkelt. Jag vet ju att punkten P(10,10) också har en punkt q(-10,10), sedan vet jag också att c-värdet är 25. Detta blir då ett tvåekvationsystem som jag lätt kan lösa.
Den andra parablen är dock lite svårare för mig. Vad ska jag göra? Jag vet att den andra bara nuddar x axeln så den måste väl bara ha ett nollställe. Sedan måste de två parablarna ha samma derivata vid x=10 och också samma y värde
Utnyttja att den högra parabeln har en dubbelrot. Då kan den skrivas på formen y=k(x-a)2 där a är nollstället. Kommer du vidare?
Det mest allmänna sättet att skriva en andragradsfunktion är ax2+bx+c, och du har nämnt tre krav som den ska uppfylla, så du kan få tre ekvationer som tillsammans ger a, b och c.
Uhh så den andra parabeln måste fylla några krav.
1. Den måste ha lutningen -3 (baserat på vad den första parabeln hade för lutning vid punkten x=10)
2. Den måste passera (10;10)
3. k(x-a)2 = -0.15x2 + 25 (först funktionen)
Vet inte hur jag ska göra nu
Ditt tredje villkor är fel - det du har skrivit gäller den vänstra parabeln, inte den högra.
Uhh hur är den sista fel. Båda funktionernas y värde ska vara lika när x=10
Då vet du att
- y=k(x-a)2 (som även kan skrivas y=kx2-2kax+a2)
- y(10)=10
- y'(10)=-3
Kommer du vidare?
Jag vet hur man kan implementera de sista två villkoren men inte den första tyvärr
Derivera funktionen y=k(x-a)2. Vad blir derivatan? Sätt derivatan i punkten x = 10 lika med -3. Du vet också att funktionsvärdet i punkten x = 10 är 10. Detta ger dig ett ekvationssystem med två ekvationer och två obekanta. Lös det som du lärde dig i Ma2.




