Problem komplexa talplanet
Jag har fått detta problemet:
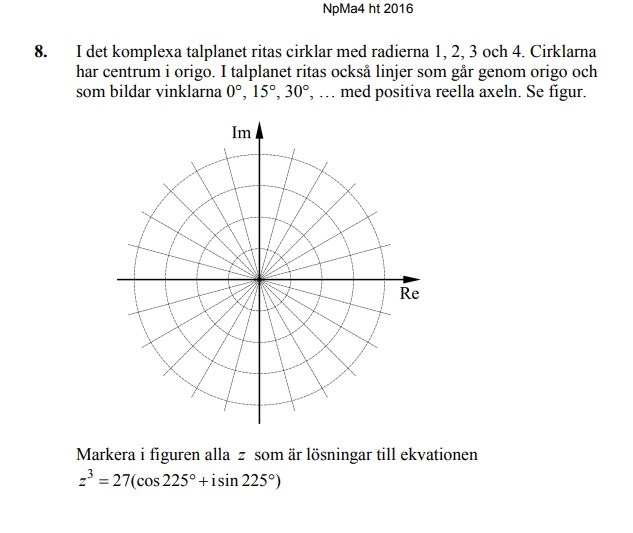
Jag skriver om det med hjälp av de moivres formel så att jag får att z^3= 3^3(cos3v +isin3v)
En lösning är alltså då att 3v=225 och v är 75. Och alla lösningar måste ligga på cirkeln med radien 3. Men hur kan jag hitta de andra lösningarna?
För om jag tar att 225= 180-3v får jag bara lösningar som stämmer överens med sinus. Jag förstår att det gäller att sin3v visar samma värde som cos3v, vilket inträffar vid vinkeln 45*. Varför är då inte v=15 en lösning? Den fanns inte med i facit. Och hur kan jag hitta de andra lösningarna?
Man får inte använda digitala hjälpmedel på denna uppgiften.
3v ska vara 225 grader
...Eller 225 grader plus ett varv
...Eller kanske plus två varv Eller minus tjugosju varv...
225 + N*360
men då blir ju alla mina markeringar bara samma punkt?
Ja, markeringar av z^3 blir samma punkt.
Markeringar av 3v blir samma vinkel.
Markeringar av v blir inte det.
Som jag (nästan) skrev tidigare :
3v = 225 + N*360
men i facit finns det fler punkter utritade. 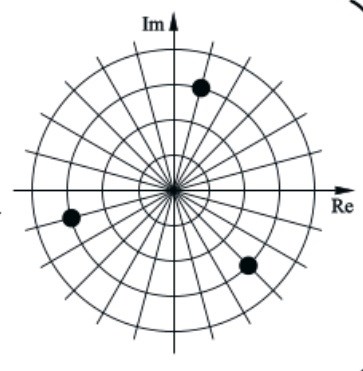
Det antyds att v=75 + n*120. D v s även 195 och 315 som är de två andra prickarna för n=1 och 2.
Vilka blir lösningarna för Z = ? (2 st)
Hur blir ekvationen för en "Mercedes-stjärna"?
Det är egentligen "enklare" att använda =(cos+i sin) . Då ser man tydligare hur man snurrar
runt i enhetscirkeln.
Lovis0817 skrev:men i facit finns det fler punkter utritade.
Just det. Bilden visar v.
V kan vara 75 grader, ser man. Vad blir då 3v?
V kan vara 195 grader, ser man. Vad blir då 3v?
V kan vara 315 grader, ser man. Vad blir då 3v?

