Problem lösning 5
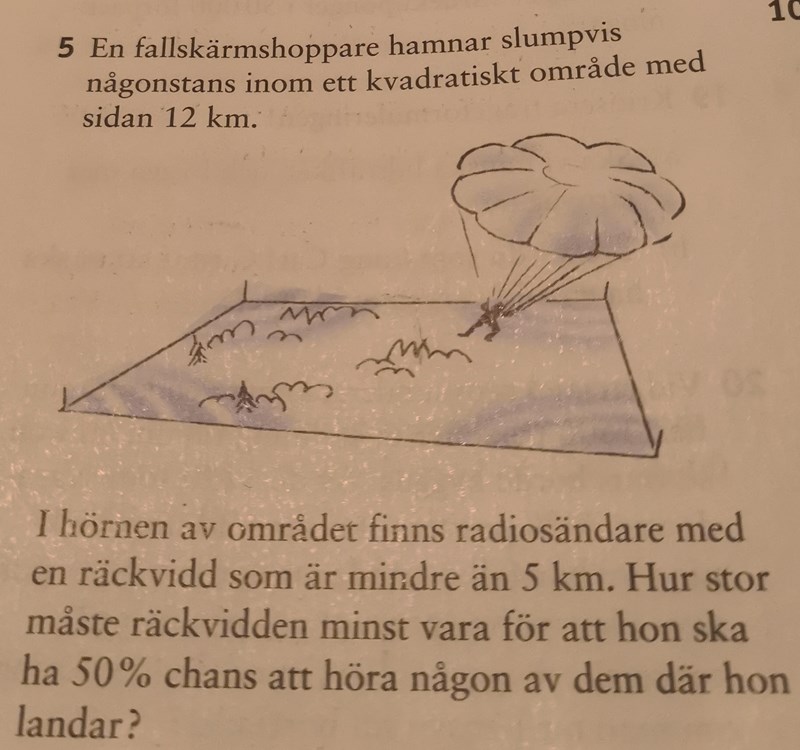
Vet inte hur jag ska gå till väga.
Kvadratens Area = 144km2
räckvidd radiosändare <5km
Rita en figur av en kvadrat uppifrån.
Låt kvadratens sidlängd vara 12 längdenheter.
Rita fyra cirklar med medelpunkt i hörnen och ned en radie på 5 längdenheter.
Ser du då hur du kan gå vidare?
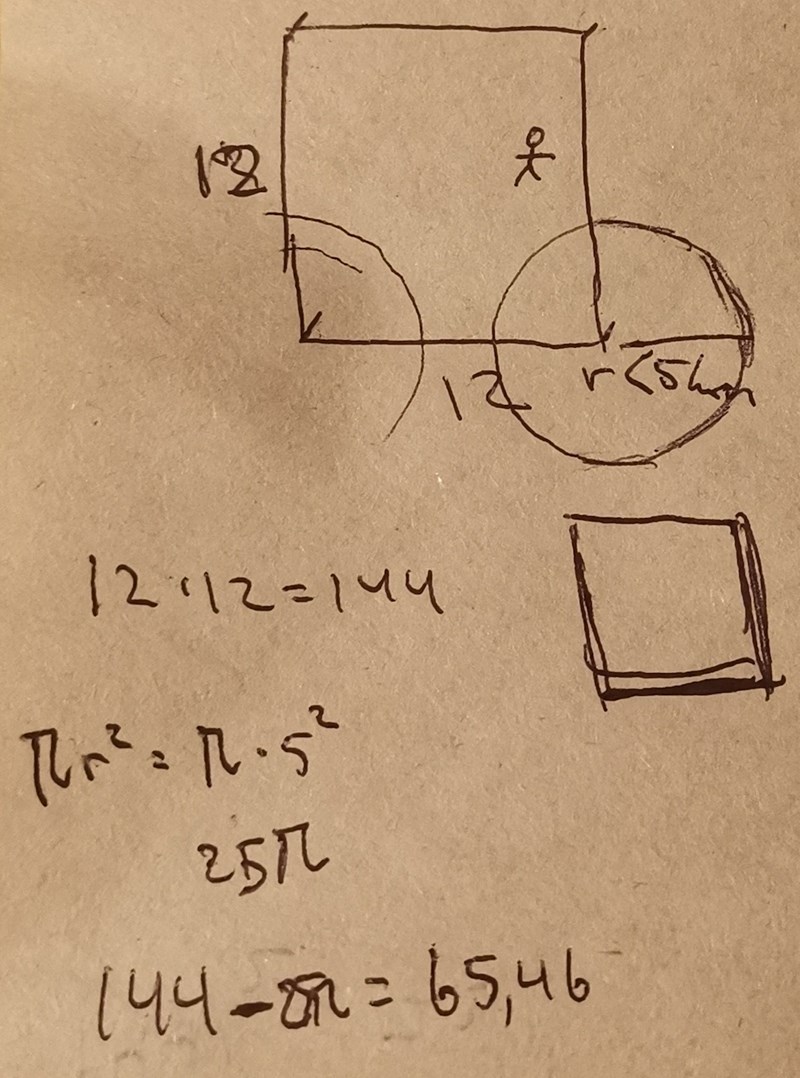
Jag har redan gjort detta.
Men jag förstår inte riktigt hur jag går vidare
Bra.
Är du med på att sannolikheten för att hopparen hamnar inom räckvidden för någon av radiosändarna är lika med förhållandet mellan kvartscirklarnas sammanlagda area och kvadratens area?
Jo det är jag
OK bra, och kvartscirklarnas sammanlagda area är ju, som du mycket riktigt konstaterat, lika med , där är den räckvidd vi söker.
Förhållandet mellan denna sammanlagda area och kvadratens area är alltså lika med .
Du vill att denna kvot ska vara minst 0,5.
Förstår du varför?
Jag tror att jag förstår.
Vi vill att kvoten ska bli 50%. Eftersom att hopparen ska ha 50% chans att höra någon av radiosändarna...
(Pi*r2) /144 = radiosändarnas täckning per kvadratiskt område.
Ja det stämmer. Olikheten blir
Varför kallar vi det en olikhet?
Vi vill ju att VL skall bli större än eller lika med HL. Det är helt OK om sannolikheten är större än 50 % att sändaren skall höras (men r får inte vara mer än 5 km, det står i uppgiften).
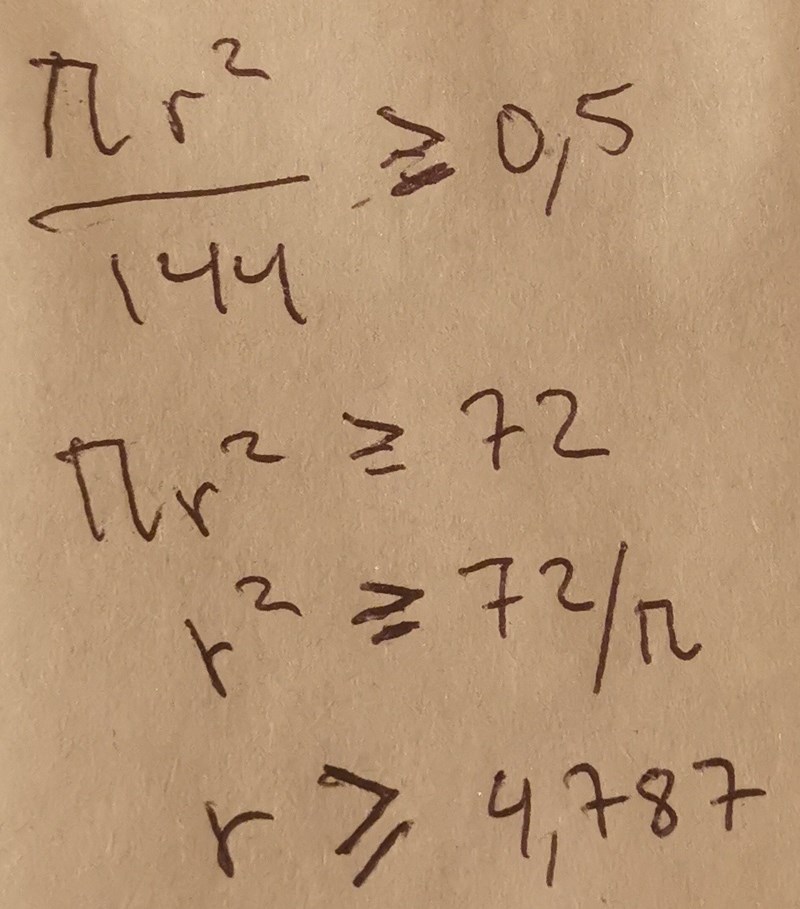
Så räckvidden är
4,8<= r <5
Ja, svaret är att räckvidden måste vara minst 4,8 km.





