Problem med att lösa ut DS och ds

Hej jag har följande uppgift. Men är lite förvirrad över lösningen i facit då dom skall räkna ut dS. Jag trodde att man skulle tänka dS som längden av kurvan och höjden på z som i den här bilden: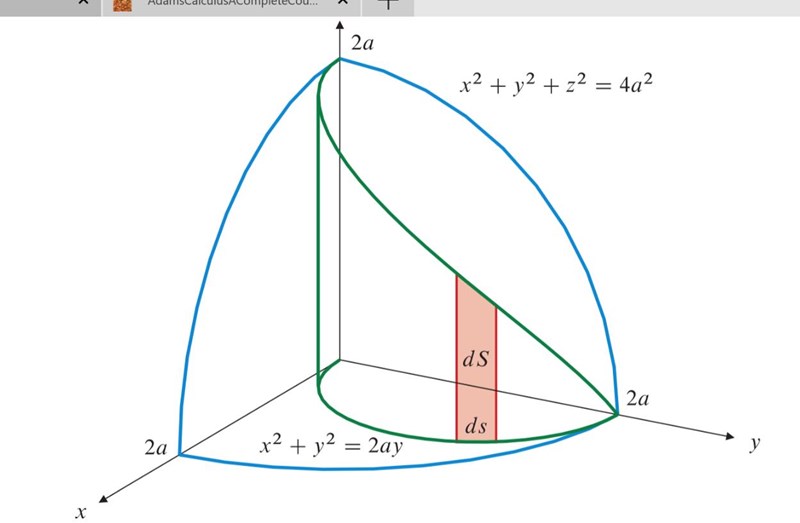

Ds är väll i kurvan

$x^{2} + y^{2} = 2 a y$

och derivera den med avseende på x ? Vilket blir $x^{2} + y^{2} = 2 a y - - > x^{2} + (y - a)^{2} - a^{2} = 0 - - > (y - a)^{2} = a^{2} - x^{2} - - > y = \sqrt{a^{2} - x^{2}} + a d y / d x = \frac{- 2 x}{\sqrt{a^{2} - x^{2}}}$

DS måste vara höjden. Men den kan jag inte riktigt förstå.

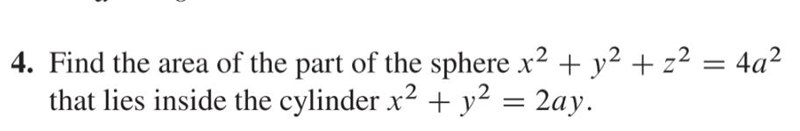
Annvänder man det att DS = $\sqrt{1 + (f' x)^{2} + (f' y)^{2}}$

Men i det här fallet då z = $\sqrt{4 a^{2} - x^{2} - y^{2}}$

så $\frac{d z}{d x} = \frac{- 2 x}{\sqrt{4 a^{2} - x^{2} - y^{2}}}$

och liknande med dz/dy och då blir $D S = \sqrt{1 + \frac{4 (x^{2} + y^{2)}}{z^{2}}}$

och det är ju likt facit men inte exakt. Vad gör jag för fel?

Det verkar som om du tror att du skall räkna ut någon volym, eftersom du tror att dS skulle vara höjden, men höjden är helt ointressant i det här fallet. Det som gäller är att ds är en infinitesimalt liten del av cirkelskivan i xy-planet och att dS är motsavarande lite större del på sfärens yta.

Jag såg mitt fel. dz/dx = -x/z och inte -2x/z

I dS betyder S surface, alltså yta. Varför kurvlängd kallas s vet jag inte, men det är tradition.

Att ha både s och S i samma uträkning känns lite osäkert, om man skriver för hand.

Svara

Visa senaste svar