Problemlösning
Det enda jag hittills har förstått är :
omloppstiden för alla planeter upphöjt till 3 delat med avståndet till solen upphöjt till 2 ger en lika lång sträcka... Jag vet inte hur jag ska lösa den uppgiften.
Tacksam för hjälp!
Renny19900 skrev:Det enda jag hittills har förstått är :
omloppstiden för alla planeter upphöjt till 3 delat med avståndet till solen upphöjt till 2 ger en lika lång sträcka... Jag vet inte hur jag ska lösa den uppgiften.
Tacksam för hjälp!
Kalla jordens omloppstid för och dess avstånd från solen för .
Kalla Saturnus omloppstid för och dess avstånd från solen för .
Sätt in dessa beteckningar i Keplers tredje lag så får du ett samband mellan avstånden.
Solen-jorden :
((Tj)^3)/(1,496*10^8) =konstant
Vad är konstant? Vad är det man räknar ut?
Saturnus :
(29,5^2)/r
Är det så man ska göra?
Renny19900 skrev:Solen-jorden :
((Tj)^3)/(1,496*10^8) =konstant
Vad är konstant? Vad är det man räknar ut?
Saturnus :
(29,5^2)/r
Är det så man ska göra?
"Konstant" är ett konstant tal som är detsamma för både jorden och Saturnus.
Det betyder att
Multiplicera nu med , dividera med och förenkla.
Sedan kan du dra roten ur bägge sidor så får du den kvot som efterfrågas.
Varför skriver man uttryckt så? Vad är det man räknar?
Varför ska man multiplicera r3s och sedan dividera? Är det så man förenklar?
Tack för hjälpen! :)
Renny19900 skrev:Varför skriver man uttryckt så? Vad är det man räknar?
Varför ska man multiplicera r3s och sedan dividera? Är det så man förenklar?
Tack för hjälpen! :)
Uttrycket beskriver Keplers tredje lag som står angiven i uppgiften. Du kan läsa mer om den här.
Förlåt jag skrev fel förut. Det som efterfrågas i uppgiften är kvoten .

Den får du om du förenklar som jag skrev och sedan drar tredjeroten ur bägge led.
Är du med på att Keplers tredje lag leder till sambandet ?
Är du med på att detta samband även kan skrivas ?
Yngve skrev:Renny19900 skrev:Varför skriver man uttryckt så? Vad är det man räknar?
Varför ska man multiplicera r3s och sedan dividera? Är det så man förenklar?
Tack för hjälpen! :)
Uttrycket beskriver Keplers tredje lag som står angiven i uppgiften. Du kan läsa mer om den här.
Förlåt jag skrev fel förut. Det som efterfrågas i uppgiften är kvoten .
Den får du om du förenklar som jag skrev och sedan drar tredjeroten ur bägge led.
Är du med på att Keplers tredje lag leder till sambandet ?
Är du med på att detta samband även kan skrivas ?
Nej, faktiskt inte. Jag förstår inte vad sambandet visar
Renny19900 skrev:
Nej, faktiskt inte. Jag förstår inte vad sambandet visar
Har du läst om planeters rörelse och Keplers lagar i fysikboken?
Har du läst artikeln som jag länkade till?
T är omloppstiden. r är avståndet i km....
konstanten ger oss den totala medelavståndet Till solen som är samma oavsett vilken planet
Renny19900 skrev:T är omloppstiden. r är avståndet i km....
konstanten ger oss den totala medelavståndet Till solen som är samma oavsett vilken planet
T är omloppstiden i år.
r är avståndet i km.
Men konstanten är inte medelavståndet till solen.
Det spelar i den här uppgiften ingen roll vad konstanten har för värde, det viktiga är att den har samma värde för både jorden och Saturnus.
Om vi kallar konstanten för då gäller alltså
Om vi kombinerar dessa två samband får vi den ekvation jag beskrev tidigare.
Är du med på det?
Förresten, kommer den här uppgiften från din fysikbok eller från din mattebok?
Den uppgiften kommer från min mattebok, origo 1c.
Men så har jag löst hittills 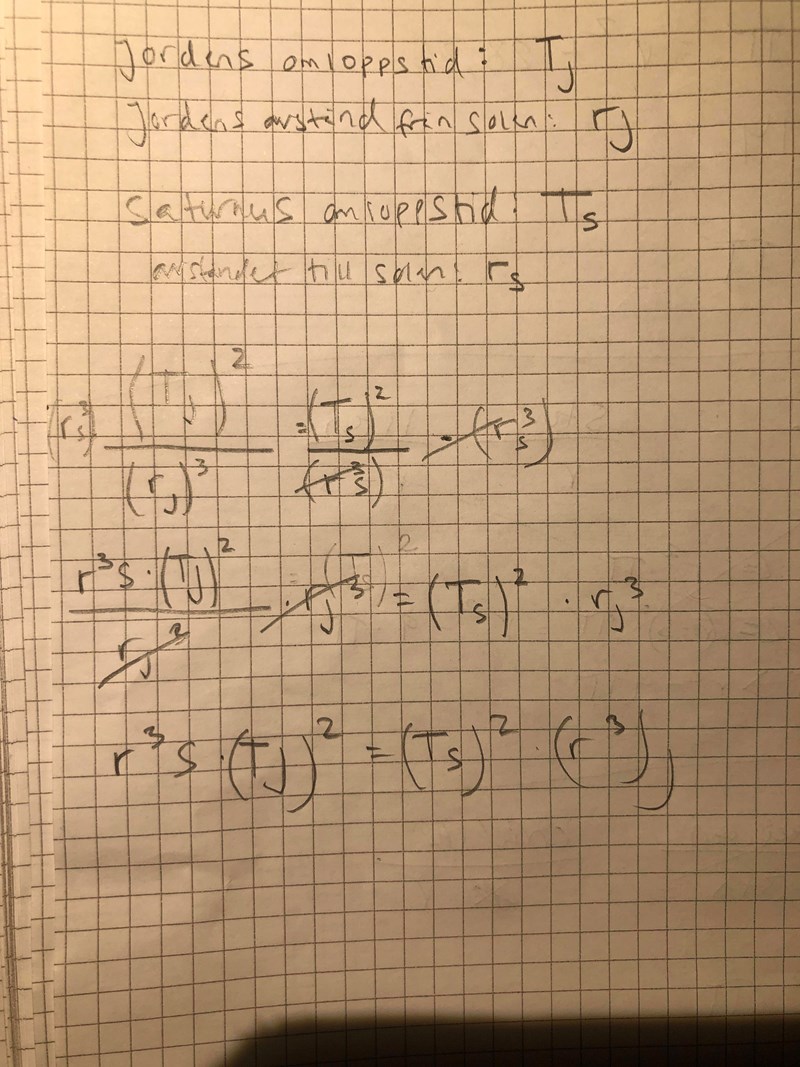
Dina uträkningar är korrekta (men du har skrivit och istället för och ).
Jag föreslog en annan omskrivning så att du skulle få på den ena sidan.
På den andra sidan skulle det då stå svaret på frågan.
Det som efterfrågades var ju nämligen hur många gånger längre det är från solen till Saturnus jämfört med från solen till jorden.
Och detta förhållande är samma sak som.den kvoten jag skrev.
Du kan fortsätta där du har slutat.
Börja med att få ena sidan till .
Dra sedan tredjeroten ur bägge sidor.
Sätt sedan in värden för och så får du svaret.


