Problemlösning - integraler

Har suttit med följande uppgift: "I ett rätvinkligt koordinatsystem ritas en cirkel med radien 1 längdenhet och medelpunkten (0,1). Kurvan y= $\sqrt{x}$ delar cirkeln i två områden. Beräkna arean av det mindre området. För full poäng krävs exakt svar och algebraisk lösning."

Hittills har jag kommit fram till att y= $\sqrt{x}$ och cirkeln skär varandra i (0,0) samt (1,1). Jag har också räknat ut att arean för y= $\sqrt{x}$ i intervallet $0 \leq x \leq 1$ och är $\frac{2}{3}$ a.e. Dessutom vet jag nu att cirkelns area är $π$ a.e. Problemet är att jag inte vet vad jag ska göra med den information jag nu har och hur jag ska ta mig vidare för att beräkna det lilla områdets area. Tacksam för hjälp1 :)

Hur stor är arean mellan cirkelbågen och x-axeln mellan x=0 och x=1?

Laguna skrev:
Hur stor är arean mellan cirkelbågen och x-axeln mellan x=0 och x=1?

Det är det jag inte vet hur jag ska räkna ut. Jag vet att cirkelbågen mellan dessa punkter är $\frac{2 π}{4} = \frac{π}{2}$ men hur ska jag använda denna information för att kunna räkna ut arean mellan cirkelbågen och x-axeln

Anita00 skrev:
Laguna skrev:
Hur stor är arean mellan cirkelbågen och x-axeln mellan x=0 och x=1?
Det är det jag inte vet hur jag ska räkna ut. Jag vet att cirkelbågen mellan dessa punkter är $\frac{2 π}{4} = \frac{π}{2}$ men hur ska jag använda denna information för att kunna räkna ut arean mellan cirkelbågen och x-axeln

Hur stor är cirkelarean nedanför y=1 och till höger om x=0?

Standardfråga 1a: Har du ritat?

Fick ut arean mellan cirkelbågen och x-axeln genom att subtrahera arean av en kvadrat (med ett av hörnen på (0,0) och det andra på (1,1)) med en fjärdedel av cirkelns area. Detta blev: 1- $\frac{π}{4}$ . Därefter subtraherade jag $\frac{2}{3}$ (vilket är arean för y= $\sqrt{x}$ i intervallet x=0 till x=1) med arean mellan cirkelbågen och x-axeln och fick då ut att den eftersökta arean för det lilla området är $\frac{π}{4} - \frac{1}{3}$ a.e, vilket även är svaret i facit! Tack för hjälpen!

EDIT - nu är jag ute och cyklar, se nedan

Nej det du har räknat ut är något helt annat än det som efterfrågas.

Svaret bör vara $\frac{\pi }{4}-\frac{2}{3}$ .

Arean av kvartscirkeln är $\frac{\pi }{4}$ .

Arean under $y=\sqrt{x}$ är $\frac{2}{3}$ .

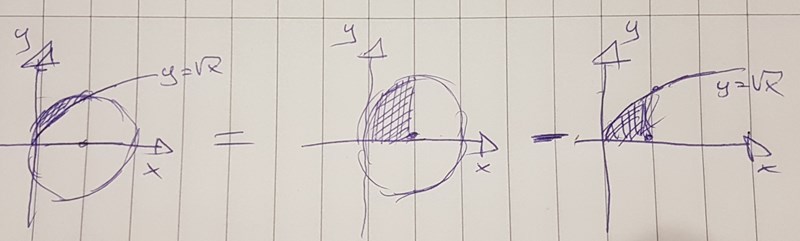
Men cirkelns centrum är (0,1).

Laguna skrev:
Men cirkelns centrum är (0,1).

Haha, ja så är det ju. My bad.

Tänk om jag kunde lägga fokus på att läsa uppgiften ordentligt istället för på att rita en figur 😂

Svara

Visa senaste svar