Problemlösning integraler

myers23232 skrev:

I en tom tank rinner det in vatten med hastigheten (20 – 0,5x) liter/minut, där x är tiden i minuter och 0 ≤ x ≤ 40.

Hur mycket vatten är det i tanken efter

 

a) 10 minuter

Hur vet man vilken nedre och övre integral man ska ta, ska det vara b=40 och a=10 eller a=10 och b=0 ?

Som vanligt, börja med att rita en bild, så klarnar det nog. Om det inte gör det: Lägg in din bild här, så kan vi resonera vidare från den.

Okej jag testar rita bilden

myers23232 skrev:

Okej jag testar rita bilden

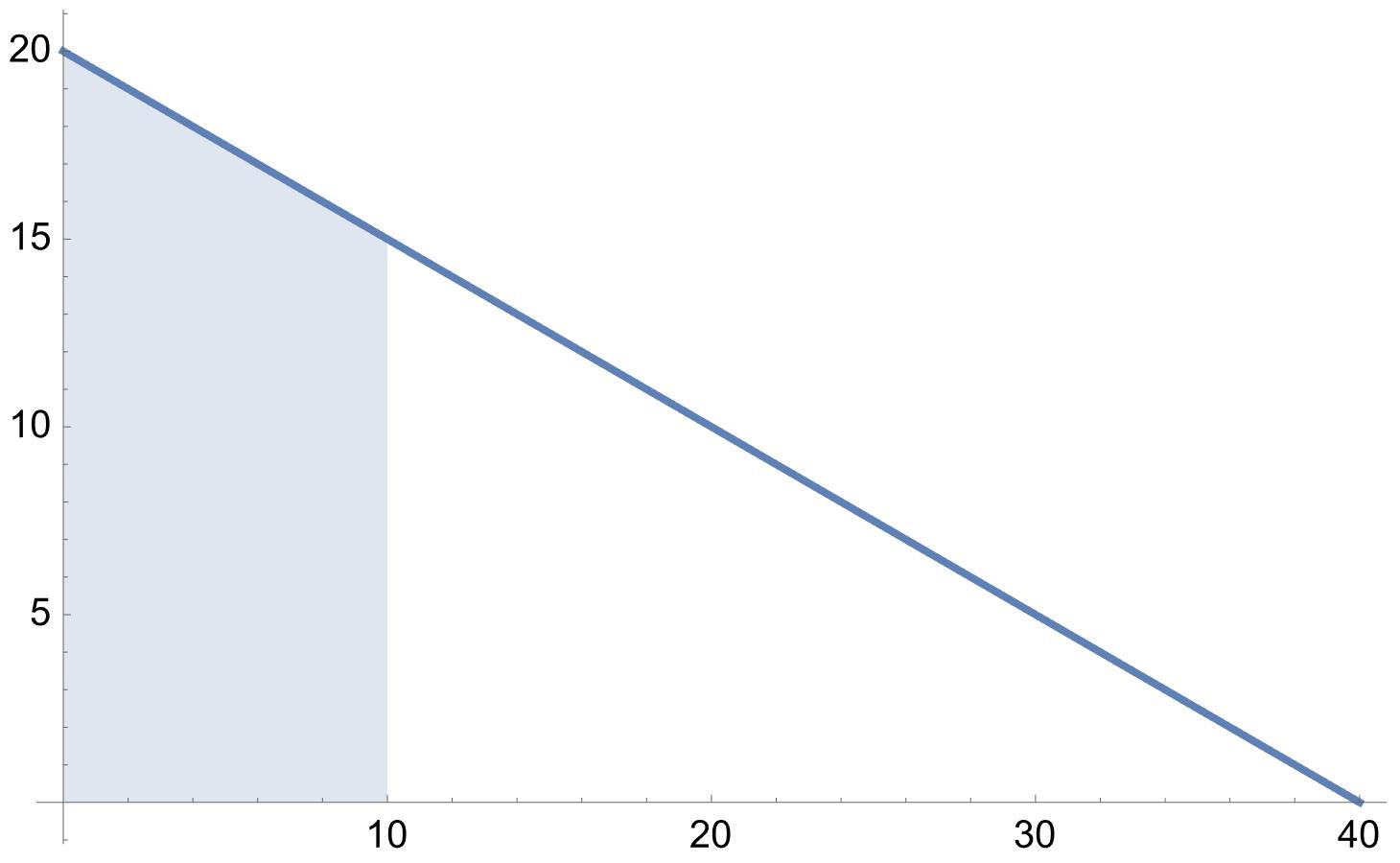
Ja precis tack för en fin bild,  betyder detta att värderna man ska använda är 10 och 40? eller 0 och 10?

myers23232 skrev:

Ja precis tack för en fin bild,  betyder detta att värderna man ska använda är 10 och 40? eller 0 och 10?

"Efter 10 minuter" är lite vagt. Efter vad? Men jag gissar på det är "från starten", dv.s intervallet är [0,10], som det är färgat i bilden.

Notera att det är en rät linje och integralen kan du lätt räkna ut med vanlig geometri, utan att ta primitiv funktion m.m. Alternativt delar du upp det i en triangel och en rektangel.

Ja det står hur mycket vatten är det i tanken när det gått 10 min, ja du har nog rätt så man tänker på starten då är värderna från 0 till 10.