Problemlösning komplexa tal

Antag att det komplexa talet z är sådant att ∣z−c∣=c, där z ≠ 0 och c är ett reellt tal större än noll. Visa Re(1/z)=1/2c

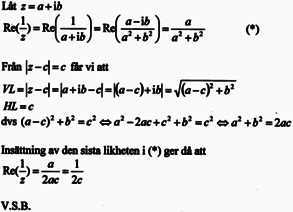
Jag kom fram till där det står "dvs ...=c^2" i facit, sen förstår jag inte varför dem fortsätter så?

Menar du den gulmarkerade delen?

I så fall är förklaringen att de kvadrerar ekvationen $\sqrt{(a-c)^2+b^2}=c$ , vilket ger första ekvationen på den gulmarkerade raden. Sedan använder de första kvadreringsregeln på första termen och förenklar till $a^2+b^2=2ac$

Yngve skrev:
Menar du den gulmarkerade delen?

I så fall är förklaringen att de kvadrerar ekvationen $\sqrt{(a-c)^2+b^2}=c$ , vilket ger första ekvationen på den gulmarkerade raden. Sedan använder de första kvadreringsregeln på första termen och förenklar till $a^2+b^2=2ac$

Den delen förstår jag men hur kopplar dem det till det sista. hur blir a=1??

Vi ser att a är en faktor i både täljaren och nämnaren. Då tar ju a:et i täljaren och a:et i nämnaren ut varandra.

bolibompa skrev:
Den delen förstår jag men hur kopplar dem det till det sista. hur blir a=1??

a blir inte lika med 1.

I sista steget förkortar de med a, vilket är OK om det inte finns någon möjlighet att a = 0.

Den möjligheten bör undersökas innan förkortning sker.

z=c+ce^ia

Invertera och gör reellt genom att förlänga med konjugatet

$\frac{1}{z} = \frac{1 + e^{- i a}}{C (1 + e^{i a}) (1 + e^{- i a})} = \frac{1 + \cos a - i \sin a}{C (1 + e^{i a} + e^{- i a} + 1)}$

(Men cos a = $(e^{i a} + e^{- i a}) / 2$ så )

= $\frac{1 + \cos a - i \sin a}{2 C (1 + \cos a)}$

Där realdelen är 1/2C

hansa skrev:
z=c+ce^ia

Invertera och gör reellt genom att förlänga med konjugatet

$\frac{1}{z} = \frac{1 + e^{- i a}}{C (1 + e^{i a}) (1 + e^{- i a})} = \frac{1 + \cos a - i \sin a}{C (1 + e^{i a} + e^{- i a} + 1)}$

(Men cos a = $(e^{i a} + e^{- i a}) / 2$ så )

= $\frac{1 + \cos a - i \sin a}{2 C (1 + \cos a)}$

Där realdelen är 1/2C

Jag förstår nu tack!

Svara

Visa senaste svar