Problemlösning med ekvationer
Hej, behöver hjälp med en fråga.
Alex vill skaffa körkort och han har två körskolor att välja mellan. Körskola A tar 13500 för paketpris, däribland ingår risk 1an, risk 2an, övningar och även 15 körlektioner. Om man behöver mer än 15 körlektioner kostar det 500 kr per körlektion. Körskola B tar 650 kr per körlektion och deras paketpris är 4500 kr.
a) Vid vilket pris blir de två olika körskolarna samma?
b) Vilken körskola blir billigare?
Först tänkte jag såhär:
A= 13500 + 500x = y, men måste jag inte ta reda på den fasta och rörliga kostnaden i paketpriset?
Man får väl anta att "paketen" exklusive körlektioner har samma innehåll.
Låt x vara antalet körlektioner han behöver.
Vad skulle körkortet kosta hos A som funktion av x ?
Vad skulle körkortet kosta hos B som funktion av x ?
Rita gärna graferna i samma koordinatsystem
Alltså vet inte hur jag ska skriva upp ekvationen eller lösa ut vad körlektionerna kostar ur 13 500 kr.
Var frågorna formulerade just så?
Det borde frågas efter vid vilket antal körlektioner som den sammanlagda kostnaden blir lika för de båda körskolorna.
Och vilken skola som är billigare under respektive över det antalet.
Beroende på om antalet lektioner vid lika totalkostnad (x) är större eller mindre än 15 blir det olika ekvationer.
Ditt uttryck 13500 + 500x för A stämmer inte.
För x<=15 är kostnaden 13500 kr (15 lektioner ingår ju), för x>15 är den 13500 + 500(x-15) kr.
Följ Arktos råd och rita graferna.
Då får du en bättre förståelse av prismodellerna och ser du vilken ekvation du ska ställa upp.
Börja med körskola B.
Efter vid vilket antal körlektioner som den sammanlagda kostnaden blir lika
Ska jag då utgå ifrån körskola A formeln = 13500 kr eller 13500 + 500(x-15)?
B blir 650x+4500?
4500 + 650x för B stämmer. De har bara en prismodell.
För A vet vi inte än. Ritar du graferna kan du se hur det förhåller sig och sedan ställa upp rätt ekvation.
Du kan också börja med ekvationen 4500 + 650x = 13500.
Blir x<=15 var det rätt.
Fast graferna är ändå bra för att se att det inte finns fler skiften i vilken skola som är billigast beroende på antal lektioner.
Varför blir det 4500 + 650x = 13500 ?
Vänsterledet är vad du ställde upp för B.
A har 13500 kr som paketpris upp till och med 15 lektioner.
Ekvationen bestämmer det antal lektioner där alternativen är likvärdiga.
Har du ritat graferna?
Ja, ekvationen blev ungefär x = 13,8
Så efter 13,8 körlektioner blir den sammanlagda kostnaden lika?
Man kan inte ta 13,8 lektioner så vi får avrunda.
Betydde "Ja" att du ritat graferna?
Har inte ritat graferna för vet inte hur jag ska göra 650x som linjens lutning, men har löst ekvationen
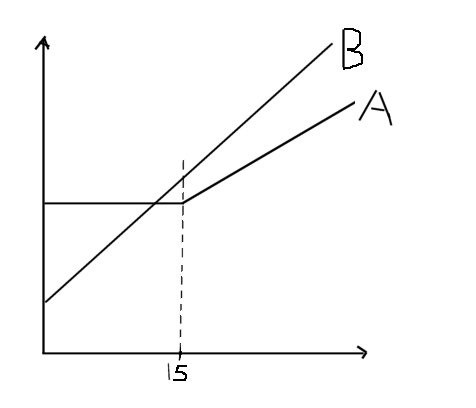
Graferna blir något åt det här hållet.
Det är bara att välja lämpliga mått på axlarna
och beräkna ytterligare en punkt på vardera linjen.
Graferna visar att x<15.
Blir då svaret på A = efter ca 13,8 körlektioner blir den sammanlagda kostnaden lika
Och sedan att körskola A blir billigare om x > 13,8 och körskola B blir billigare om x < 13,8
Ja, men som sagt måste vi avrunda.
Vid 14 lektioner är kostnaderna likvärdiga, det skiljer bara 100 kr.
Under 14 lektioner är B billigare och från och med 14 lektioner är A billigare.
Om du har facit, hur formulerar de svaret där?
Har inte facit, men tack för hjälpen!
En fråga, ska man inte använda 13500 + 500(x-15) i sin ekvation och varför tar man 13500

