Problemlösning tredjegradsekvation

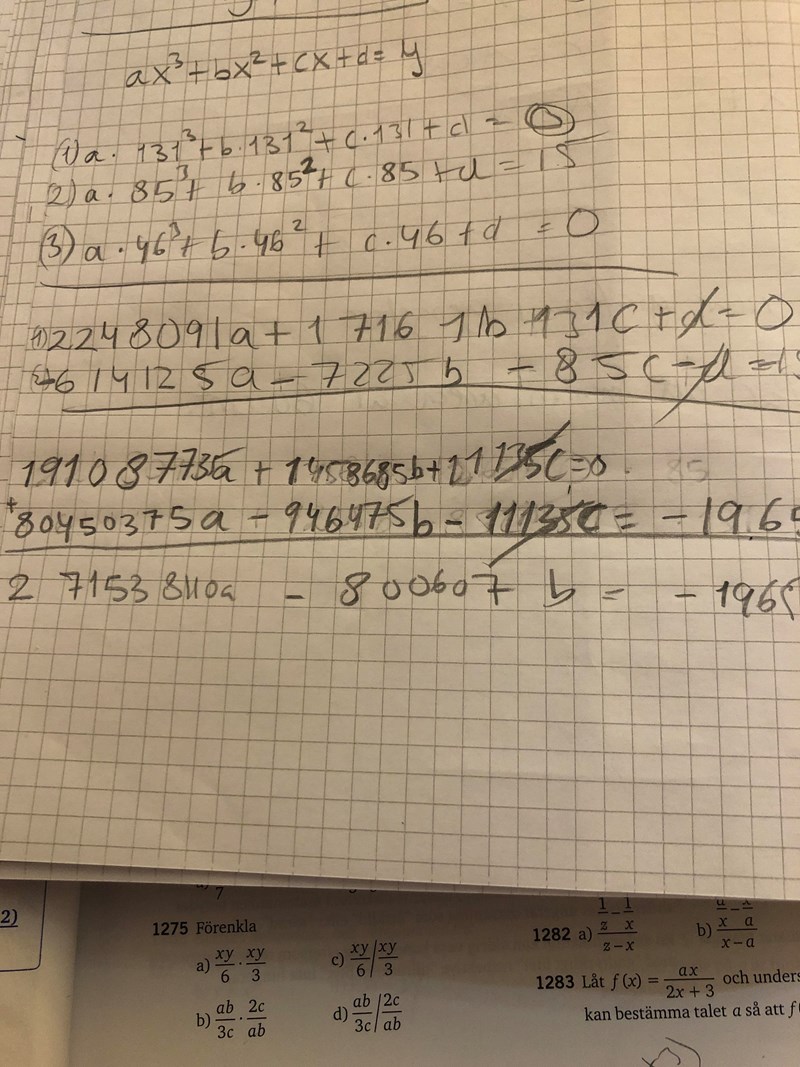
Jag hade tolkat 131 m längre fram som 131 m framför de 46. Var står det att det ska vara en tredjegradare?

Av uppgiften att döma låter det som att golfbollens bana ska likna en parabel. Med andra ord bör du nog uttrycka det som en andragradsfunktion. Det lättaste kanske är att börja med att försöka skriva en funktion som åtminstone har rätt nollställen, samt en maxpunkt.

Okej. Det ska alltså vara en andragradsfunktion. Vilka punkter ska jag isåfall använda mig av? Jag har lyckats konstanterna att en av punkterna ska vara (177,0) . Hur kan jag uttrycka punkten där y är lika med 15m. Vad är x i detta fall?

————-

Så långt har jag kommit.

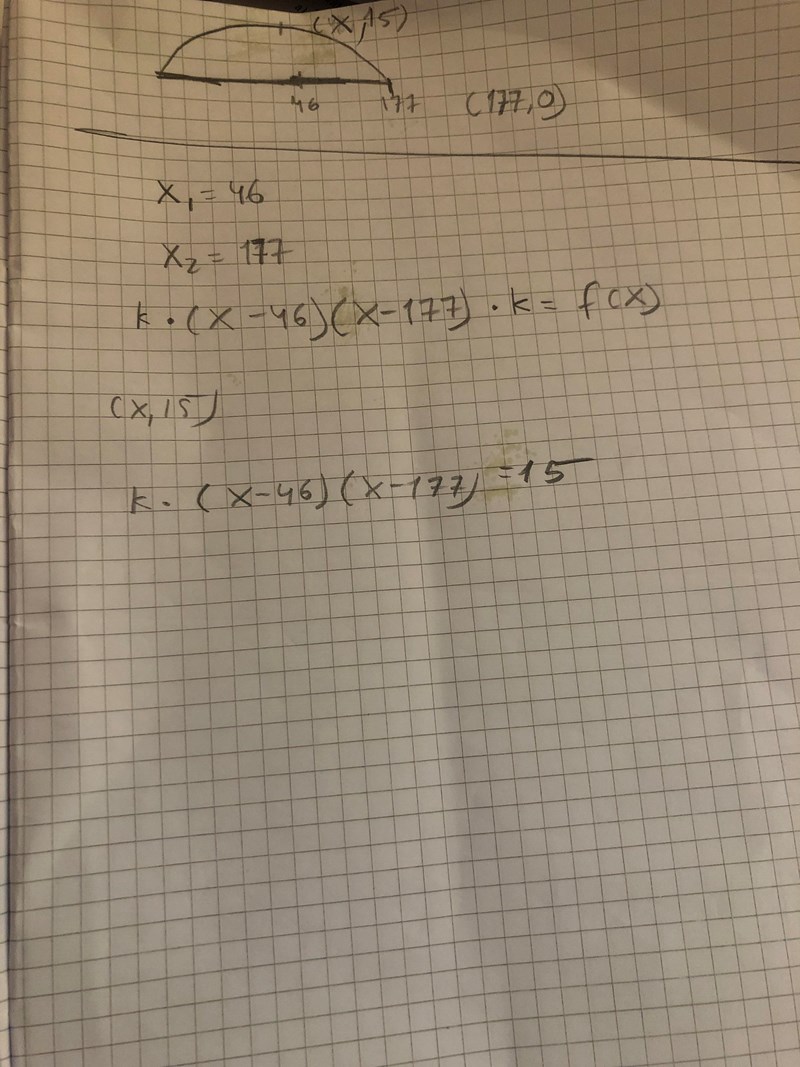
Hej S. S., 

Placera ett xy-koordinatsystem med origo $(0,0)$ vid utslagspunkten och där golfbollen rör sig i xy-planet. Då kommer y-koordinaten att beskriva bollens höjd över marken och x-koordinaten bollens förflyttning längs marken. Anta att golfbollen tar mark på samma höjd som utslagspunkten så att bollen tar mark i punkten $(131-46,0)=(85,0).$

En parabel som har nollställen när $x=0$ och $x=85$ har ekvationen

    $y(x) = k \cdot (x-0)(x-85).$

Mitt emellan de två nollställena når parabeln sin extrempunkt, vilken i detta fall ska vara en maximipunkt.  Maximipunktens x-koordinat är alltså $(0+85)/2$ och dess y-koordinat är $15$ vilket betyder att

    $15 = y(42.5) = k\cdot 42.5\cdot (42.5-85) \iff k=-\frac{15}{42.5^2}=-0.0083.$

Okej isåfall ska det bli så här : 

Jag tolkar uppgiften som att bollen går från (46,0) till (46+131,0).

Hur ska man veta vad som är rätt? Ni tolkar ju det på olika sätt?

Jag kan bara säga att jag inte har skrivit tidigare i den hrä tråden eftersom jag inte kan tolka frågan.

Laguna skrev:

Jag tolkar uppgiften som att bollen går från (46,0) till (46+131,0).

Jag tolkar texten som att alla avstånd utgår från tee. Utslagspunkten är 46 meter från tee och nedslagspunkten är 131 meter från tee. 

Vad säger facit?