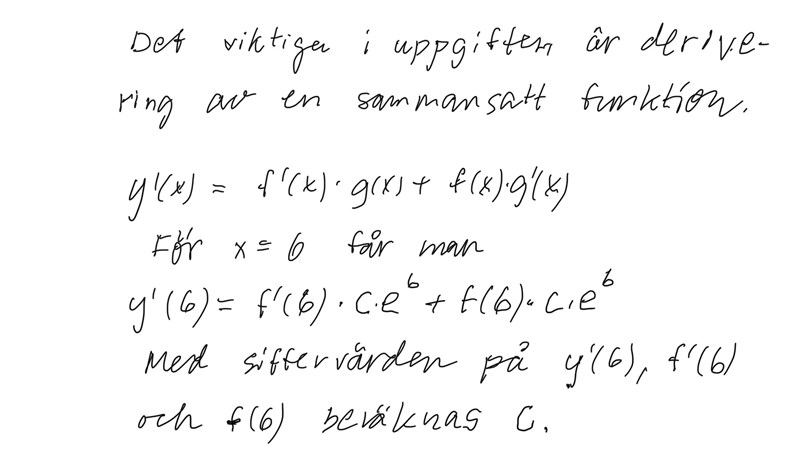Produktregeln
Hejsan!
Jag behöver lite hjälp med följande uppgift:
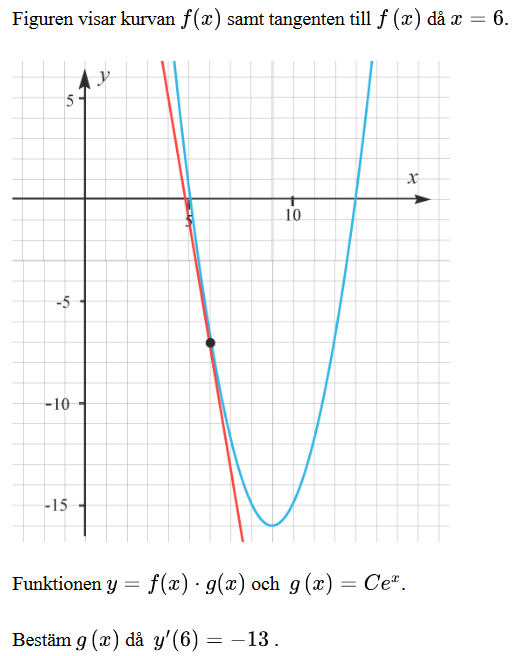
Min lärare har sakt att svaret är: g(x)=0,02ex, jag vet att jag behöver använda produktregeln men vet inte vart jag ska börja. Tack i förhand!
Välkommen till Pluggakuten! Börja med att derivera (skriv där det behövs). Sätt sedan in och på respektive ställe. Vad får du då? :)
Smutstvätt skrev:Välkommen till Pluggakuten! Börja med att derivera (skriv där det behövs). Sätt sedan in och på respektive ställe. Vad får du då? :)
Det blir:
y=f'(x)*g(x)+f(x)*g'(x)
g(x)=Cex och g'(x)=Cex
Alltså: y=f'(x)*Cex+f(x)*Cex
Vad står C för? Jag antar att det är bara ett konstant.
Genom att betrakta nollställena och minimipunkten för den blåa kurvan för f(x) kan du skriva ner hur funktionen ser ut.
Jan Ragnar skrev:Genom att betrakta nollställena och minimipunkten för den blåa kurvan för f(x) kan du skriva ner hur funktionen ser ut.
Jag kan inte klura utt det 100% men jag kan tänka mig att det är: f(x)=x+x^2- 16
HundÄlskare skrev:Jan Ragnar skrev:Genom att betrakta nollställena och minimipunkten för den blåa kurvan för f(x) kan du skriva ner hur funktionen ser ut.
Jag kan inte klura utt det 100% men jag kan tänka mig att det är: f(x)=x+x^2- 16
Nej. Det enklaste är att börja med att hitta symmetrilinjen. Var är den?
Smaragdalena skrev:HundÄlskare skrev:Jan Ragnar skrev:Genom att betrakta nollställena och minimipunkten för den blåa kurvan för f(x) kan du skriva ner hur funktionen ser ut.
Jag kan inte klura utt det 100% men jag kan tänka mig att det är: f(x)=x+x^2- 16
Nej. Det enklaste är att börja med att hitta symmetrilinjen. Var är den?
Den ligger skär mitten av kurvan: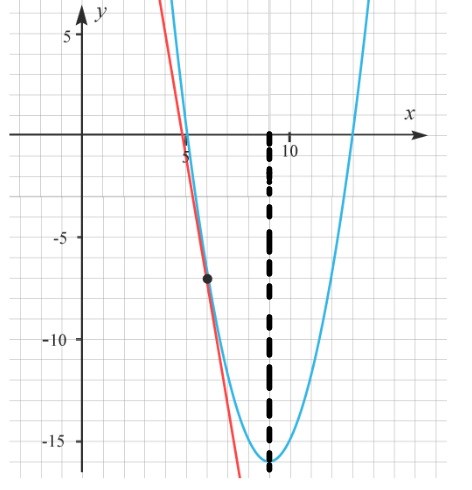 Och formler är (nollställ1+nollställ2)/2 dvs. (5+13)/2=9
Och formler är (nollställ1+nollställ2)/2 dvs. (5+13)/2=9
Så andragradsfunktionen kan skrivas som k(x-9)2+b. Om man går 1 steg åt höger från minimum så ökar funktionens värde med 1, och om man går ett steg till ökar det med 3 steg. Det visar att k = 1 så det är bara värdet på b som du behöver ta fram.
Smaragdalena skrev:Så andragradsfunktionen kan skrivas som k(x-9)2+b. Om man går 1 steg åt höger från minimum så ökar funktionens värde med 1, och om man går ett steg till ökar det med 3 steg. Det visar att k = 1 så det är bara värdet på b som du behöver ta fram.
Jag kan anta då att om y=ax^2+bx+c
Då är: ax^2=(-9x)^2 och bx=1*x
Jag tolkar det som att det är c som jag letar efter, vilken formel ska jag använda för att hitta det, eftersom när jag använder (b/2)^2 får jag 0.25 och när jag stoppar in alla siffror på ett graf får jag fel resultat
HundÄlskare skrev:Smaragdalena skrev:Så andragradsfunktionen kan skrivas som k(x-9)2+b. Om man går 1 steg åt höger från minimum så ökar funktionens värde med 1, och om man går ett steg till ökar det med 3 steg. Det visar att k = 1 så det är bara värdet på b som du behöver ta fram.
Jag kan anta då att om y=ax^2+bx+c
Då är: ax^2=(-9x)^2 och bx=1*x
Jag tolkar det som att det är c som jag letar efter, vilken formel ska jag använda för att hitta det, eftersom när jag använder (b/2)^2 får jag 0.25 och när jag stoppar in alla siffror på ett graf får jag fel resultat
För att förtydliga
Enligt mig:
a=-9
b=1
c=?
c=(b/2)^2
Dock får jag ett svar som är inte korrekt
Nej, om koefficienten för kvadrattermen är negativ har vi ett maximivärde ("sur mun"), inte ett minimum.
OK, vi kan ansätta att y = ax2+bx+c istället - det blir krångligare men det funkar. Vi kan läsa av tre punkter i bilden, t ex (5,0), (9,-16) och (13,0). Då får vi ekvationssystemetsom man kan lösa med sedvanliga metoder.
Alternativt kan man skriva andragradsfunktionen som y = (x-9)2-16, där man lätt läser av att minimivärdet är -16 i bilden (och att koefficienten för kvadrattermen är 1 beskrev jag i mitt förra inlägg). Om vi multiplicerar ihop detta får vi y = x2-18x+81-16 eller y = x2-18x+65.
Smaragdalena skrev:Nej, om koefficienten för kvadrattermen är negativ har vi ett maximivärde ("sur mun"), inte ett minimum.
OK, vi kan ansätta att y = ax2+bx+c istället - det blir krångligare men det funkar. Vi kan läsa av tre punkter i bilden, t ex (5,0), (9,-16) och (13,0). Då får vi ekvationssystemetsom man kan lösa med sedvanliga metoder.
Alternativt kan man skriva andragradsfunktionen som y = (x-9)2-16, där man lätt läser av att minimivärdet är -16 i bilden (och att koefficienten för kvadrattermen är 1 beskrev jag i mitt förra inlägg). Om vi multiplicerar ihop detta får vi y = x2-18x+81-16 eller y = x2-18x+65.
Juste, tackar!
Nu när vi har f(x) då är det bara att sätta in det i funktionen:
HundÄlskare skrev:Smaragdalena skrev:Nej, om koefficienten för kvadrattermen är negativ har vi ett maximivärde ("sur mun"), inte ett minimum.
OK, vi kan ansätta att y = ax2+bx+c istället - det blir krångligare men det funkar. Vi kan läsa av tre punkter i bilden, t ex (5,0), (9,-16) och (13,0). Då får vi ekvationssystemetsom man kan lösa med sedvanliga metoder.
Alternativt kan man skriva andragradsfunktionen som y = (x-9)2-16, där man lätt läser av att minimivärdet är -16 i bilden (och att koefficienten för kvadrattermen är 1 beskrev jag i mitt förra inlägg). Om vi multiplicerar ihop detta får vi y = x2-18x+81-16 eller y = x2-18x+65.
Juste, tackar!
Nu när vi har f(x) då är det bara att sätta in det i funktionen:
Efter det är det att använda
Jag vet inte hur jag kan bevisa att
Det saknas något på min sida som jag kan förstå, förmodligen något extremt enkelt för att slutföra uppgiften. :)
Man kan ju läsa av f(6) och f'(6) i bilden, så man behöver inte ta fram f(x) alls.
Tillägg: 22 maj 2022 10:48
f(6) utlästes från grafen
f'(6) utlästes från grafen , negativ lutning
Jag är helt borta nu, om svaret är , hur ska jag tillämpa den? Jag har ingen anning vad är nästa steg nu när C är löst.
HundÄlskare skrev:Jag är helt borta nu, om svaret är , hur ska jag tillämpa den? Jag har ingen anning vad är nästa steg nu när C är löst.
Läs igenom uppgiften. Vad är det man frågar efter?
Smaragdalena skrev:HundÄlskare skrev:Jag är helt borta nu, om svaret är , hur ska jag tillämpa den? Jag har ingen anning vad är nästa steg nu när C är löst.
Läs igenom uppgiften. Vad är det man frågar efter?
Bestäma när
Ålltså hitta en variabel för (x) när funktionen av
HundÄlskare skrev:Smaragdalena skrev:HundÄlskare skrev:Jag är helt borta nu, om svaret är , hur ska jag tillämpa den? Jag har ingen anning vad är nästa steg nu när C är löst.
Läs igenom uppgiften. Vad är det man frågar efter?
Bestäma när
Ålltså hitta en variabel för (x) när funktionen av
Där funktionen av
Nej, du skall beräkna y-värdet för g(x) när y' = -13.
Vad är y'(x)?
Vad är y'(6)?
Smaragdalena skrev:Nej, du skall beräkna y-värdet för g(x) när y' = -13.
Vad är y'(x)?
Vad är y'(6)?
y'(x)=f'(x)*g(x)+f(x)*g'(x)
y'(6)= -13 alltså att vi måste lösa C
Hur är det då att g(x)=0,02ex?
Är det eftersom ?
HundÄlskare skrev:Smaragdalena skrev:Nej, du skall beräkna y-värdet för g(x) när y' = -13.
Vad är y'(x)?
Vad är y'(6)?
y'(x)=f'(x)*g(x)+f(x)*g'(x)
y'(6)= -13 alltså att vi måste lösa C
Hur är det då att g(x)=0,02ex?
Är det eftersom ?
Det verkar vara korrekt svar men jag vet inte hur svaret 0,02ex är korrekt.
Då blir det istället g(x)=0,002ex