Produktregeln på divergens av skalär och vektor

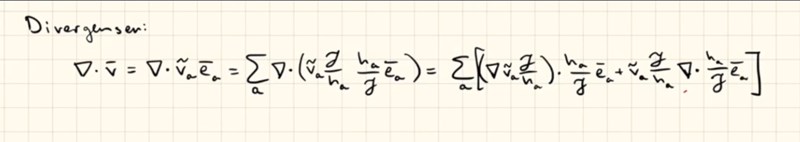
Lite oklart vad du vill.

Vill du visa att $\nabla \bullet \left(\varphi \overrightarrow{v}\right)=\nabla \varphi \bullet \overrightarrow{v}+\varphi \nabla \bullet \overrightarrow{v}$?

Hej,

Varför multiplicerar man med

    $1 = \frac{J}{h_\alpha} \cdot \frac{h_\alpha}{J}$

i det hela?

Vad betecknar $J$?

Vad betecknar $h_\alpha$?

Du har inte gett något sammanhang, utan bara lösryckt presenterat påstådd beräkning av divergens.

Jag förstår inte varför man inte nöjer sig med

    $\nabla \cdot v = \partial _\alpha v^{\alpha}.$

Är det för att man vill uttrycka divergensen i godtyckliga kurvilinjära koordinater?

PATENTERAMERA skrev:

Lite oklart vad du vill.

Vill du visa att $\nabla \bullet \left(\varphi \overrightarrow{v}\right)=\nabla \varphi \bullet \overrightarrow{v}+\varphi \nabla \bullet \overrightarrow{v}$?

Hmmm, just det, man kan ju visa det och byta ut $\varphi$, det sambandet har jag visat förut

Albiki skrev:

Hej,

Varför multiplicerar man med

    $1 = \frac{J}{h_\alpha} \cdot \frac{h_\alpha}{J}$

i det hela?

Vad betecknar $J$?

Vad betecknar $h_\alpha$?

Du har inte gett något sammanhang, utan bara lösryckt presenterat påstådd beräkning av divergens.

Jag förstår inte varför man inte nöjer sig med

    $\nabla \cdot v = \partial _\alpha v^{\alpha}.$

Är det för att man vill uttrycka divergensen i godtyckliga kurvilinjära koordinater?

Aaa precis så inte bara för kartesiska som är div $\overrightarrow{v}=a_i{v}^i$

För att kunna ge dig hjälp på rätt nivå kan det vara bra att få veta vilken kurs du läser. Det ser ut som att du försöker tillämpa Voss-Weyl, men om ni gått igenom den affina kopplingen är det lättare att bara följa produktregeln för partiell kovariant derivata.

Den kovarianta derivatan av en produkt av två godtyckliga tensorfält är formellt identisk med den vanliga produktregeln som gäller vid partiell differentiering.

$\nabla_k(\Phi v^j)=(\Phi v^j)_{|k}=(\Phi)_{|k}v^j+\Phi v^j_{|k}$

Jämför med hur man deriverar $D(fg)=f'g+fg'$. Nu kontraherar vi över indexen $k,j$ sätt $k=j=r$ för att få divergensen:

$\nabla\cdot (\Phi\vec{v})=(\Phi v^r)_{|r}=\frac{\partial \Phi}{\partial u^r}v^r+\Phi v^r_{|r}=\nabla\Phi\cdot \vec{v}+\Phi\nabla\cdot \vec{v}$

Med beteckningen $X^j_{|k}$ menas alltså $X^j_{|k}=\frac{\partial X^j}{\partial u^k}+\Gamma^j_{mk}X^m$.