Prov fråga - polynomkonstruktion med bestämda asymptoter
Skapa en funktion f(x) på formen p(x)/q(x) där p(x) och q(x) är polynom. f(x) ska ha asymptoterna x=3 och y=2x+3. Den får ej ha extrempunkter, alltså f'(x)≠0. Jag är övertygad att detta inte är möjligt.
2x + 3 + 1/(x-3) fungerar ju inte även om man gör om det till ((2x+3)(x-3)+1)/(x-3) eftersom dess derivata kommer ha nollställen och därmed finns det ju extrempunkter.
Snälla hjälp!
Smart fråga. Det är möjligt.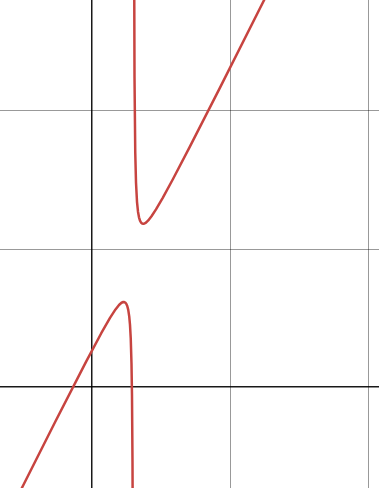 
Om aldrig är 0 vill vi att derivatan alltid ska vara positiv eller negativ. Då måste funktionen alltid vara växande/avtagande. -delen kommer alltid ha en positiv derivata. Det vi saknar är därmed funktion som har en asymptot som har positiv derivata (är växande).
AlexMu skrev:Smart fråga. Det är möjligt.
Om aldrig är 0 vill vi att derivatan alltid ska vara positiv eller negativ. Då måste funktionen alltid vara växande/avtagande. -delen kommer alltid ha en positiv derivata. Det vi saknar är därmed funktion som har en asymptot som har positiv derivata (är växande).
Vad hade den funktionen varit isåfall?? Jag vet inte hur jag ska komma fram till ett svar. Jag är nog för frustrerad. Hade uppskattat ett rakt svar med en funktion och en förklaring.
Nootato skrev:AlexMu skrev:Smart fråga. Det är möjligt.
Om aldrig är 0 vill vi att derivatan alltid ska vara positiv eller negativ. Då måste funktionen alltid vara växande/avtagande. -delen kommer alltid ha en positiv derivata. Det vi saknar är därmed funktion som har en asymptot som har positiv derivata (är växande).
Vad hade den funktionen varit isåfall?? Jag vet inte hur jag ska komma fram till ett svar. Jag är nog för frustrerad. Hade uppskattat ett rakt svar med en funktion och en förklaring.
Delen 2x+3 har vi funnit. Vi skall nu finna delen som har
vertikal asymptot för x=3
är strängt växande
studera 1/x
vilken är dess vertikala asymptot och hur kan den modifieras för att få den för x=3
är den stängt växande? Om inte, hur kan vi modifiera den (med ett tecken) så den blir det?
Trinity2 skrev:Nootato skrev:AlexMu skrev:Smart fråga. Det är möjligt.
Om aldrig är 0 vill vi att derivatan alltid ska vara positiv eller negativ. Då måste funktionen alltid vara växande/avtagande. -delen kommer alltid ha en positiv derivata. Det vi saknar är därmed funktion som har en asymptot som har positiv derivata (är växande).
Vad hade den funktionen varit isåfall?? Jag vet inte hur jag ska komma fram till ett svar. Jag är nog för frustrerad. Hade uppskattat ett rakt svar med en funktion och en förklaring.
Delen 2x+3 har vi funnit. Vi skall nu finna delen som har
vertikal asymptot för x=3
är strängt växande
studera 1/x
vilken är dess vertikala asymptot och hur kan den modifieras för att få den för x=3
är den stängt växande? Om inte, hur kan vi modifiera den (med ett tecken) så den blir det?
Nej men lägg av är det så lätt. Det är ju bara att ta -1/(x-3) för att istället få en funktion där den alltid ökar och på så sätt får man en derivata vars värde aldrig kan vara noll eftersom den alltid håller sig på en sida av x-axeln.
Tack för hjälpen! Jag är riktigt frustrerad att jag inte fattade det under provet.
