Pust. Fortfarande problem med gränser
En roaming och återkommande tema i livet.
Men nu har jag problemet:

Jag förstår inte den här grej med att etablera inre gränser med en funktion. Jag försökte detta. Dr. G och andra optiker får ursäkta mig för en ful representation av :
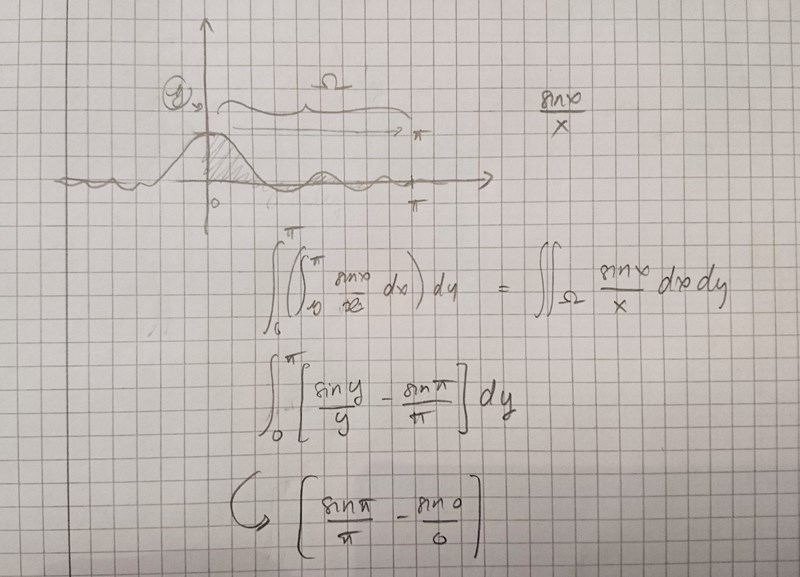
Jag får noll när jag ser på bilden att ... det är åtminstone 1.
Jag försökte förresten rita den i mathematica, kan ni berätta vad är fel i koden? Jag testade olika varianter med Integrate, NIntegrate osv.

Hej!
där indikatorfunktionen när och lika med noll för alla andra .
Det går ju inte att hitta en elementär primitiv funktion till . Alltså får vi försöka ändra ordning på variablerna och hoppas att vi får en enklare integral. För att göra det behöver vi se hur området ser ut.
Jag vet inte vad du försöker rita, men vi är ju intresserade av området vi integrerar över. Detta område har ingenting med att göra, utan är en triangel definierat av olikheterna och :

Försök nu ställa upp integralens gränser med innerst utifrån detta område.
Förlåt, kan du förklara för mig hur du sätter dessa gränser? Varför y är mindre än x?
Det ser man ju på integrationsgränserna. Integralen i -led har gränserna och . Då varierar ju mellan och , d.v.s. . På samma sätt går -integralen från till , och därför blir det .
Hej Daja,
Den första integrationsgränsen säger att x ska gå från y till . Om man vill kan man skriva det som .
Den andra integrationsgränsen säger att y ska gå från 0 till . Om man vill kan man skriva det som .
Om vi sammanfattar ska du alltså integrera över området
Kan du försöka rita upp det området?
Angående Mathematica är det så att hon tolkar den första gränslistan du matar in som den yttre integralen och så fortsätter det inåt.
Din integral ges alltså av:
Integrate[Sin[x]/x, {y, 0, \[Pi]}, {x, y, \[Pi]}]
Som Alvin ritade:
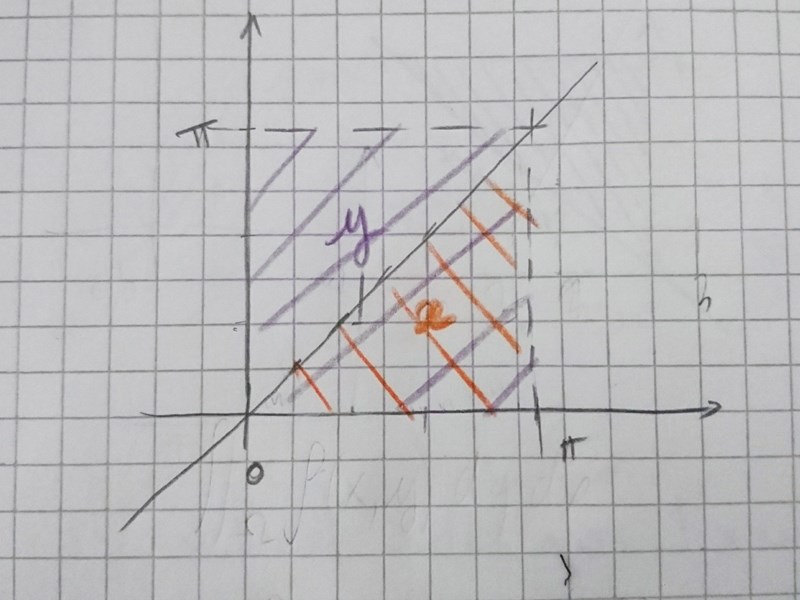
Måste det vara trianglet orange OCH lilla?
Trycker skamlöst upp mitt ful område för checkande ...




