pyramid
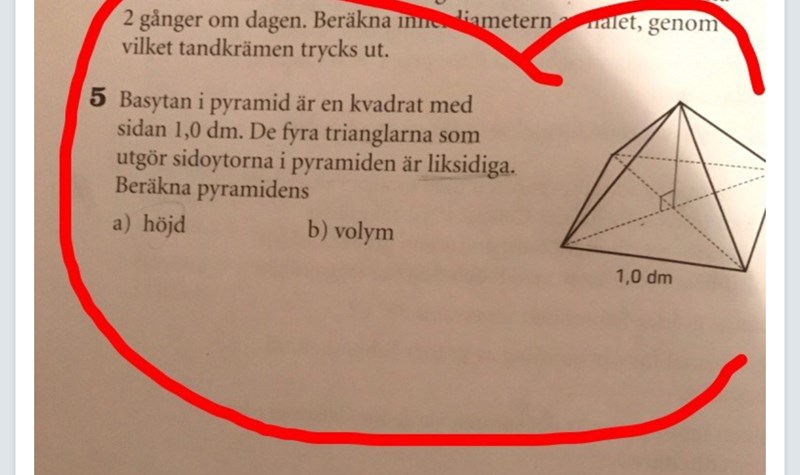
Jag har fastnat på up 5a.
Min lösning hitils :
x är sidan av de likbenta trianglarna i figuren.
x^2+x^2=1^2
x=0,7dm
alltså är en av kateten för triangeln 0,7dm. Triangelns höjd är H. Men hur kan jag ta reda på hur lång hypotenusan är?
Renny19900 skrev:
Jag har fastnat på up 5a.
Min lösning hitils :
x är sidan av de likbenta trianglarna i figuren.
x^2+x^2=1^2
x=0,7dm
alltså är en av kateten för triangeln 0,7dm. Triangelns höjd är H. Men hur kan jag ta reda på hur lång hypotenusan är?
Nej det står att sidoytorna utgörs av liksidiga (inte likbenta) trianglar.
Dessutom kan du endast använda Pythagoras sats på rätvinkliga trianglar.
Pröva att istället se pyramiden "snett" från sidan (så att du kikar längs med en kant och endast ser 2 av de 4 sidoytorna).
Rita en figur och visa.
Förlåt, jag menade likbenta trianglar.
Jag förstår dock inte hur jag ska beräkna höjden?
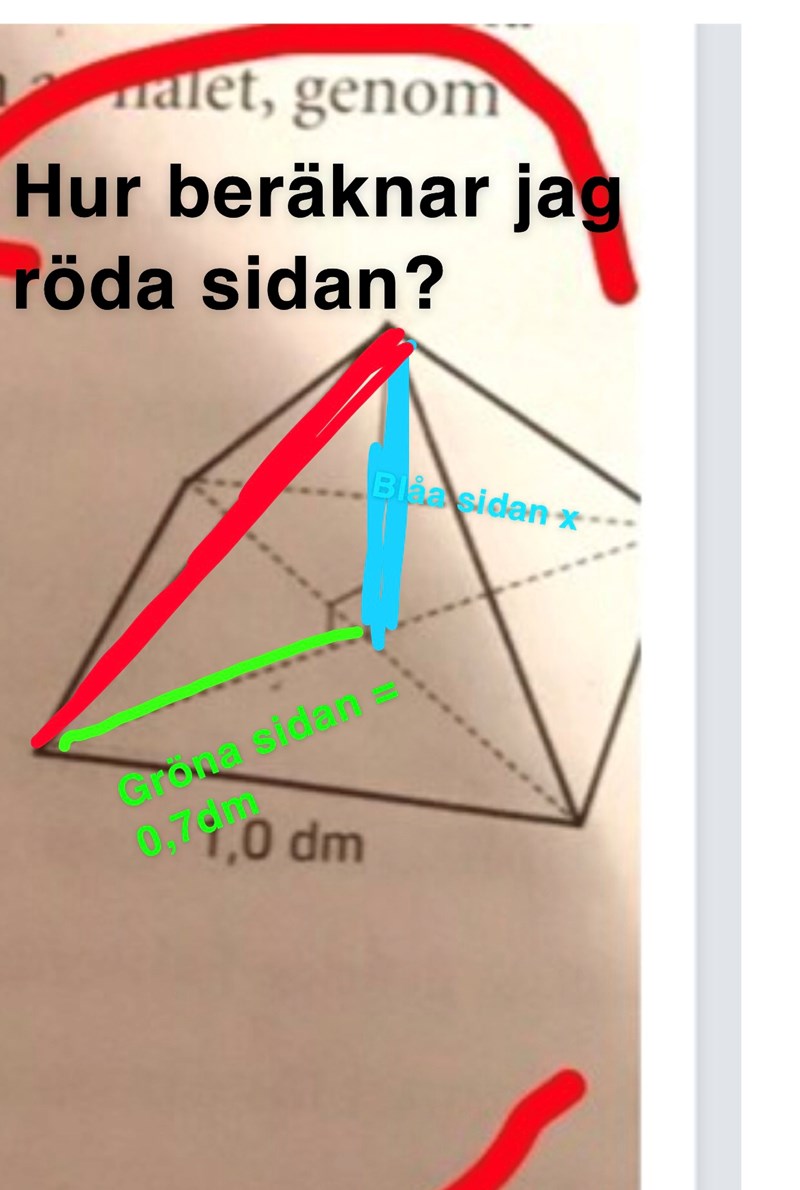
Renny19900 skrev:Förlåt, jag menade likbenta trianglar.
Jag förstår dock inte hur jag ska beräkna höjden?
Bra figur! Jättetydlig!
Vad är vinkeln mellan den gröna och den blå sträckan?
Du vet hur lång den röda sträckan är eftersom den är en av kanterna i den liksidiga triangeln som utgör en av pyramidens sidoytor (nu skrev du likbent igen).
Jag vet faktiskt inte hur röda sidan kan vara 1dm. Derkänns konstigt eftersom det bara är basytans sidor som är 1dm. Har inte lyckats lösa ut hypotenusa (röda sidan)
det är 90 grader??
Yngve skrev:Renny19900 skrev:Förlåt, jag menade likbenta trianglar.
Jag förstår dock inte hur jag ska beräkna höjden?
Bra figur! Jättetydlig!
Vad är vinkeln mellan den gröna och den blå sträckan?
Du vet hur lång den röda sträckan är eftersom den är en av kanterna i den liksidiga triangeln som utgör en av pyramidens sidoytor (nu skrev du likbent igen).
Hur ser du att sidan är liksidig? Jag ser att det är en likbent triangel som hypotenusan utgör
Renny19900 skrev:Hur ser du att sidan är liksidig? Jag ser att det är en likbent triangel som hypotenusan utgör
Jag ser inte att den är liksidig, det står i uppgiften att den är det.
Läs igen, väldigt långsamt:
De fyra trianglarna som utgör pyramidens sidoytor är liksidiga.
En triangel är liksidig då alla dess sidor är lika långa.
En triangel är likbent då (åtminstone) två av dess sidor är lika långa.
----
Och ja, det stämmer att det är en rät vinkel mellan den gröna och den blå sträckan.
-----
Det här är alltså en liksidig triangel.
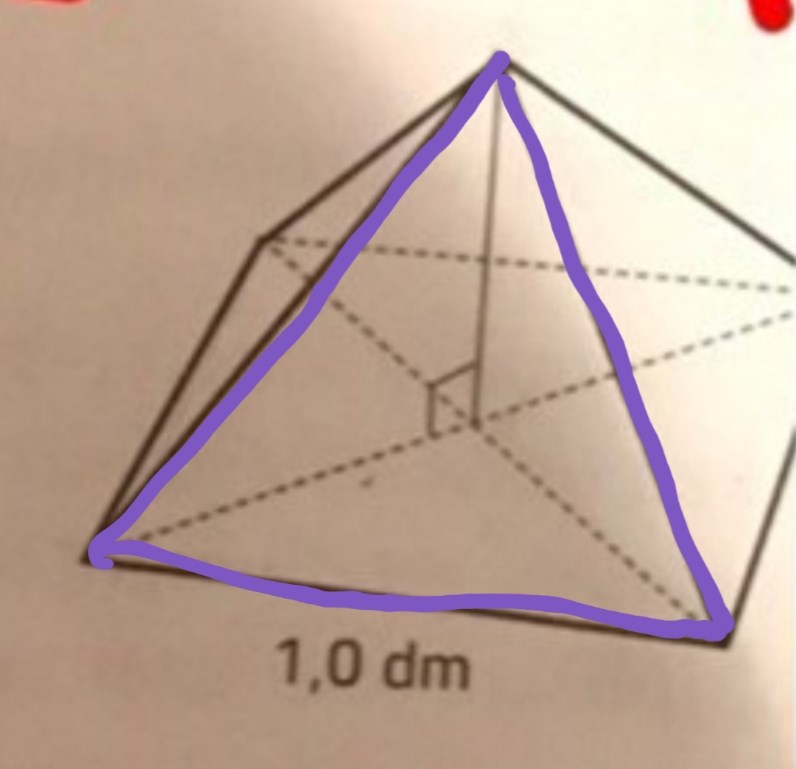
Okej då är hypotenusa 1dm
ekvationen blir då
1^2=h^2+0,7^2
h=0,71dm (avrundat)
stämmer det? (h=höjden)
Renny19900 skrev:Okej då är hypotenusa 1dm
ekvationen blir då
1^2=h^2+0,7^2
h=0,71dm (avrundat)
stämmer det? (h=höjden)
Ja det stämmer.


