Pythagoras sats uppgift!
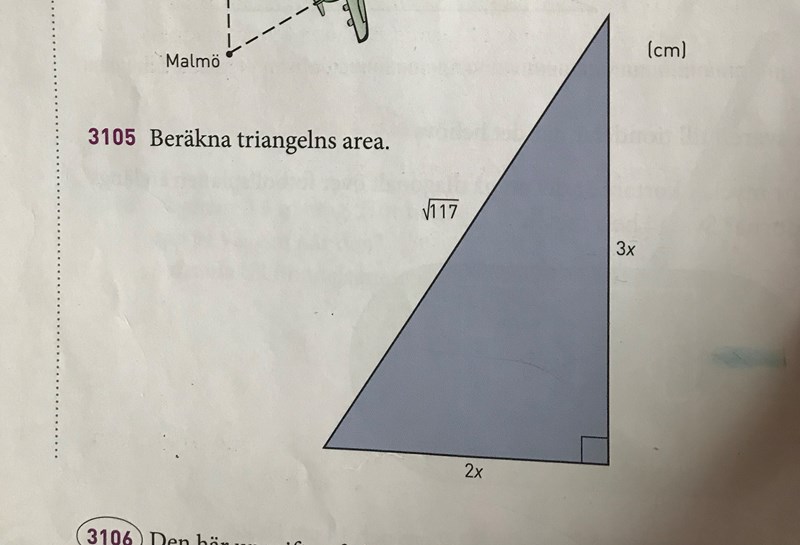 Jag tänkte såhär: 3x upphöjt till 2 + 3x upphöjt till 2 = roten ur 117
Jag tänkte såhär: 3x upphöjt till 2 + 3x upphöjt till 2 = roten ur 117
9x + 4x = roten ur 117
13x = roten ur 117
X = 10,8166..
Jag fattar inte hur jag ska gå vidare..
Inte riktigt rätt användning av satsen som säger , där a & b är kateter och c är hypotenusan.
I den här uppgifter får vi då . Hur förenklar man denna ekvation? Du är på rätt spår men glöm inte att inte bara tvåan och trean ändras, x ändras också. Och vad händer om man tar roten ur ett tal, och sen upphöjt i två?
På svar till hur du ska gå vidare så är det du letar efter triangelns area, vilket är basen gånger höjden ().
I ditt fall är basen 2x och höjden 3x.
Räkna ut enligt jakobpwns svar.
Jag gjorde de men det funkar inte riktigt.
Jag tänkte vidare såhär: 5x upphöjt till 2 delat på 5 = 117 upphöjt till 2 delat på 5
x upphöjt till 2= 117 delat på 5
roten ur 117/5 blir fel svar
(3x)2 + (2x)2 = ()2
9x2 + 4x2 = 117
13 x2 = 117
x2 = 9
Area: 2x*3x/2 = 3x2 = 3*9 = 27 cm2
Du kan få fram x genom att använda pytagoras sats, så här:
(2x)2+(3x)2 =
sen är det viktigt att tänka på att:
(2x)2 = 22*x2 = 4x2
och att
Louis jag förstod inte hur du kom fram till
9, 117/13? Varför då?
Ska man inte använda roten ur för
att ta reda på vad x är?
Louis räknade ut vad är, och ja de använde 117/13. För att få x tar man alltså roten ur 9, men det visar sig att det räcker att veta vad är för att det är den som används i areaberäkningen.
Det kan man göra, men eftersom x2 i denna uppgift ska användas i beräkningen av arean är det onödigt.
Du kan skriva x = 3, och sedan kvadrera tillbaka till 9 när du räknar ut arean och med så enkla siffror blir det ingen större skillnad i ansträngning. Ändå lite onödigt tyckte jag.
Är du med på beräkningarna i övrigt?



