Räkna cos(180-v) mha enhetscirkel

Projicera sin(v) på rätt axel. Vilken axel är det?

Om sin(v) = 0,8, vilken/vilka kvadranter är v i då?

Beroende på vilken kvadrant v är i, vilken kvadrant ligger 180-v i?

Vad blir motsvarande cos-värde?

Sin(v)=0.8 ger vinkeln v 53 grader. Vilket är i första kvadranten 

Om du projicerar värdet 0,8 in på rätt axel så kommer du att se att det finns en vinkel till. 

Ja, en vinkel i andra kvadranten

Javisst. Rita in den vinkeln också i enhetscirkeln. Dra sedan räta linjer mot x- och y-axeln. Ser du nu hur du beräknar cos(180-v) för de båda alternativen för v ? Du ska alltså inte använda kalkylatorn, att beräkna värdet på v ger bara ett approximativt värde. Du kan beräkna cos-värdet utan att veta v.

ostertalje skrev:

Om du projicerar värdet 0,8 in på rätt axel så kommer du att se att det finns en vinkel till. 

Hur ritar man 0.8 i en enhetscirkel? Hur tolkar man det värdet när man ska rita det i enhetscirkel?

Okej, lite repetition om enhetscirkeln. Vad representerar y1 resp x1 för värde? Hur lång är radien? Om du vet y1, hur kan du då beräkna x1 ?

Glömde figuren:

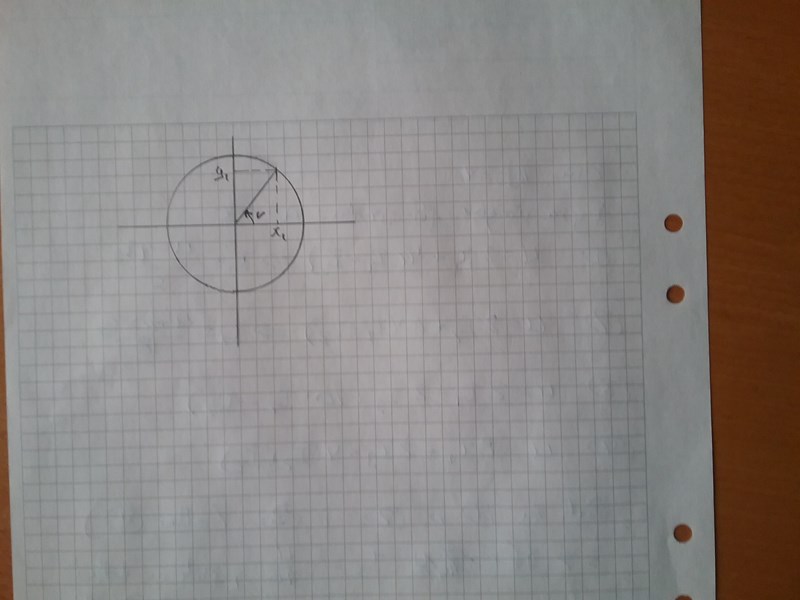
x1 = cos v 

y1=sin v

Så om cos v=0.8 så betyder det att x värdet är 0.8. 
om sin v=0.8 då betyder det att y värdet är 0.8. Eftersom att det är en enhetscirkel så är radien i cirkeln alltid 1. Vinkeln v kan därav beräknas mha trigonometri 

tan (v)=(0.8)/1=0.8

artan(0.8)=38.65 grader. 

cos(180-38.65) ska man slå detta på miniräknare?

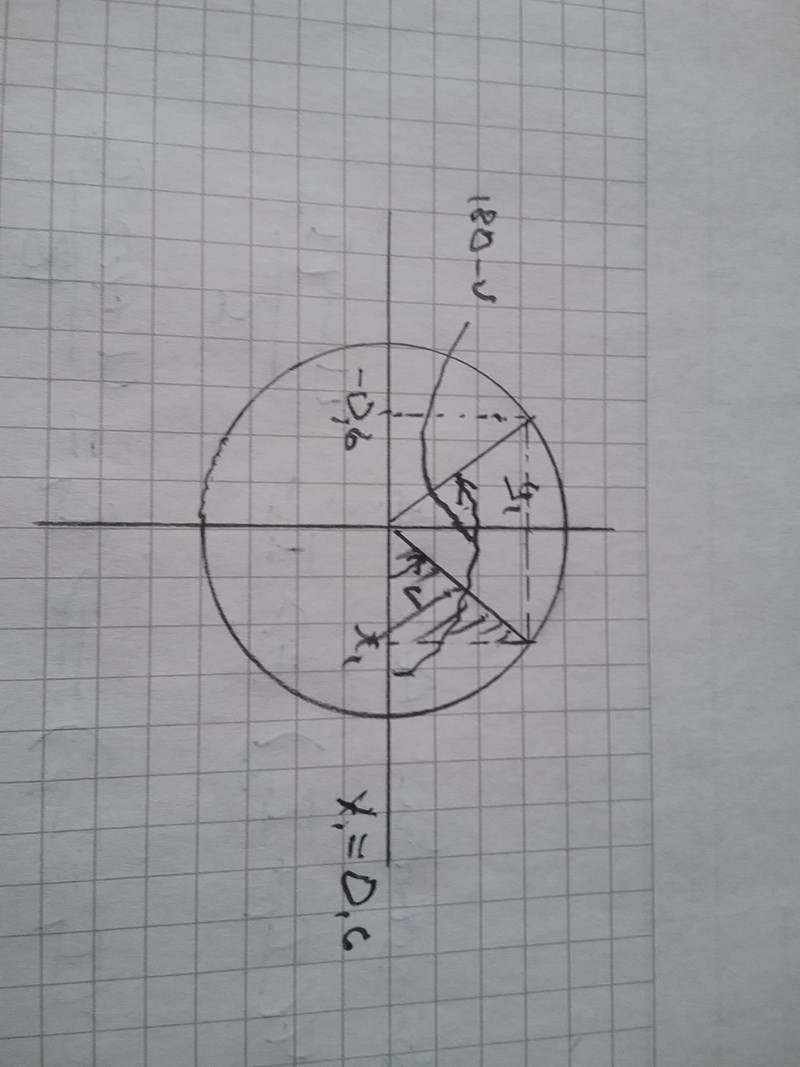
Det står att du ska använda enhetscirkeln, dvs inte trigonometri. Titta på triangeln som jag har streckat. Den är rätvinklig. Ger det dig någon ledtråd hur du ska beräkna x1 ?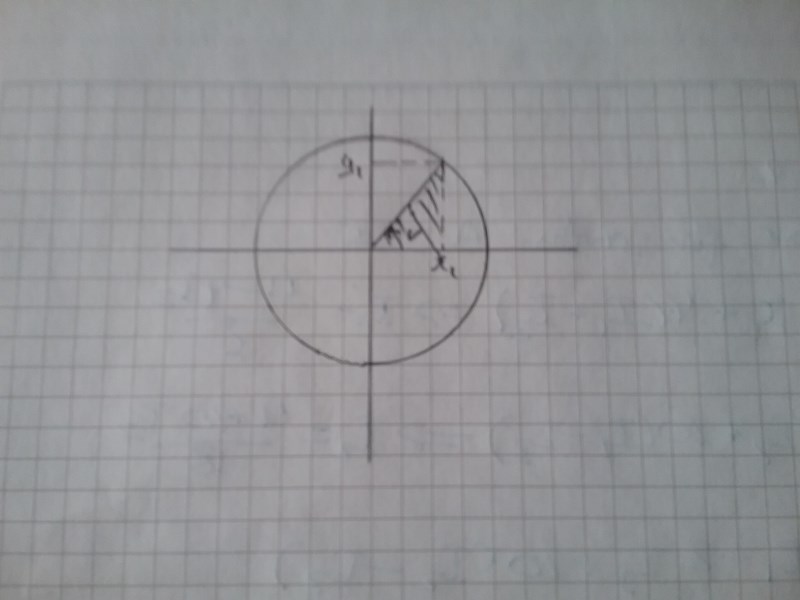

Ska det inte vara 

0.8/1 =tan (v)?

? Eller hur menar du? Hur ska jag använda mig utav enhetscirkeln

Du har en rätvinklig triangel som jag streckat. Hur lång är hypotenusan? En kateter är också känd, hur lång är den? Hur lång är då den andra katetern?

Ena kateten är 0.8 

Eftersom att det är en enhetscirkel bör hypotenusan vara 1. Alltså kan den andra kateten beräknas på följande sätt

x^2 + (0.8)^2=1^2

x=0.6 

alltså är den andra kateten 0.6 

sin v anger y värdet.

alltså 

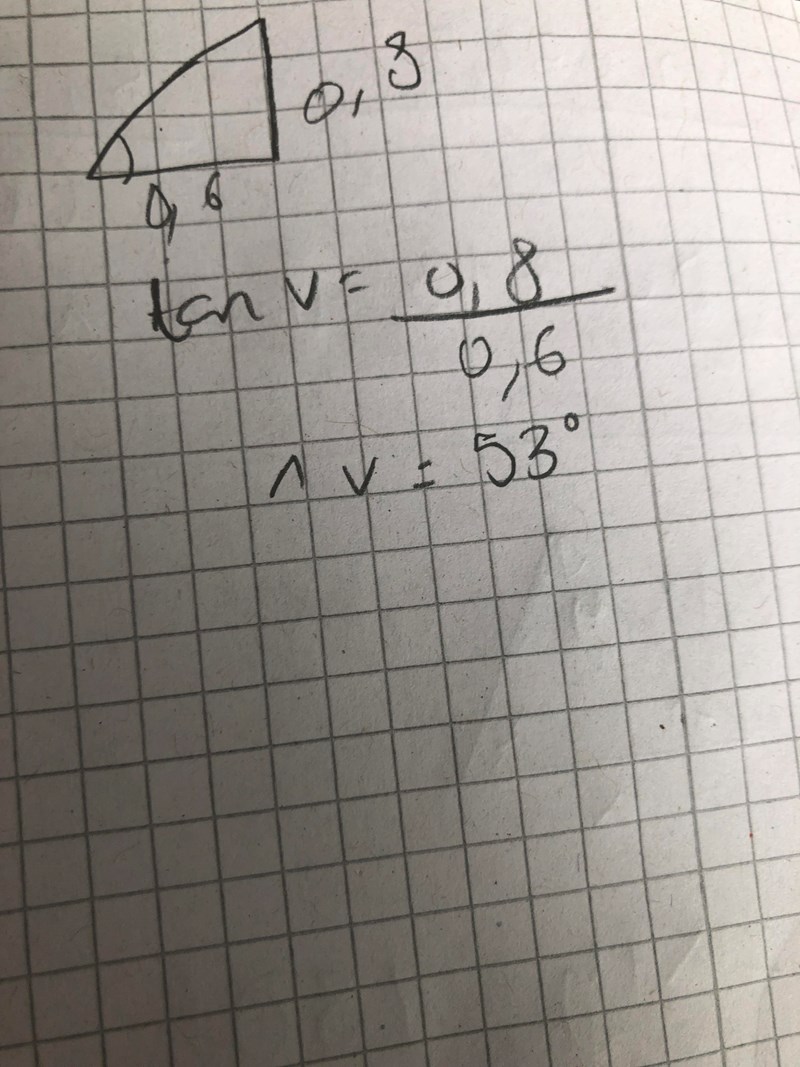
Vad bra! Om dom hade frågat efter cos(v) så hade lösningen varit enkel, eller hur? Men nu frågar dom efter cos(180-v). Vilken vinkel är det? Kan du rita ut den i figuren som jag ritat.

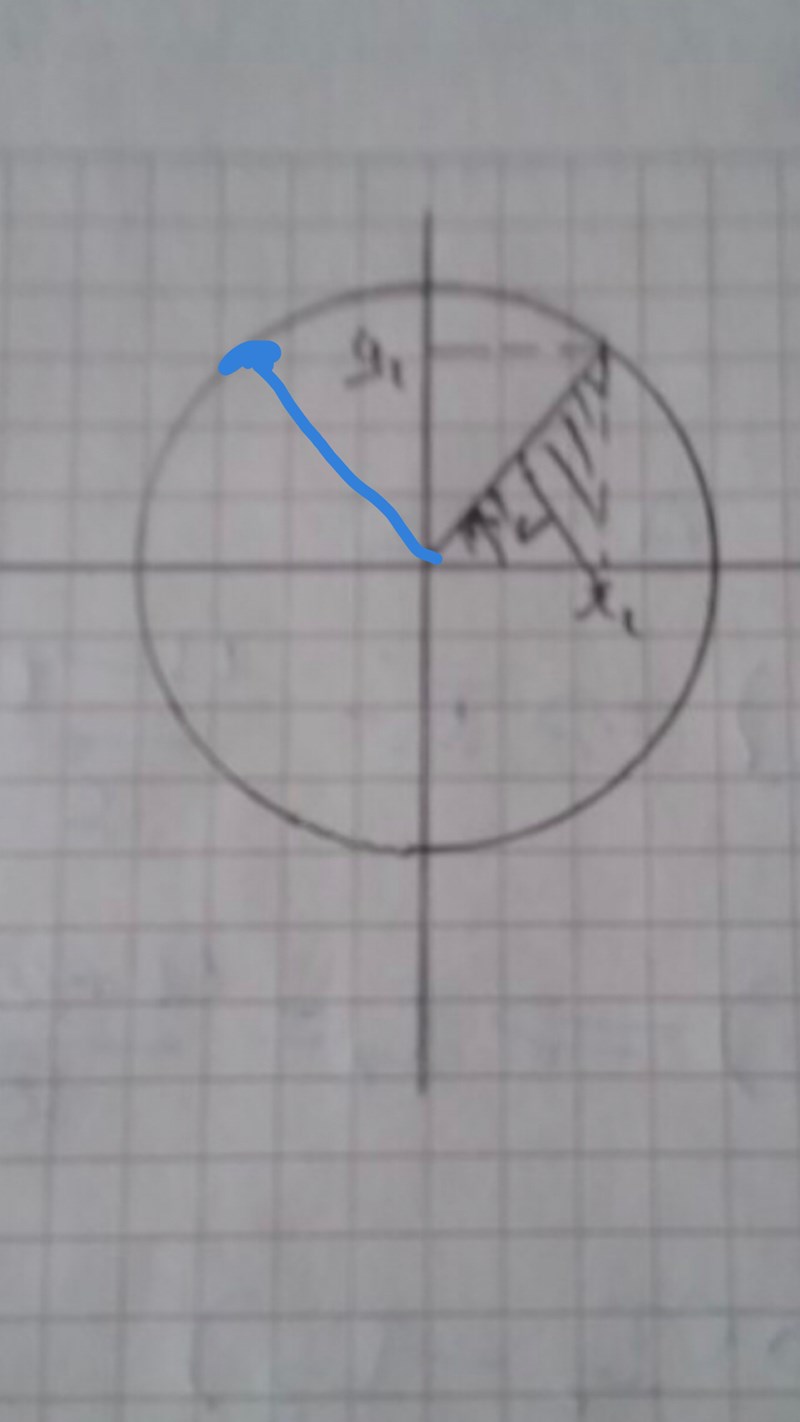Cos(180-v) ger ju oss istället y värdet 0.8 men x värdet -0.6 

Alltså blir vinkeln

0.8/(-0.6)=-53 grader ...? Varför är det minus

Och cos(180-v) blir ?

Ska jag skriva in det på miniräknaren eller? Dvs

cos(180-53)=

arcos ger 126 grader

Som jag har skrivit ovan så behöver du inte ta reda på hur stor vinkeln är. Det är bara cos(180-v) som ska bestämmas och det blir mycket riktigt -0,6 precis som du skrivit. Strunta i hur stor vinkeln är för det frågas det inte efter.

Som det är ritat så ligger v i första kvadranten men v kan vara så stor att den hamnar i andra kvadranten. Vilken vinkel är det då som blir 180-v ? (sin v ska fortfarande vara = 0,8)

Vad blir cos(180-v) om v ligger i andra kvadranten? 

ostertalje skrev:

Som jag har skrivit ovan så behöver du inte ta reda på hur stor vinkeln är. Det är bara cos(180-v) som ska bestämmas och det blir mycket riktigt -0,6 precis som du skrivit. Strunta i hur stor vinkeln är för det frågas det inte efter.

Som det är ritat så ligger v i första kvadranten men v kan vara så stor att den hamnar i andra kvadranten. Vilken vinkel är det då som blir 180-v ? (sin v ska fortfarande vara = 0,8)

Vad blir cos(180-v) om v ligger i andra kvadranten? 

Förlåt men jag förstår inte riktigt din bild... Och vet inte riktigt hur jag ska tänka att räkna cos(180-v)..

Du skulle ju inte använda miniräknaren 😀 men cos(180-v) har en lösning till förutom -0,6. 

Försök hitta den.

Ska det vara 0.6 och -0.6?

Javisst, bra ! Du har löst det.

Repetera gärna hur man läser av sin och cos i enhetscirkeln. Jag tycker enhetscirkeln är bra för förståelsen av sin sin och  cos för att det är en figur som man kan peka i. Man lätt se vad sin och cos har för tecken i resp kvadrant och t x att sin(v) = sin(180-v) och cos(v) = -cos(180-v) osv

Varför är det fel att bara svara -0.6? Kan du förklara med hjälp av din ritade bild?

sin(v1) = sin(v2) = 0,8 dvs vinkeln kan ligga både i första och andra kvadranten precis som du skrivit tidigare i tråden. Men det betyder att 180-v också kan ligga i första eller andra kvadranten. T x om v=50 så är 180-v=130 och om v=130 så är 180-v=50

Eftersom cos(v) har olika tecken i dom två kvadranterna  så blir det två svar, ett positivt och ett negativt(x1 resp x2). 

Blev det klarare?

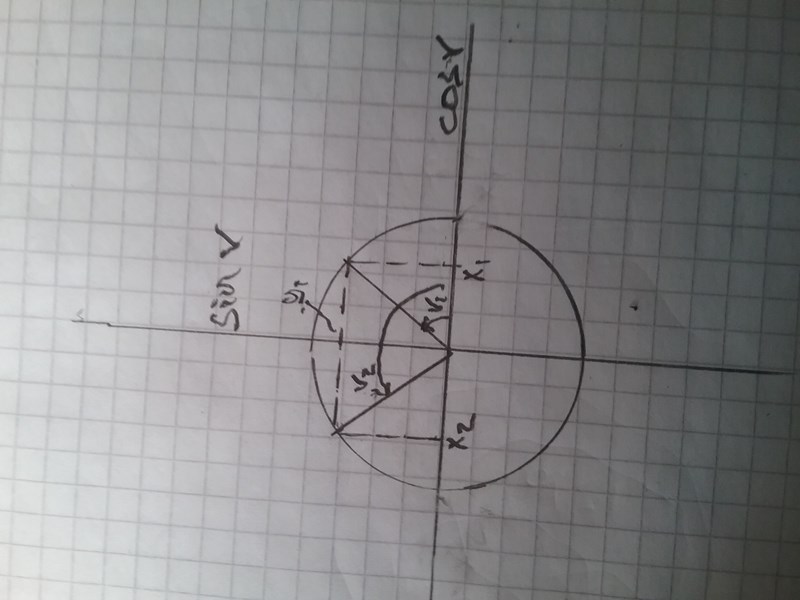
Tror att jag behöver ha en förklaring på det du skrev här ”Eftersom cos(v) har olika tecken i dom två kvadranterna  så blir det två svar, ett positivt och ett negativt(x1 resp x2). ”

Sin(v1) ochb sin(v2) läser du av på y-axeln har samma värde, =0,8 i det här fallet. Cos(v1) och cos(v2) läser du av på x-axeln, följ de streckade linjerna ner till x-axeln. Det blir -0,6 resp +0,6 i det här fallet.

Gäller det här hela tiden att man alltid ska kolla på de två vinklarna eller två värden som ger samma sinus eller cosinus värde?

Om du tittar på enhetscirkeln så kanske du kan förstå att det alltid blir två vinklar på varsin sida av x- resp ý-axeln som har samma cos- resp sin-värde. Tx om du har ett negativt cos-värde så är det en vinkel i andra och en vinkel i tredje kvadranten som har det cos-värdet.

Kan du ställa en kontroll fråga så att jag kan dubbel kolla att jag har förstått 100%?

Vad har sin för värde i fjärde kvadranten, positivt eller negativt? I vilken kvadrant finns det ett sin som har samma värde?

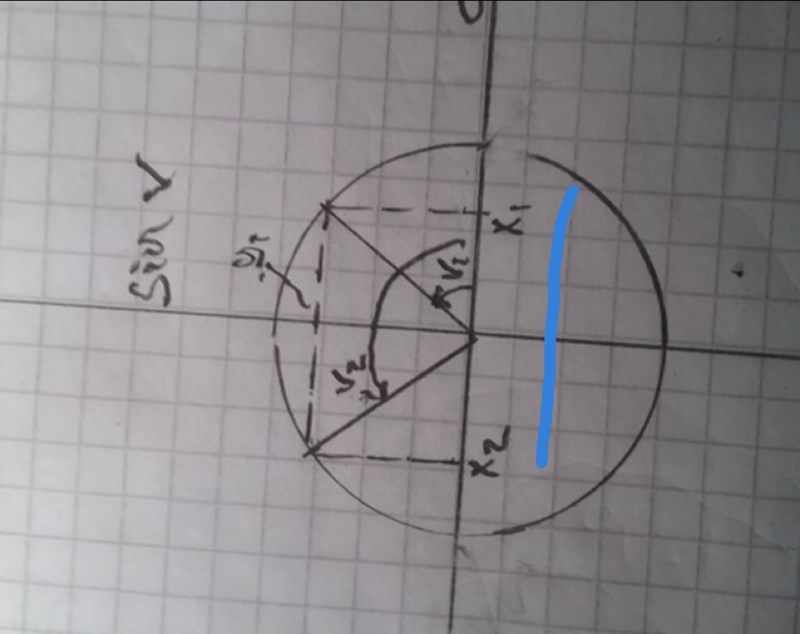Vet helt ärligt inte hur jag ska svara på din fråga. Men jag antar att det borde finnas både ett positivt och negativt värde. För varje sinus och cosinus har två värden

I fjärde kvadranten är du på y-axelns negativa sida, sin är alltså negativt. Även tredje kvadranten är på y-axelns negativa sida och där är alltså sin också negativt.

Tänk på att sin läser du av på y-axeln och cos på x-axeln,

Jag har ritat en vinkel i varje kvadrant, v1, v2, v3 och v4. Om jag har förstått det rätt så har du full koll på vilken kvadrant som är vilken men att du inte riktigt är med när jag anger hur man läser av respektive sin- och cos-värde. I figuren har jag angett var man läser av sin- och cos-värdena. Blev det bättre?

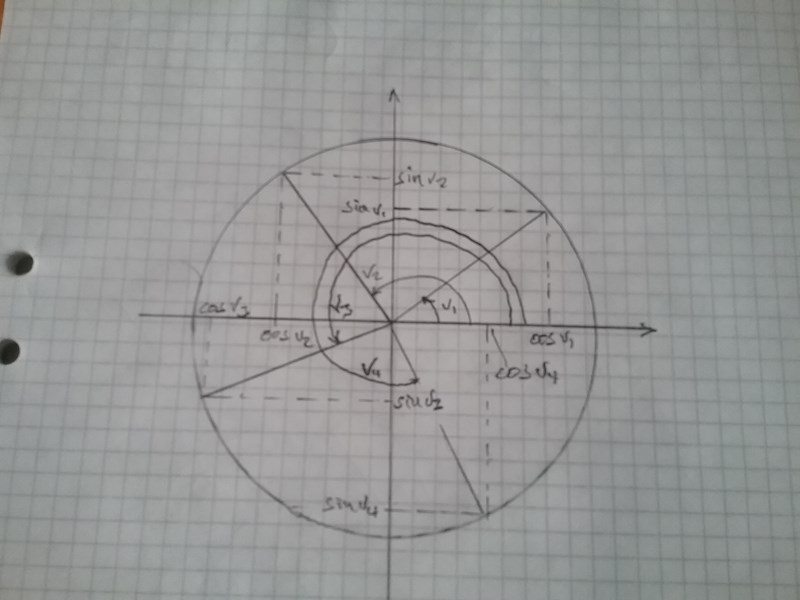
ostertalje skrev:

I fjärde kvadranten är du på y-axelns negativa sida, sin är alltså negativt. Även tredje kvadranten är på y-axelns negativa sida och där är alltså sin också negativt.

Tänk på att sin läser du av på y-axeln och cos på x-axeln,

Men du sa ju att det alltid kommer finnas två värden på cos och sin. Så varför är det endast ett negativt värde?

Sin(v3) och sin(v4) är båda negativa liksom att cos(v2) och cos(v3) är negativa. 

Har de inga positiva värden?

Tänk på att x är negativt från origo till vänster och y är negativt från origo och nedåt respektive positivt till höger och uppåt som Sten visade tidigare. Det är ett vanligt koordinatsystem. När det gäller 1:a och 2:a kvadranten så är x-värdet  positiv i första kvadranten men negativ i andra kvadranten. När det gäller 3:dje och 4:dje kvadranten så är x-värdet negativt i båda för de ligger båda till vänster om origo. Så det är inte alltid olika tecken på värdena. 

Okej. Alltså gäller det endast i första och andra kvadranten som det finns två olika värden på cosinus och sinus. Där den ena är positivt och det andra negativt. Medans i den tredje och fjärde kvadranten så finns det endast negativa värden på sin och cosinus. Skulle du kunna ge exempel på detta så att det blir lite tydligare

Om du har v = 30 så ligger v i första kvadraten då är cos v positiv. Om vi tar 180-v = 150 så ligger den i andra kvadraten och cos(180-v) = cos 150 är negativ men lika stort x-värde. Det har du sett. Sen har vi v= -30. Det ger samma x-värde och är positiv man säger att cos(-v) = cos (v)

Det här är x vi pratat om men samma gäller y fast då är det lite skillnad

Om vi har  v = 30 så är sin v positiv om vi tar sin 150 då är det också positivt för det ligger båda över origo där y är positiv. 

Jag fortsätter med cosinus

Sen har vi t ex cos (180 + v) = cos (180 + 30) = cos 210 för att bara ta ett exempel på en vinkel i tredje kvadranten den är negativ då den ligger till vänster om origo. Sen har den sin motsvarighet i fjärde kvadranten

210 -180 = 30 grader från 180 grader om vi går ned -30 grader från 0 grader så hittar vi motsvarigheten i fjärde kvadranten för 210 grader i tredje kvadranten . Så cos(-30 grader) är positiv för den ligger till höger om origo.

 
Ta och rita detta med ett koordinatsystem i mitten. Jag tror det är bra för att förstå vad som är negativt och positivt och vilka värden som hör ihop då de har samma x respektive y värden som ibland är negativa och ibland är positiva, beroende på var de ligger i koordinatsystemet, men x1 och x2 respektive y1 och y2 är alltid lika stora till beloppen.

Enhetscirkeln är mycket bra att förstå ordentligt då den underlättar väldigt mycket förståelsen för trigonometri.

Det känns att det är ganska mycket att få in. Och svårt för mig att hänga med på det du skriver. Vore bättre om du förklarade med bilder istället för text. Jag brukar ha lättare för att förstå bilder 

Sten har ritat så bra bilder. Kan du inte försöka själv? Läs min text och försök. Det bästa är att du försöker själv. Så försök genom att läsa min text långsamt. Rita ett koordinatsystem med pilar i x och y som vanligt. Skickar bara enenhetscirkel som inspiration. Här är 30 grader och 30+90 grader så det är olika x-värden.och en cirkel runt origo.