Räkna med centripetalkraft och allmäna gravitationslagen
Hej!
Jag har en förståelsefråga. I Heureka 2, kapitel 4 har jag stött på uppgifter av följande slag:
En satellit placeras i cirkelbana kring jorden med hjälp av en raket, som når höjden 1,0*103 km, där satelliten tilldelas en hastighet vinkelrät mot lodlinjen. Hur stor ska farten vara för att satellitens bana ska bli en cirkel?
Jag försökte såhär:
Jordens radius: 6,371*103 km + höjden 1,0*103 = 7,371*103 km.
v=?
v = 2*pi*r/T
v = 2*pi*7,371*103/24
v=1,9*103 km/h, vilket är fel.
I lösningen står det att man ska använda sig av formeln för centripetalkraften OCH den allmäna gravitationslagen;
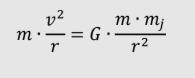
Min fråga är: VARFÖR? :D Varför kan man inte göra som ajag försökte?
Hoppas ni kan hjälpa mig! :)
Varifrån får du att periodtiden är (timmar?)? Jorden roterar visserligen runt sin egen axel med den ungefärliga omloppstiden , men det betyder inte att något i omloppsbana kring jorden också gör det! Exempelvis har den internationella rymdstationen en omloppstid på enbart !
Hastigheten bestäms ju snarare av det faktum att gravitationskraften som drar satelliten mot jorden ska vara lika med kraften som slungar satelliten bort från jorden, så att satelliten varken närmar sig jorden eller kommer längre i från den (på så sätt blir banan en cirkel).
Ahhh tack! Det du säger förklarar en del. :)
En fråga till:
"Hastigheten bestäms ju snarare av det faktum att gravitationskraften som drar satelliten mot jorden ska vara lika med kraften som slungar satelliten bort från jorden."
Vilken kraft är det som slungar satelliten bort från jorden? Centripetalkraften är väl också riktat in mot kretsens centrum (aka jordens mittpunkt) eller?
Om det inte hade funnits en kraft som fick satelliten att svänga i en cirkel runt Jorden, så skulle de ha fortsatt rakt fram med konstant hastighet.
Minka007 skrev:Vilken kraft är det som slungar satelliten bort från jorden? Centripetalkraften är väl också riktat in mot kretsens centrum (aka jordens mittpunkt) eller?
Kraften som gör det är den reaktiva centrifugalkraften
vilken är en kraft som är lika stor men motriktad centripetalkraften. Den yttre kraften är gravitationskraften och den måste vara lika stor som centrifugalkraften så att objektet stannar i sin bana.
Du kan läsa mer här:
@Ebola
Tack sååå mycket! Allting bara verkade suga in satelliten mot mitten. Nu vet jag bättre hur det funkar!
Minka007 skrev:@Ebola
Tack sååå mycket! Allting bara verkade suga in satelliten mot mitten. Nu vet jag bättre hur det funkar!
Satelliten faller hela tiden in mot mitten.
Ska man dra in en centrifugalkraft i resonemanget så får man komma ihåg att det inte är en riktig kraft.





