Räkna ut krafterna
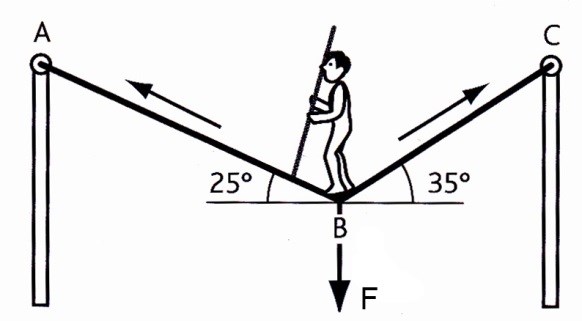
En lindansare med massan 55 kg balanserar på linan enligt figuren. Hur stora blir krafterna i lindelarna AB och BC?
Hur ska jag räkna ut detta? Kom gärna med tips!
Välkommen till Pluggakuten!
Det är extremt svårt att svara på det utan tillgång till din figur. Kan du ta en bild och ladda upp? För att ladda upp en bild använder du knappen näst längst till höger i inskrivningsrutan, den som ser ut som ett foto av ett berg och en sol.
Hej! har problem med samma uträkning! skulle verkligen uppskatta en förklaring på denna uppgift så jag förstår uträkningsmetoden
Dela upp krafterna i linorna i vågräta respektive lodräta komposanter. Kraften åt höger skall vara lika stor som kraften åt vänster. Summan av de båda krafterna uppåt skall vara lika stor som kraften neråt. Du har nytta av trigonometri i den här uppgiften.
Jag har samma uppgift men på min står de tips tänk x-led och y-led?? Vad menas och hur ska jag tänka?? Tack på förhand
Man brukar räkna x-led höger-vänster. Positiva krafter åt höger, negativa åt vänster.
Y-led är på samma sätt uppåt-neråt.
En (kanske?) kompletterande bild på det Bubo skrev: 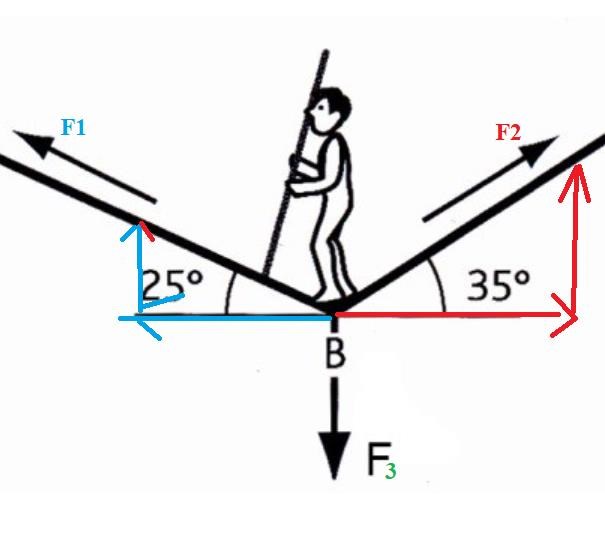 Edit: Namnsätt krafterna till något lämpligt och kör på med newton 2an i riktningarna x och y (där x är höger/vänster och y upp/ner) Tänk på riktningar och glöm inte kraften jag märkt som F3.
Edit: Namnsätt krafterna till något lämpligt och kör på med newton 2an i riktningarna x och y (där x är höger/vänster och y upp/ner) Tänk på riktningar och glöm inte kraften jag märkt som F3.
Tack så mycket för hjälpen men jag läser teknik 1 och är riktigt dålig på såna här uträkningar men skulle nån orkar göra en tydlig uträkning på hela den här så jag förstår hur jag ska tänka...alltså så en som inte kan sånt här lär sig de :)
x-led = 0:
y-led = mg
Tack så mycket affe jkpg
Nu får jag försöka förstå de här:)
Hur stora blir krafterna i AB och BC?
Gruvis skrev:Hur stora blir krafterna i AB och BC?
Visa hur du har försökt lösa uppgiften
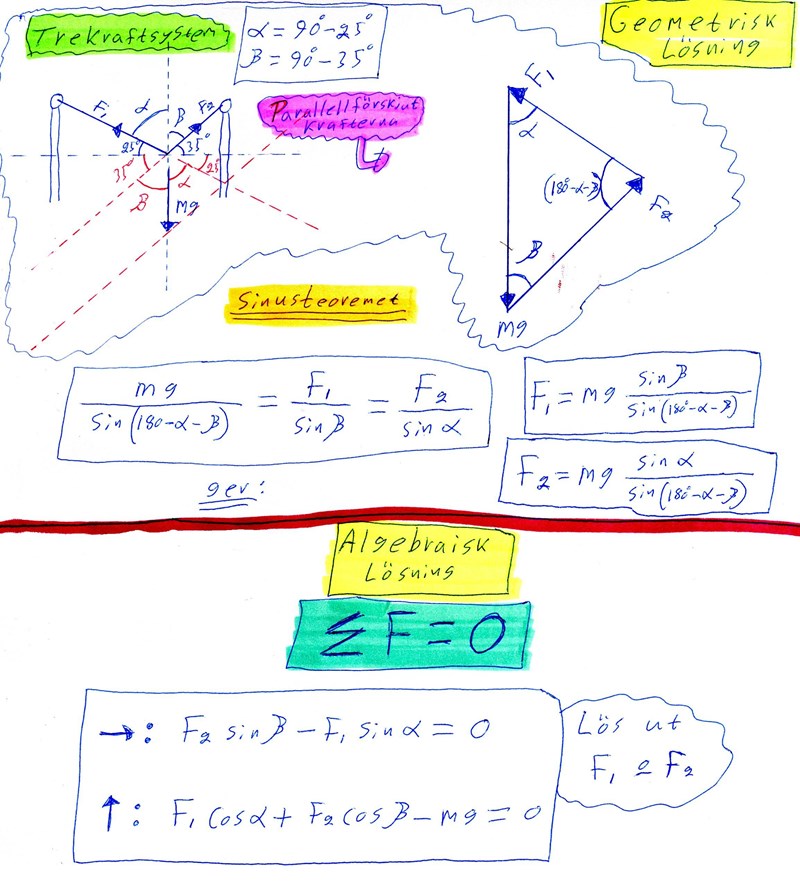
Affes formler kan man uttrycka så här i ord:
Den vågräta blå pilen och den vågräta röda pilen är lika stora, åt motsatta håll. (Summan av dem är noll)
Den lodräta blå pilen plus den lodräta röda pilen blir tillsammans lika mycket som tyngdkraften mg. (Summan av de tre krafterna blir noll)
Gruvis skrev:Hur stora blir krafterna i AB och BC?
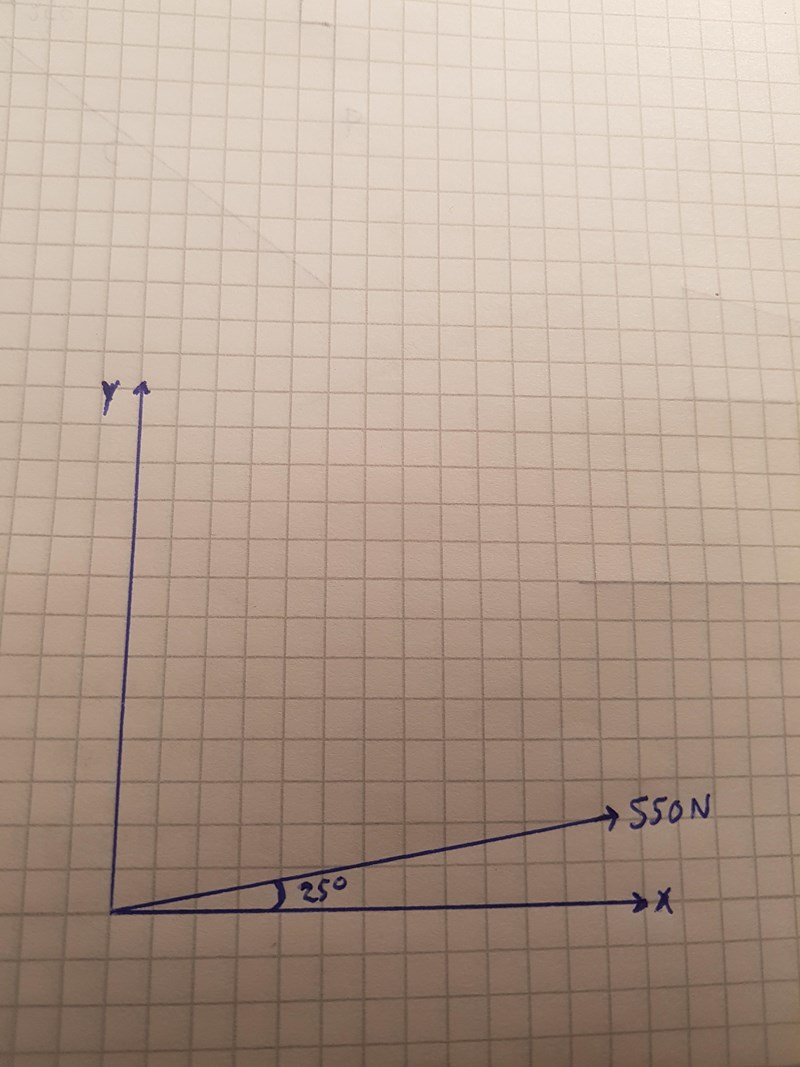
Men eftersom att jag aldrig gjort nått sånt här så har jag väldigt svårt att förstå hur jag ska tänka
Räknar man ut talen i Affes uppställning får man
F1 * 0,906 = F2 * 0,819
9.82*55 = F1 * 0,423 + F2 * 0,574
Har du löst sådana förut?
Laguna skrev:Räknar man ut talen i Affes uppställning får man
F1 * 0,906 = F2 * 0,819
9.82*55 = F1 * 0,423 + F2 * 0,574Har du löst sådana förut?
Du visar på någon slags meningsfull pedagogisk poäng.
Sedan brukar jag ändå nitiskt förespråka att man inte bör beräkna (till synes) meningslösa mellanresutat (cos(), sin()), utan hålla sig till bokstavs-ekvationer ända tills slutresultaten (här F1 och F2) ska beräknas.
Affe Jkpg skrev:Laguna skrev:Räknar man ut talen i Affes uppställning får man
F1 * 0,906 = F2 * 0,819
9.82*55 = F1 * 0,423 + F2 * 0,574Har du löst sådana förut?
Du visar på någon slags meningsfull pedagogisk poäng.
Sedan brukar jag ändå nitiskt förespråka att man inte bör beräkna (till synes) meningslösa mellanresutat (cos(), sin()), utan hålla sig till bokstavs-ekvationer ända tills slutresultaten (här F1 och F2) ska beräknas.
Jag hoppas den är meningsfull. Det kanske finns bättre ledtrådar. Jag ville se om det var ekvationslösandet som sådant som var hindret. Jag håller helt med dig annars.
För att möjligen göra ett ännu enklare exempel än vad Laguna skriver.
Har du löst något som liknar detta:
Tack så mycke för hjälpen....Jag har bara läst matte A på gymnasiet och de där med ekvationer var aldrig min grej men nu 15 år efter gymnasiet så ville jag läsa till teknik på komvux till mitt slutbetyg och så dök den här uppgiften upp och jag får inte in de i huvudet😊
Laguna skrev:Räknar man ut talen i Affes uppställning får man
F1 * 0,906 = F2 * 0,819
9.82*55 = F1 * 0,423 + F2 * 0,574Har du löst sådana förut?
Nä men jag lär mig gärna grunderna till att lösa såna:) De hade nog hjälpt enormt
Gruvis skrev:Laguna skrev:Räknar man ut talen i Affes uppställning får man
F1 * 0,906 = F2 * 0,819
9.82*55 = F1 * 0,423 + F2 * 0,574Har du löst sådana förut?
Nä men jag lär mig gärna grunderna till att lösa såna:) De hade nog hjälpt enormt
Ett litet exempel:
Gruvis skrev:Laguna skrev:Räknar man ut talen i Affes uppställning får man
F1 * 0,906 = F2 * 0,819
9.82*55 = F1 * 0,423 + F2 * 0,574Har du löst sådana förut?
Nä men jag lär mig gärna grunderna till att lösa såna:) De hade nog hjälpt enormt
Att lösa linjära ekvationssystem med 2 obekanta lär man sig i Ma2. Det finns tre olika metoder att lösa sådana - substitutionsmetoden, additionsmetoden och grafisk lösning.
Smaragdalena skrev:Gruvis skrev:Laguna skrev:Räknar man ut talen i Affes uppställning får man
F1 * 0,906 = F2 * 0,819
9.82*55 = F1 * 0,423 + F2 * 0,574Har du löst sådana förut?
Nä men jag lär mig gärna grunderna till att lösa såna:) De hade nog hjälpt enormt
Att lösa linjära ekvationssystem med 2 obekanta lär man sig i Ma2. Det finns tre olika metoder att lösa sådana - substitutionsmetoden, additionsmetoden och grafisk lösning.
Jag Gör just nu Teknik 1 på distan och har före detta inte pluggat på 10 r sedan jag hoppat av gymnasiet. Jag är nu på denna uppgift. Problemet med denna tråd som redan finns är att jag inte förstår alls vad som menas med alla olika F och bokstäver. Begriper inte alls dessa siffror och bokstäver och förstår för mitt liv inte vad som ska göras eller hur jag ska tänka. Uppgiften ska jag lämna in på onsdag och detta är mitt sista försök att få hjälp och hoppas att någon kan förklara lite mer ingående för en person som har lässvårigtheter. Mvh Erik
sprite111 skrev:En (kanske?) kompletterande bild på det Bubo skrev:
Edit: Namnsätt krafterna till något lämpligt och kör på med newton 2an i riktningarna x och y (där x är höger/vänster och y upp/ner) Tänk på riktningar och glöm inte kraften jag märkt som F3.
Hej HerrErik!
I figuren ovan illustreras tre krafter F1, F2 och F3
HerrErik, gör en ny tråd där du visar hur långt DU har kommit med problemet i stället för att väcka upp en gammal zombie-tråd. /moderator
HerrErik, om det är en inlämning bör du bara fråga om hjälp om din lärare uttryckligen har skrivit att detta är tillåtet. /moderator
EDIT: Välkommen hit när du har fler uppgifter du behöver hjälp med! Gör en tråd för varje fråga och lägg den i rätt forumdel, ge varje tråd en beskrivande rubrik och visa hur du har försökt och hur långt du har kommit, så kommer du förmodligen att få så mycket hjälp du behöver!
När jag editerade blev jag tvungen att flytta tråden till rätt nivå - chansade på gymnasienivå.