Räkna ut sidor på rätvinklig triangel utan trigonometri

Hej!

Jag fick nyligen denna fråga av min mattelärare då han inte kunde lösa den och ville ha hjälp. Jag har pratat med samtliga av mina vänner som går på universitet men än så länge har ingen löst uppgiften.

"När Ivan ska hälsa på sin mormor behöver han gå över ett berg som är 20 km brett och vars bergssidor är 30º och 45º mot plan mark (se bild). Hur mycket längre måste Ivan gå än om han bara kunde gå rakt igenom berget?"

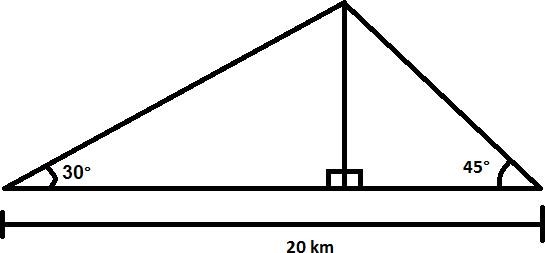
Vi bestämde att hypotenusan på den vänstra triangeln skulle kallas a och hypotenusan på den högra för b. Detta innebär att vi ska räkna ut hur mycket längre a+b är än 20.

Det vi än så länge har kommit fram till är att höjden är $\frac{a}{2}$ då det går att måla en kongruent triangel under den vänstra vilket skapar en liksidig triangel med sidorna a. Vi har även kommit fram till att den högra triangeln är likbent då även den övre vinkeln är 45º, vilket leder till att basen på den högra triangeln också är $\frac{a}{2}$ . Basen på den vänstra triangeln är $20 - \frac{a}{2}$ .

Detta ska lösas utan trigonometri och enligt bedömningshänvisningarna ska man ställa upp ett ekvationssystem för att räkna ut höjden eller de två baserna. Höjden ska även bli ca 7.32 om man ställt upp ekvationssystemet rätt och räknat ut allt korrekt.

Tacksam för all hjälp jag kan få!

Om man vet att triangeln med vinkel 30° är "en halv liksidig triangel" och att triangeln med vinkel 45° är "en halv kvadrat" så kan det lösas "utan trigonometri" med Pythagoras sats.

Det går bara när vi redan vet höjden på de båda trianglarna vilket vi inte gör. Den höjden jag skrev fick jag från bedömningshänvisningarna, men jag behöver vägen dit.

Fast förhållandena mellan sidor i halva liksidiga trianglar och halva kvadrater vet man "utan trigonometri".

Det har vi redan kommit fram till. Det är fortsättningen som är problemet

Med höjden h så är övriga sidor

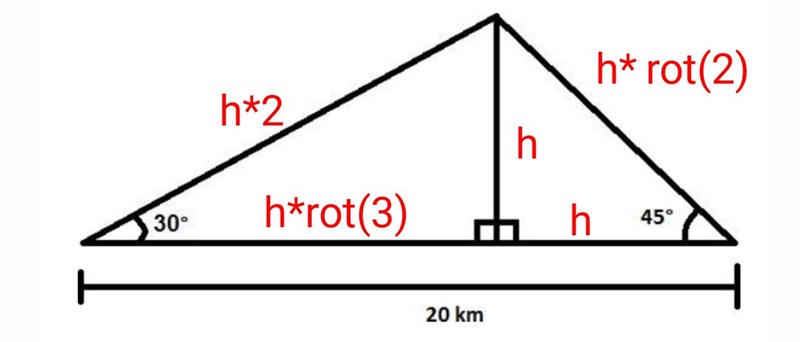
Det är det vi har kommit fram till, fast med a. Höjden är a/2 och den stora basen är 20-(a/2)

Om du kommit så långt så är du ju nästan klar. Med hänvisning till Dr G’s figur så kan du ställa upp ekvationen $h(\sqrt3+1)=20$ och lösa ut vad $h$ är.

Med dina beteckningar så får du ut a om du ställer upp Pythagoras sats för 30°-triangeln.

Dear värdena som Dr. G satte ut är på för hög nivå för matte 2c.

Jag försökte räkna ut a med Pythagoras sats, men det blev inte rätt svar.

jeffner skrev :
Dear värdena som Dr. G satte ut är på för hög nivå för matte 2c.

Nej det är de inte. De är alla baserade på Pythagoras sats.

Om vi säger att höjden är h så är även högra triangelns bas h (den är ju likbent), Alltså är hypotenusan lika med $\sqrt{h^{2} + h^{2}} = \sqrt{2 h^{2}} = h \sqrt{2}$ enligt Pythagoras sats.

Den högra triangeln är en halv liksidig triangel, vilket gör att hypotenusan är $2h$ och den långa kateten är lika med $\sqrt{(2 h)^{2} - h^{2}} = \sqrt{4 h^{2} - h^{2}} = \sqrt{3 h^{2}} = h \sqrt{3}$ enligt Pythagoras sats.

rot(2) betyder här alltså $\sqrt{2}$ och rot(3) betyder $\sqrt{3}$

Jag försökte räkna ut a med Pythagoras sats, men det blev inte rätt svar.

Hur räknade du och vad fick du för svar?

Jag räknade ut $a = \sqrt{(20 - \frac{a}{2})^{2} + (\frac{a}{2})^{2}}$ och fick fram att a≈13.178. Jag kan dock ha räknat fel någonstans utan att själv se det.

Med Dr.Gs figur är förhållandet mellan sträckorna $(2 h + h \sqrt{2}) / (h \sqrt{3} + h)$ = $(\sqrt{2} + 2) / (\sqrt{3} + 1) \approx 1, 25$ .

Så sträckan över berget är 5 km längre.

Edit: Och tråden 5 år gammal ser jag nu.

Svara Avbryt

Visa senaste svar