Räkna ut stödreaktioner på en balk med tre stöd
Hej!

Jag har försökt att lösa denna uppgift, men har haft svårt att veta exakt hur jag ska gå tillväga. Ett sätt att lösa denna uppgift är att använda sig av en metod ”Three moment equation”, men det är ingenting som låter bekant från universitetet och känns invecklat då man blandar in formler som inte finns med i mitt formelblad.
Ett annat sätt att lösa den här uppgiften på är att använda sig av superpositionsmetoden, tror jag. Man delar upp balken i olika delar och kollar upp elementarfall som man sedan adderar ihop för att lösa ut en reaktionskraft. Tänker jag rätt nu?
Superposition går säkert att använda. Jag vet inte vad "three moment equation" är, men det borde gå bra att använda grundbegreppen: ställa upp alla ekvationer som går med moment och kraftjämvikt.
Den där utbredda lasten borde man kunna behandla som en punktkraft i dess tyngdpunkt.
Laguna skrev:Superposition går säkert att använda. Jag vet inte vad "three moment equation" är, men det borde gå bra att använda grundbegreppen: ställa upp alla ekvationer som går med moment och kraftjämvikt.
Den där utbredda lasten borde man kunna behandla som en punktkraft i dess tyngdpunkt.
Jag följde ditt förslag och behandlade den utbreda lasten som en punktkraft i dess tyngdpunkt, ställde upp ekvationer för jämvikt och räknade på moment. Då fick jag fram dessa ekvationer
RA + RC + RD = 200
4RA - 5RD = -275
4RC + 9RD = 1075
Känns som att dessa ekvationer stämmer eftersom när jag sätter in de rätta värdena på RA, RC, och RD (Kollade upp reaktionskrafterna med hjälp av ett program), så stämmer det överens med ekvationerna. När jag läser ut de får jag dock andra värden där RD = 0?
Då har du gjort något fel. Teckenfel kanske.
Laguna skrev:Då har du gjort något fel. Teckenfel kanske.
Jag använde mig av gausselimination för matriser och fick att RA = -68.75, RC=268.75 och RD = 0. Dubellkollade med ett program på nätet som räknar ut matriser och fick fram dessa värden även där.
RA ska dock egentligen vara 7.81, RC ska vara 130.93, och RD 61,25. Dessa värden stämmer bra överens med ekvationerna, men det gör även de felaktiga värdena jag fick fram? Blir förvirrad 😕
Aha, de tre ekvationerna är inte oberoende, så det finns oändligt många lösningar. Om du adderar de två sista får du fyra gånger den första.
Du behöver nån mer ekvation.
Problemet är statiskt obestämt på grund av redundans; alltså fler stöd än statiskt nödvändigt. Detta leder till att du får ett ekvationssystem där lika många antal ekvationer som redundanser +1 är linjärt beroende av varandra, alltså två.
Detta är synonymt med att du behöver en till ekvation. Detta är oftast från kompatibilitet, linjärisering av deformationen (Antag små deformationer och formulera ett samband) eller superposition av lösningar för den elastiska linjens ekvation. Alltså, normalt superposition av Elementarfall. Det finns approximativa energimetoder också eller virtuella arbetets princip men dessa tar man normalt inte inom hållfasthetslära på kandidatnivå.
Victordobado skrev:Ett sätt att lösa denna uppgift är att använda sig av en metod ”Three moment equation”, men det är ingenting som låter bekant från universitetet och känns invecklat då man blandar in formler som inte finns med i mitt formelblad.
Naej, det går inte i detta fall. Det går bara för statiskt bestämda system. Kruxet i denna uppgift är att alla okända laster har parallella verkningslinjer. Det är ett typiskt problem för statiskt obestämda balksystem att "Three moment equation" inte fungerar. För ett statiskt bestämt system kan du välja vilka tre punkter som helst och formulera momentjämvikt kring och producera en entydig lösning. Detta känner du säkert igen från mekaniken.
Tillägg: 1 aug 2023 00:21
Detta blev lite fel. Jag förstod inte att man med Three Moment equation menade Clapeyrons ekvation. Den blir ganska krånglig i detta fall då du har olika långa balklängder. Då kan du lika gärna köra superposition.
Annars kan du lära dig distribuerad teknik enligt Cross:
https://en.m.wikipedia.org/wiki/Moment_distribution_method
Eller här för enklare genomgång:
http://hb.diva-portal.org/smash/record.jsf?pid=diva2%3A1311451&dswid=-1613
SaintVenant skrev:Victordobado skrev:Ett sätt att lösa denna uppgift är att använda sig av en metod ”Three moment equation”, men det är ingenting som låter bekant från universitetet och känns invecklat då man blandar in formler som inte finns med i mitt formelblad.
Naej, det går inte i detta fall. Det går bara för statiskt bestämda system. Kruxet i denna uppgift är att alla okända laster har parallella verkningslinjer. Det är ett typiskt problem för statiskt obestämda balksystem att "Three moment equation" inte fungerar. För ett statiskt bestämt system kan du välja vilka tre punkter som helst och formulera momentjämvikt kring och producera en entydig lösning. Detta känner du säkert igen från mekaniken.
Tillägg: 1 aug 2023 00:21
Detta blev lite fel. Jag förstod inte att man med Three Moment equation menade Clapeyrons ekvation. Den blir ganska krånglig i detta fall då du har olika långa balklängder. Då kan du lika gärna köra superposition.
Annars kan du lära dig distribuerad teknik enligt Cross:
https://en.m.wikipedia.org/wiki/Moment_distribution_method
Eller här för enklare genomgång:
http://hb.diva-portal.org/smash/record.jsf?pid=diva2%3A1311451&dswid=-1613
Att räkna på superposition är tyvärr inte min starkaste sida. Läraren har bara nämnt teorin men inte gått igenom exempel och uträkningar. Fastnar på att förstå formlerna man ska använda sig av i formelbladet. Antar att man ska dela upp balken i olika delar och addera formler för olika elementarfall för nedböjningar för att sedan lösa ut en reaktionskraft? Kollade på den här videon och försökte göra något liknande, men det gick långt ifrån bra då jag var osäker på om jag ens använde rätt formler.
https://www.youtube.com/watch?v=KjLxoN6nAuI
I grunden handlar det om att utnyttja egenskapen hos linjära differentialekvationer som gör att en summa av lösningar också är en lösning.
Detta betyder att du kan räkna ut nedböjningen i punkt C för en fritt upplagd balk utan något stöd där men med lasterna på 50 k/N och 30 kN/m. Sedan räknar du för samma balk men nu lägger du till en reaktionskraft i C som pekar rakt upp och får utböjningen .
Eftersom du har ett stöd i punkt C innebär detta att:
Det som krånglar till det i detta fall är att du behöver Dirac delta och Heaviside step för att hantera dessa två laster samtidigt. Utan de matematiska redskapen måste du göra två olika uträkningar för båda olika fallen ovan. Detta blir fyra olika användningar av Elementarfall. Men, jämfört med Clapeyron, vinkeländringsmetod etc. tycker jag det är enklast.
Men, visa lite hur du försökt så ska du nog kunna få hjälp. Har du frågor om Elementarfall osv. kan du ställa dem också.
Tillägg: 2 aug 2023 00:25
Jag kan ge dig lite hjälp på traven och hänvisa till Macaulays metod då den är den absolut enklaste beskrivningen. Detta är en bra genomgång:
https://www.colincaprani.com/files/notes/SAIII/Macaulay%2527s%2520Method%25201011.pdf
Av någon anledning föredrar man snittning och superposition i Sverige men om du lär dig Macaulays metod kommer du kunna lösa alla problem mycket enklare, och snabbare.
Mitt tips är att du försöker läsa pdf:n ovan, den har många bra exempel och är pedagogisk. Den har sedan flera exempel som liknar ditt problem. Annars, om du verkligen inte vill lära dig något nytt inför omtenta eller vad det är, kan du lösa problemet med ren snittning och beskrivning av tre olika intervall med . Sedan integrerar du alla tre enskilt och ansätter randvillkor. Detta kommer producera den tredje ekvationen som du behöver. Kom ihåg att elastiska linjens ekvation ger:
SaintVenant skrev:I grunden handlar det om att utnyttja egenskapen hos linjära differentialekvationer som gör att en summa av lösningar också är en lösning.
Detta betyder att du kan räkna ut nedböjningen i punkt C för en fritt upplagd balk utan något stöd där men med lasterna på 50 k/N och 30 kN/m. Sedan räknar du för samma balk men nu lägger du till en reaktionskraft i C som pekar rakt upp och får utböjningen .
Eftersom du har ett stöd i punkt C innebär detta att:
Det som krånglar till det i detta fall är att du behöver Dirac delta och Heaviside step för att hantera dessa två laster samtidigt. Utan de matematiska redskapen måste du göra två olika uträkningar för båda olika fallen ovan. Detta blir fyra olika användningar av Elementarfall. Men, jämfört med Clapeyron, vinkeländringsmetod etc. tycker jag det är enklast.
Men, visa lite hur du försökt så ska du nog kunna få hjälp. Har du frågor om Elementarfall osv. kan du ställa dem också.
Tillägg: 2 aug 2023 00:25
Jag kan ge dig lite hjälp på traven och hänvisa till Macaulays metod då den är den absolut enklaste beskrivningen. Detta är en bra genomgång:
https://www.colincaprani.com/files/notes/SAIII/Macaulay%2527s%2520Method%25201011.pdf
Av någon anledning föredrar man snittning och superposition i Sverige men om du lär dig Macaulays metod kommer du kunna lösa alla problem mycket enklare, och snabbare.
Mitt tips är att du försöker läsa pdf:n ovan, den har många bra exempel och är pedagogisk. Den har sedan flera exempel som liknar ditt problem. Annars, om du verkligen inte vill lära dig något nytt inför omtenta eller vad det är, kan du lösa problemet med ren snittning och beskrivning av tre olika intervall med . Sedan integrerar du alla tre enskilt och ansätter randvillkor. Detta kommer producera den tredje ekvationen som du behöver. Kom ihåg att elastiska linjens ekvation ger:
Att kunna lösa det enkelt och snabbt med den där metoden hade varit schysst, men tyvärr kan jag inte öppna upp pdf:n. Får bara upp "Error 404 - Page not found!"
Ok! Jag ska försöka lösa det som du säger med randvillkor och elastiska linjens ekvation och se hur det går
Du måste trycka på "Desktop" om du sitter på mobilen på Colins hemsida. Annars kan du bara googla på Macaulays method Colin så kommer den upp som första alternativ:
https://www.google.com/search?q=macaulay+method+colin
Det är det bästa sättet att göra på och går väldigt snabbt. Snittning tror jag kommer bli en gröt av algebra som man helst inte vill göra för hand. Jag lägger upp en lösning med diskontinuitetsfunktioner enligt Macaulay under veckan när jag hinner.
SaintVenant skrev:Du måste trycka på "Desktop" om du sitter på mobilen på Colins hemsida. Annars kan du bara googla på Macaulays method Colin så kommer den upp som första alternativ:
https://www.google.com/search?q=macaulay+method+colin
Det är det bästa sättet att göra på och går väldigt snabbt. Snittning tror jag kommer bli en gröt av algebra som man helst inte vill göra för hand. Jag lägger upp en lösning med diskontinuitetsfunktioner enligt Macaulay under veckan när jag hinner.
Tack för länken! Jag ska läsa igenom den och se om det låter vettigt och förståeligt. Det är även otroligt snällt av dig att ta din tid och lägga upp ett lösningsförslag. Har kollat igenom vissa uträkningar gällande snittningen och det är ju väldigt mycket algebra och härledningar som gör en lite förvirrad
Detta är en friläggning av vår balk:

Vi har tre okända reaktionskrafter men bara två tillgängliga ekvationer. Detta avslöjar att strukturen har redundans och att problemet är statiskt obestämt.
Kraftjämvikt i vertikal led ger:
Moment kring punkt D ger:
Vi behöver nu en tredje ekvation för att lösa problemet. Denna kan vi från kompatibilitet och krav på strukturens deformationer. Jag kommer diskutera tre olika sätt:
- Elastiska linjens ekvation och snittning
- Superposition
- Macaulays metod
Elastiska linjens ekvation och snittning
Enligt elastiska linjens ekvation har vi följande differentialekvation:
Om vi snittar balken får vi tre olika intervall för från tre olika snitt.
Intervall
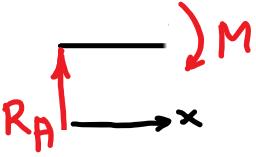
Vi får:
Intervall
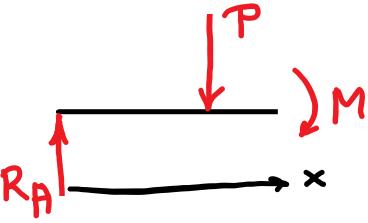
Vi får:
Intervall
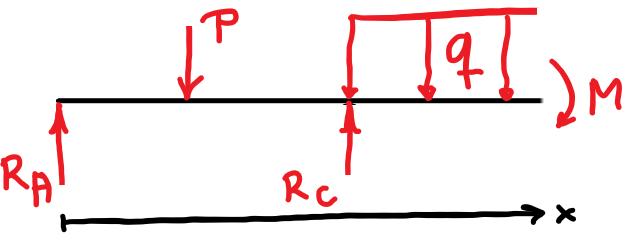
Vi får:
Dessa tre olika ekvationer ska nu alla enskilt integreras två gånger vilket kommer producera totalt 6 st integrationskonstanter vilka måste bestämmas med hjälp av randvillkor för de intervall där de är giltiga. Vi börjar med .
Första intervallet ()
Vi har två randvillkor att använda oss av och det är:
Andra intervallet ()
Randvillkor:
Tredje intervallet ()
Randvillkor:
Vi ser genast att detta är grötigt. Det finns sätt att effektivisera det på och några mindre förenklingar men i stort är det tidskrävande.
Superposition av elementarfall
Vi kan ersätta något av stöden A, C, eller D med en kraft och formulera vårt ursprungliga problem som summan av problem. Jag väljer stödet vid C och får:
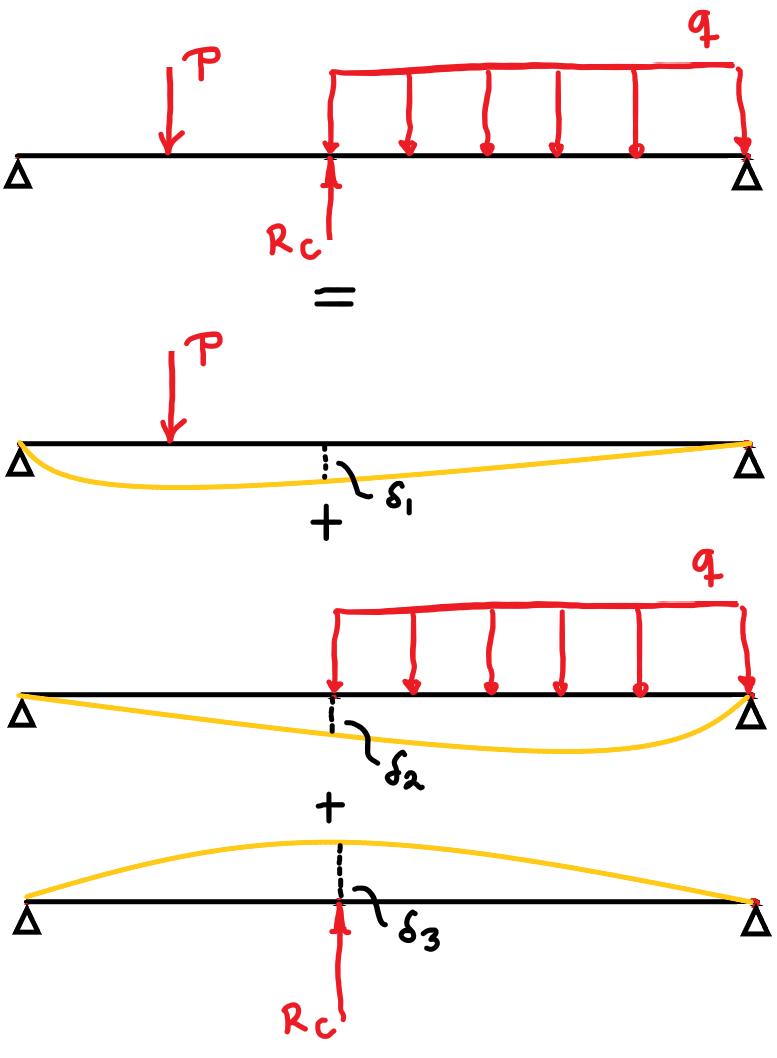
Dessa nedböjningar kan vi oftast få från elementarfall. Vi kommer då få den tredje ekvationen vi vill ha från kravet att:
Ett litet problem kan vara att fallet med enbart den utbredda lasten på en bit av balken oftast inte finns som elementarfall men då kan vi snitta och lösa. Vi får i alla fall om vi tittar i Handbok och formelsamling i Hållfasthetslära tabell 32.2 att:
Macaulays metod
Denna påminner om snittning med skillnaden att vi får fram en endaste ekvation för hela balken som vi hanterar i ett endaste snäpp med tungan rätt i mun. Vi använder oss av Macaulays funktioner som definieras enligt:
Vi får då fram:
Vi bestämmer integrationskonstanterna med randvillkor:
Sedan använder vi för att få den tredje ekvationen vi ville ha från början.
Vi kan antingen se det direkt eller veta sedan innan att randvillkoret kommer alltid tvinga andra integrationskonstanten till noll. Alltså, vi har:
Vi använder sedan randvillkoret och får:
Nu använder vi och får:
Detta förenklas till:
Vilket är vår sökta tredje ekvation. Tillsammans med de två första vi tog fram får vi:
Man kan kontrollera detta på flera sätt men enklast är med en egen numerisk balklösare eller någon online så som skyciv (länk).
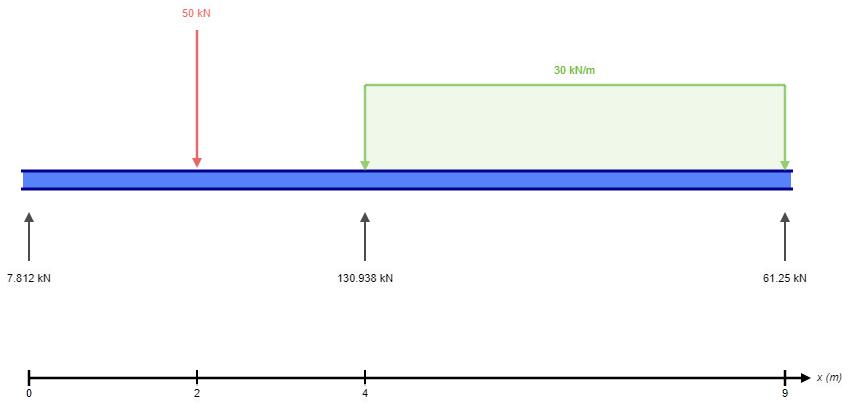
Resultatet är:
SaintVenant skrev:Vi kan antingen se det direkt eller veta sedan innan att randvillkoret kommer alltid tvinga andra integrationskonstanten till noll. Alltså, vi har:
Vi använder sedan randvillkoret och får:
Nu använder vi och får:
Detta förenklas till:
Vilket är vår sökta tredje ekvation. Tillsammans med de två första vi tog fram får vi:
Man kan kontrollera detta på flera sätt men enklast är med en egen numerisk balklösare eller någon online så som skyciv (länk).
Resultatet är:
Ett jättestort tack för att du tog din tid att lösa och förenkla detta. Känns som att vissa saker blev tydligare för mig nu. Tack!!!




