Hasse’s algorithm (räknelek)
Hej!
Jag undersöker det här problemet:
Utgå från ett valfritt positivt heltal n. Om n är jämnt, dividera det med två. Om det är udda, multiplicera det med tre, addera därefter ett, och dividera med 2. Upprepa detta till du når talet 1. Därefter så kommer cykeln [1,2] att bildas, och denna kallas för "the trivial cycle".
Än så länge har ingen lyckats bevisa att detta gäller för alla tal så problemet är olöst.
När jag läser om problemet står det såhär:
" The trivial cycle [1,2] is the only cycle of the function on the positive integers having period length less than 10,439,860,591. It is also the only cycle containing less than 6,586,818,670 odd integers"
När de skriver " ... is the only cycle of the function on the positive integers having period length less than 10,439,860,591." menar de då att det finns andra cykler ? (Fast då borde ju problemet vara löst om det hittat en annan cykel som inte inkluderar siffran 1?)
Vad menas med "having period length less than 10,439,860,591"?
Sedan står det såhär:
"A partial result on the conjecture is showing the minimal size of any non-trivial cycle is the 1993 paper of Shalom Eliahou which establishes any non trivial cycle has length at least 17,087,915. "
Vad menas med en "non-trivial cycle"? Är det trajektorian av ett tal som aldrig når 1?
Väldigt tacksam för svar!
Mvh KriAno
This tasks trivial cycle: 1, 2, 1, 2, 1, 2...…
Non-trivial cycle example (utan samband till uppgiften): 18, 29, 50, 1, 28, 5, 1878, ….
Eftersom engelskan tycks "halta", undrar jag över om man kan få läsa originaltexten....ällä ä dä Hasses svengelska?
Affe Jkpg skrev:This tasks trivial cycle: 1, 2, 1, 2, 1, 2...…
Non-trivial cycle example (utan samband till uppgiften): 18, 29, 50, 1, 28, 5, 1878, ….
Eftersom engelskan tycks "halta", undrar jag över om man kan få läsa originaltexten....ällä ä dä Hasses svengelska?
Hasse's algorithm är även känt som 3x+1 problemet.
Det första stycket:
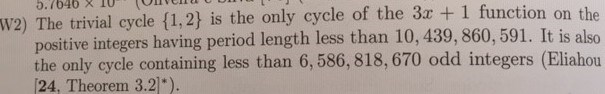
Det andra läste jag på den här sidan:
De menar att om det finns någon annan cykel (vilket inte är bevisat om det finns eller inte finns) så måste den ha en period längre än 10,439,860,591. En icke-trivial cykel är en trajektoria som är periodisk och inte är den triviala cykeln 1,2,1,2,... och det innebär alltså att den cykeln inte kan nå 1. Ett annat sätt att aldrig nå 1 skulle kunna vara en trajektoria som inte är begränsad (men det är inte heller bevisat om det finns eller inte finns, men probabilistiska argument finns för (heuristiskt) att det är osannolikt att en obegränsad trajektoria skulle finnas, men det är inget bevis).
dioid skrev:Ett annat sätt att aldrig nå 1 skulle kunna vara en trajektoria som inte är begränsad (men det är inte heller bevisat om det finns eller inte finns, men probabilistiska argument finns för (heuristiskt) att det är osannolikt att en obegränsad trajektoria skulle finnas, men det är inget bevis).
Ok, tack så mycket!
Men visst är en obegränsad trajektoria samma sak som en "divergent trajectory"?
Ja, det stämmer.
Om du missat det, senaste nytt ang Collatz conjecture (Hasse's algoritm):
https://www.quantamagazine.org/mathematician-terence-tao-and-the-collatz-conjecture-20191211/



