Räkning med Thales Sats
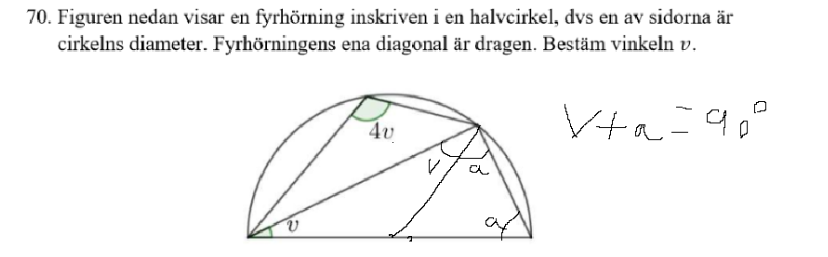
Har ingen aning vad jag ska göra efter det här. Svaret blir att v=30 grader, men vet inte hur jag ska komma fram till det. Dessutom vet jag inte hur jag kan använda 4v med i min uträkning..
Vinkeln 4v är en randvinkel
Kan du se motsvarande medelpunktsvinkel?
Vad säger randvinkelsatsen om dess storlek?
Kalla medelpunkten M och sätt ut
beteckningar på fyrhörningens hörn så blir det lättare att diskutera
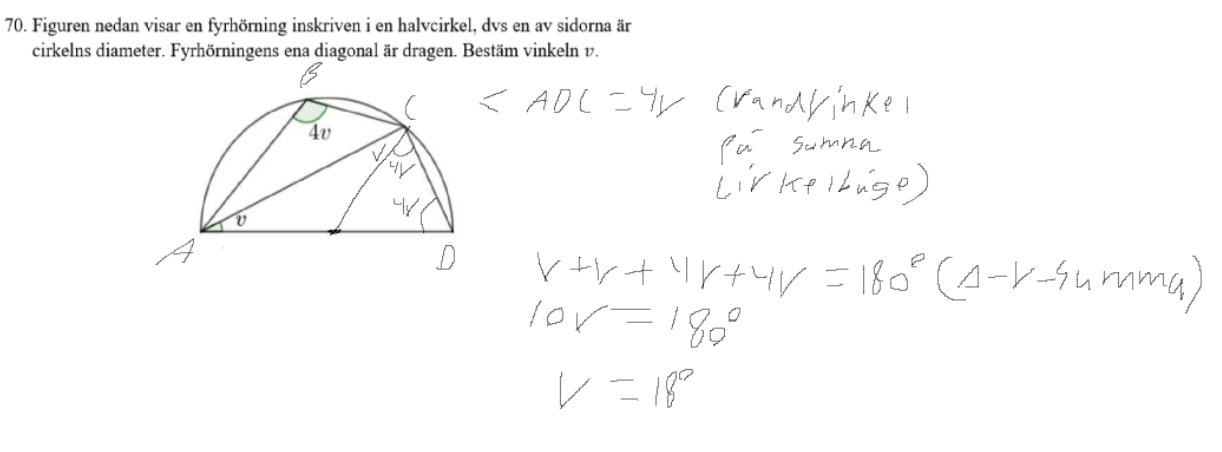
Nu tänkte jag att vinkel ADC är 4v eftersom den är en randvinkel på samma cirkelbåge som vinkel ABC. Dessutom konstaterade jag att vinkel CAD är samma som en av vinklarna vid ACD, nämligen den som bara är "v" eftersom de är basvinklar på grund av att det är en likbent triangel. Då får jag att 10v ska bli 180 grader, men då får jag 18 och inte 30. Det kan vara så att vinkeln jag satte som 4v egentligen är 2v, men jag ser inte det som en klassisk randvinkel där ena vinkeln är dubbelt så stor som den andra eftersom det inte finns någon klar mittpunkt utan bara faktumet att de delar samma cirkelbåge?
Vinkel ABC är randvinkel på den röda bågen.
Vinkel ADC är randvinkel på den blå bågen.
En randvinkel "gapar" mot sin båge.
Använd Arktos tips: vilken vinkel är medelpunktsvinkel på den röda bågen?
En annan infallsvinkel:
Vi återgår till din första figur, där du visat att v + a = 90° enl Thales sats
(som är ett specialfall av randvinkelsatsen när medelpunktsvinkeln är 180° ).
Nu kan vi använda oss av en annan sats i detta sammanhang, den som säger
att summan av motstående vinklar i en fyrhörning, som är inskriven i en cirkel,
är lika med 180°.
Här är därför [vinkel ABC] + [vinkel ADC] = 180°, dvs 4v + a = 180°
Vi vet redan att v + a = 90° .
Nu kan vi beräkna v .
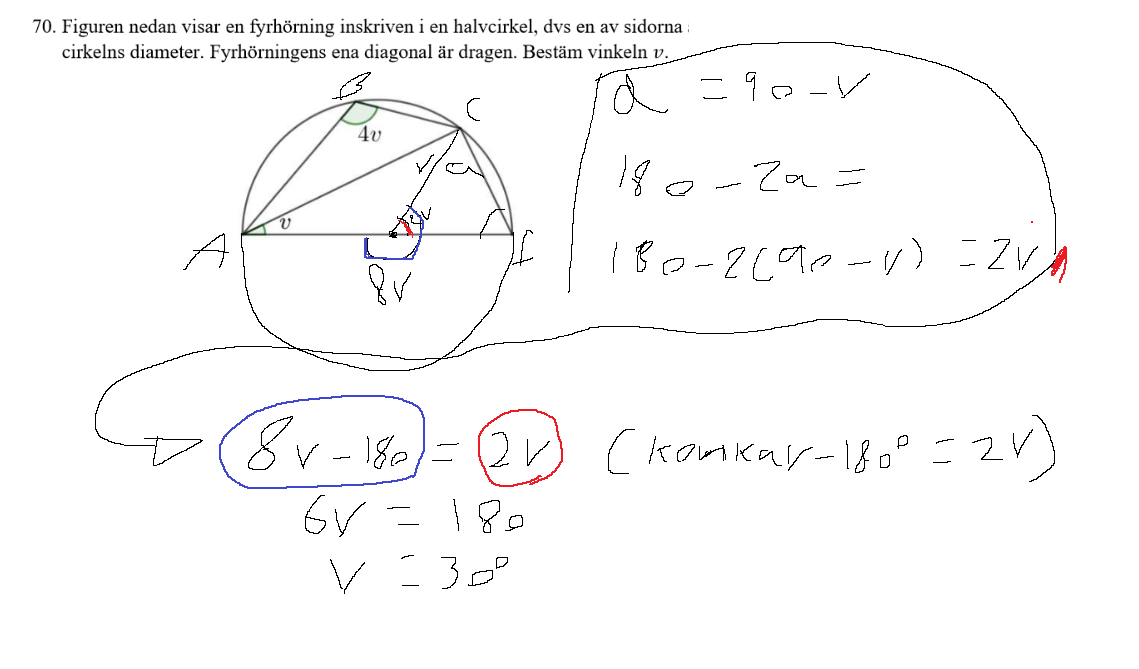Satsen du nämnde om en fyrkant inskriven i en cirkel gäller bara om den är inskriven i en hel cirkel, eller i en valfri del av en cirkel om två vinklar garanterat är 90 grader. I detta fallet har inte fyrkanten två räta vinklar i halvcirkeln så den satsen gäller inte, även om svaret för det blev rätt antar jag att det var av ren slump. Men oavsett lyckades jag lösa den. Randvinkeln 4v har en medelpunktsvinkel som är 8v. Dessutom så vet jag att vinkeln som är rödmarkerad är 2v. Om jag då bara tar 8v-180 får jag den vinkeln som är rödmarkerad, den som är 2v. Därefter gör jag en enkel ekvation och får att v=30 grader.
Tack för hjälpen.
Satsen du nämnde om en fyrkant inskriven i en cirkel gäller bara om den är inskriven i en hel cirkel, eller i en valfri del av en cirkel om två vinklar garanterat är 90 grader.
Jag blir nyfiken på var du hittade det påståendet. Som inte stämmer.
Montan skrev:
Satsen du nämnde om en fyrkant inskriven i en cirkel gäller bara om den är inskriven i en hel cirkel, eller i en valfri del av en cirkel om två vinklar garanterat är 90 grader. I detta fallet har inte fyrkanten två räta vinklar i halvcirkeln så den satsen gäller inte, även om svaret för det blev rätt antar jag att det var av ren slump. Men oavsett lyckades jag lösa den. Randvinkeln 4v har en medelpunktsvinkel som är 8v. Dessutom så vet jag att resonemanget i vinkeln som är rödmarkerad är 2v. Om jag då bara tar 8v-180 får jag den vinkeln som är rödmarkerad, den som är 2v. Därefter gör jag en enkel ekvation och får att v=30 grader.
Tack för hjälpen.
Också en bra lösning!
Men nog ligger alla fyrhörningens hörn på cirkeln, även om inget av dem ligger på den undre halvcirkeln? Se din figur i #6 . Så det är ingen tillfällighet att resonemanget i #5 ger en korrekt lösning.
Bra att du hittade den stora medelpunktsvinkeln 8v .
Mitt eget första lösningsförslag var att kombinera den med [vinkel AMC] till ekvationen (180 – 2v) + 8v = 360 som också fungerar.
Kul att se flera resonemang som leder till rätt lösning!
