Randvinkelsatsen

Det var en otydlig uppgift! Ser det inte ut som att den vinkel du ringat in är 150?

I så fall är 150 hälften av 360-α, enligt randvinkelsatsen. Alltså: 150=(360-α)/2. 

Jag blir förvirrad när randvinkelsatsen gäller för skulle den gälla kan man bara göra 360-150 viket är 210 sen  210/2 är 105 alltså a men det kan inte stämma när kan ja använda mig av denna metod 

Tror denna uppgiften så gäller det 150+a=180 alltså a ska vara 30

Fatima0277 skrev:

Tror denna uppgiften så gäller det 150+a=180 alltså a ska vara 30

Nej, det finns ingen anledning till att 150+α skulle vara =180. I så fall skulle övriga två vinklar i fyrhörningen vara 90 grader var och de är helt klart inte räta.

Tänk så här istället:

Randvinkelsatsen säger att randvinkeln som utgår från cirkelns rand (diameter) är hälften så stor som den som utgår ifrån centrum. Jag har kallat randvinkeln för β (=150) och centrumvinkeln för γ.

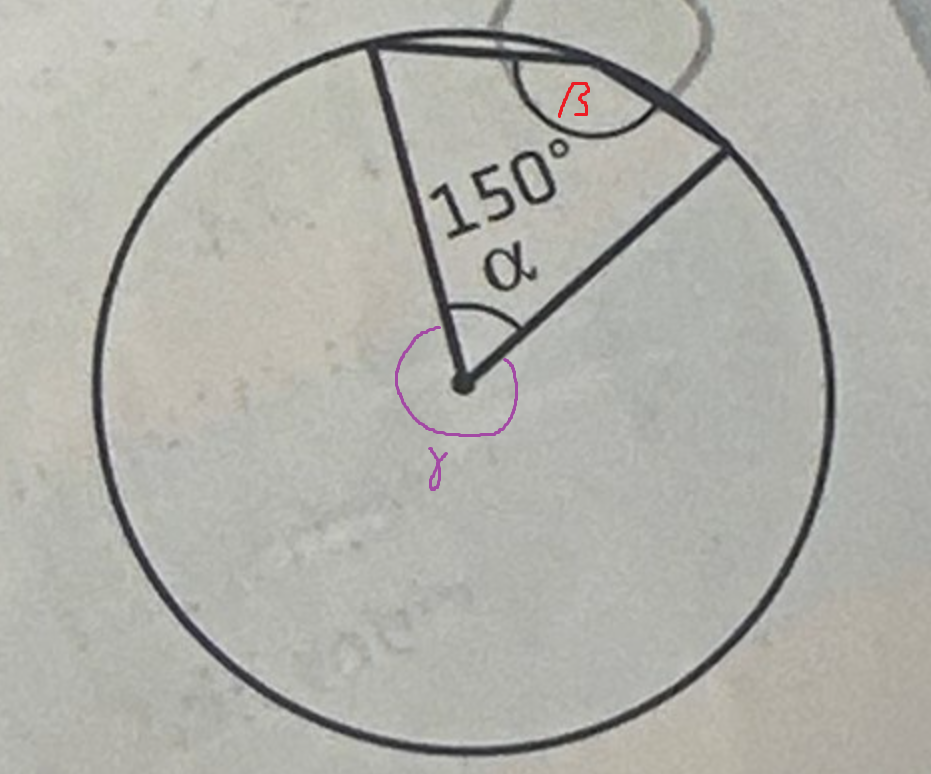
Randvinkelsatsen ger oss då β=γ/2.

Vi vet att β=150 samt att γ=360-α, så vi skriver 150=(360-α)/2.

Löser vi för α får vi: a=60.

Det som kanske är lite förvirrande är att gamma är >180 grader.

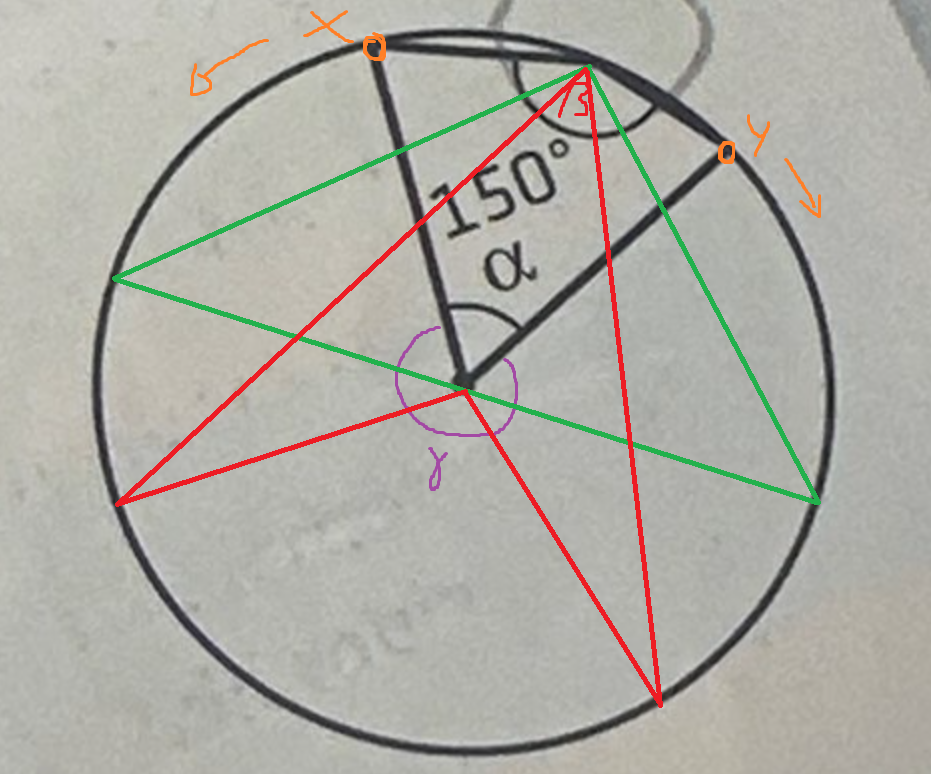
Tänk dig att du flyttar punkterna jag markerat som x och y i pilarnas riktning. Då kommer både γ och β att minska. 

Efter ett tag kommer vi till det gröna läget då vinklarna är 180 resp. 90. Sedan vidare mot det röda. Då kanske randvinkelsatsen är lättare att känna igen?

Förstår! 

Ett annat tips på hur man lättare kan se vilka medelpunkts-/randvinklar som hänger ihop med varandra är att man tydligt markerar den del av cirkelns rand som är motstående medelpunkts-/randvinkeln.

Om man gör så här så är det förhoppningsvis tydligt att randvinkeln som är 150° hänger ihop med medelpunktsvinkeln v: