RC kretsar

Hej! Bra, börja med att försöka tolka kretsen, utan att räkna på den. Du har redan insett att den högra delen av filtret är ett passivt högpassfilter. 

Den vänstra delen är ett aktivt filter, och det enklaste brukar vara att försöka jämföra med någon av de vanligaste op-kopplingarna.

Jag skulle identifiera op-kopplingen som en vanlig icke-inverterande förstärkare _om_ C1 kortsluts. Hur tecknas förstärkningen för en icke-inverterande förstärkare? Och hur påverkas den icke-inverterande förstärkningen om man kopplar tillbaka C1?

Kommer du vidare?

R1, tillsammans med  R2 och C1 bildar en icke konverterande OP amp, jag fattar också att R1 tillsammans med C1 bildar ytterligare högpassfilter - men hur tänker man vidare därifrån? Jag fattar inte hur jag ska få fram själva Av uttrycket? Jag brukar tänka Uut/Uin och tex få fram någon av de via nodanalys eller liknande och sen dela på varandra, men jag fattar inte hur man ska tänka på denna krets.... för vi har ett uttryck för den icke inverterande delen av kopplingen, och båda högpassfiltrerna - ska man då bara ta A1 x A2 x A3 och sen förenkla därifrån?

Ja, du kaskadkopplar de två filterstegen, multiplicerar överföringsfunktionerna med varandra. (Det är två filtersteg, ett aktivt och ett passivt). Eftersom

A1*A2 = Uut1/Uin1 * Uut2/Uin2 = {Uut1 = Uin2 eftersom kaskadkoppling} = Uin2/Uin1 * Uut2/Uin2 = Uut2/Uin1

Men du kan lika gärna få fram överförings- funktionen på hela filtret genom att räkna ut spänningar och strömmar. Det blir precis samma sak.

Vad är det som gör att du tycker det är svårt att beräkna Uut/Uin på just denna krets? Brukar du använda jw-metoden? 

Förstår du den här uppställningen, är det såhär du brukar göra?

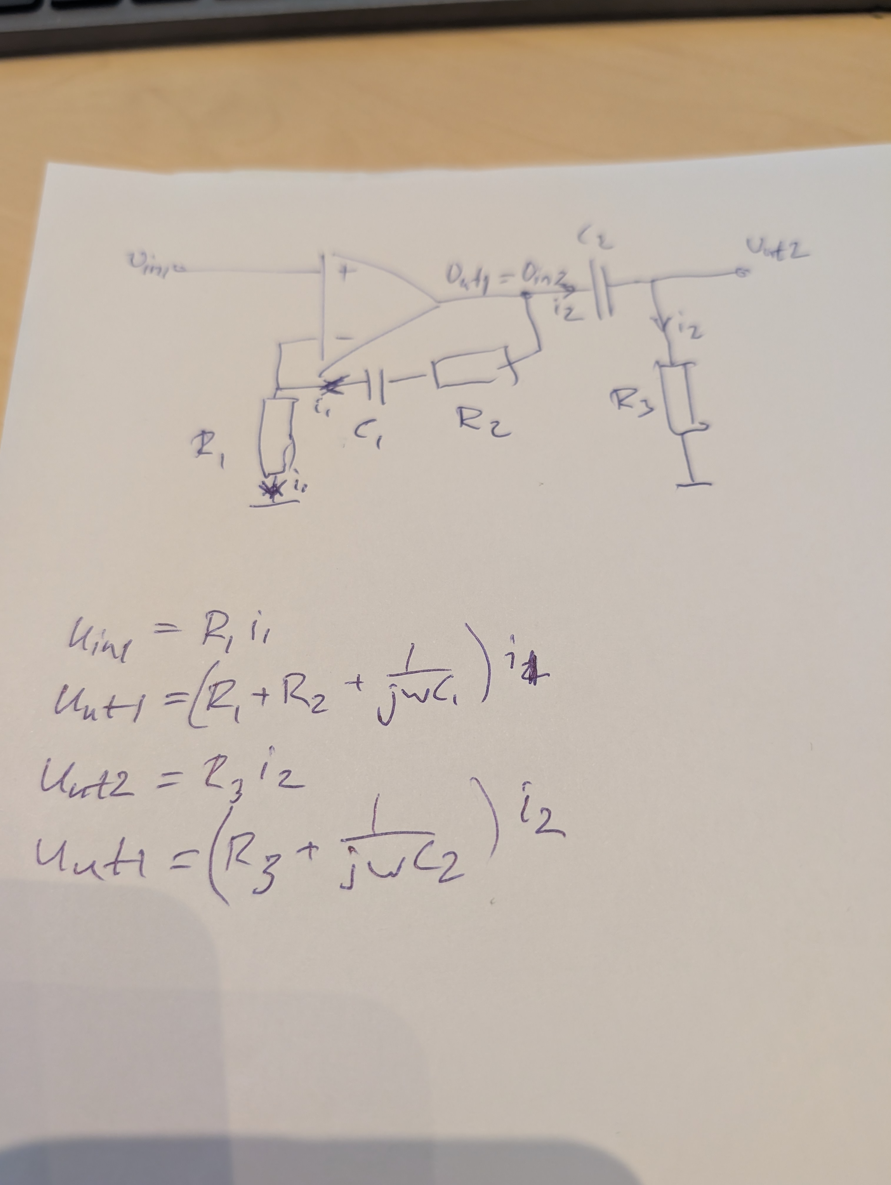
Ja, jag brukar göra så! Det jag tycker är svårt är hur allt liksom är kopplat. Jag tycker det oftast är svårt att se vad som är låg/högpass filter, samt hur man liksom använder det i beräkning (förutom när vi tex räknar brytfrekvenser). Jag har inte riktigt greppat just denna typ av uppgift. Jag tycker också förenklingen av jw-uttrycket till bodes normalform är tuff. Men jag tror jag börjar fatta nu! 

Kan du tänka såhär (den icke-inverterande förstärkaren är bara ett exempel, det andra konfigurationer också.)

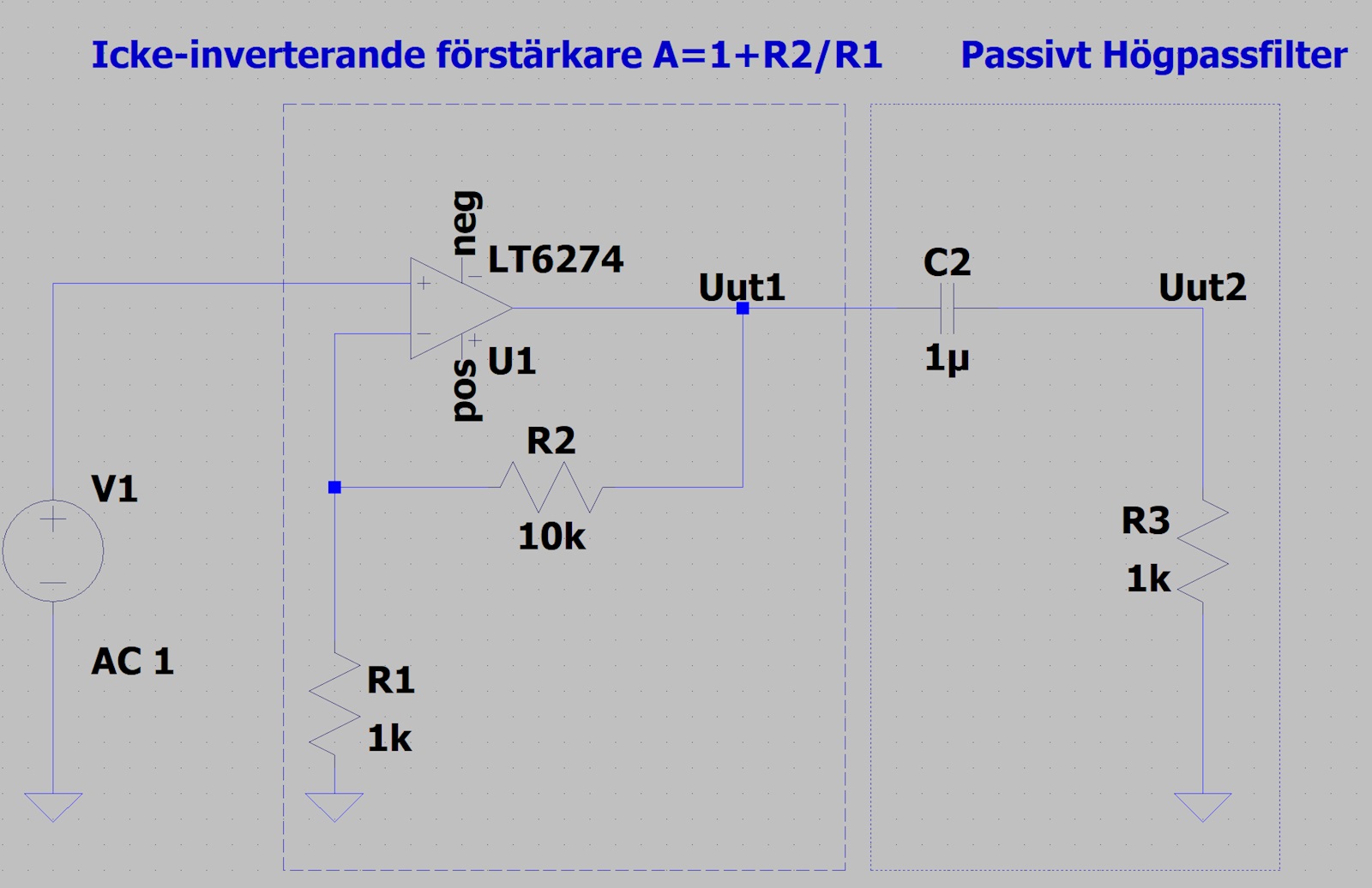
Om du generaliserar så kan förstärkningen för ovanstående icke-inverterande förstärkare skrivas som A=1+Z2/Z1 där Z1 och Z2 är impedanser istället för resistanser. Då inser du vad som skulle ske om man gjorde såhär:

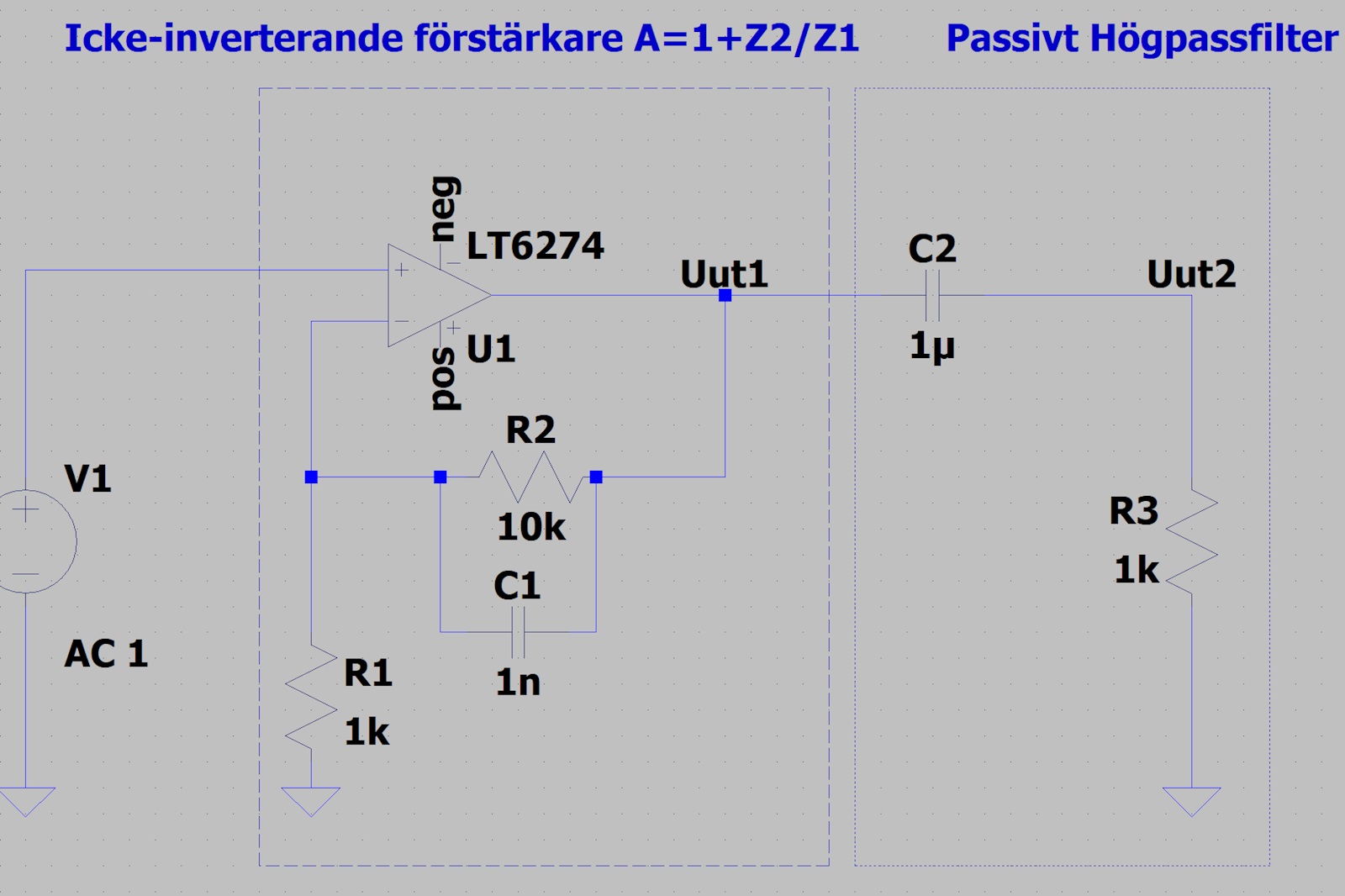
Om frekvensen går mot oändligheten så så kommer C1 att kortsluta R2, dvs impedansen Z2 går mot noll, och förstärkningen går mot ett. Slutsats: C1 gör så att den icke-inverterande filtret blir ett lågpassfilter (förstärkningen går mot ett vid höga frekvenser, vid låga frekvenser går den mot 11.). 

Tycker du att detta makar sense? På så sätt så kan man ofta se vilken slags karaktäristik ett filter får, om man tänker sig vad som händer med impedanserna (R, L och C) när frekvensen går mot noll och går mot oändligheten

Problemet med din uppgift är att den är inte speciellt realistisk. Någon klurade fram en uppgift utan att tänka på hur det skulle fungera i verkligheten. Eftersom om du tänker på samma sätt i din uppgift så ser du att impedansen Z2 går mot oändligheten när frekvensen går mot noll (C1 blir en öppen krets), vilket kommer att innebära att förstärkningen går mot oändligheten. Oändliga signaler är aldrig bra när det handlar om elektronik, eftersom verkligheten kommer att begränsa (operationsförstärkaren kommer att upphöra fungera). Hänger du med?

Men vi kan för en stund strunta i verkligheten och räkna uppgiften iallafall om du vill. Kan du ställa upp förstärkningsfunktionen med hjälp av de handritade ekvationerna (du behöver inte förenkla).

Du använder samma strategi för att snabbt identifiera vilken karaktäristik ett passivt filter har

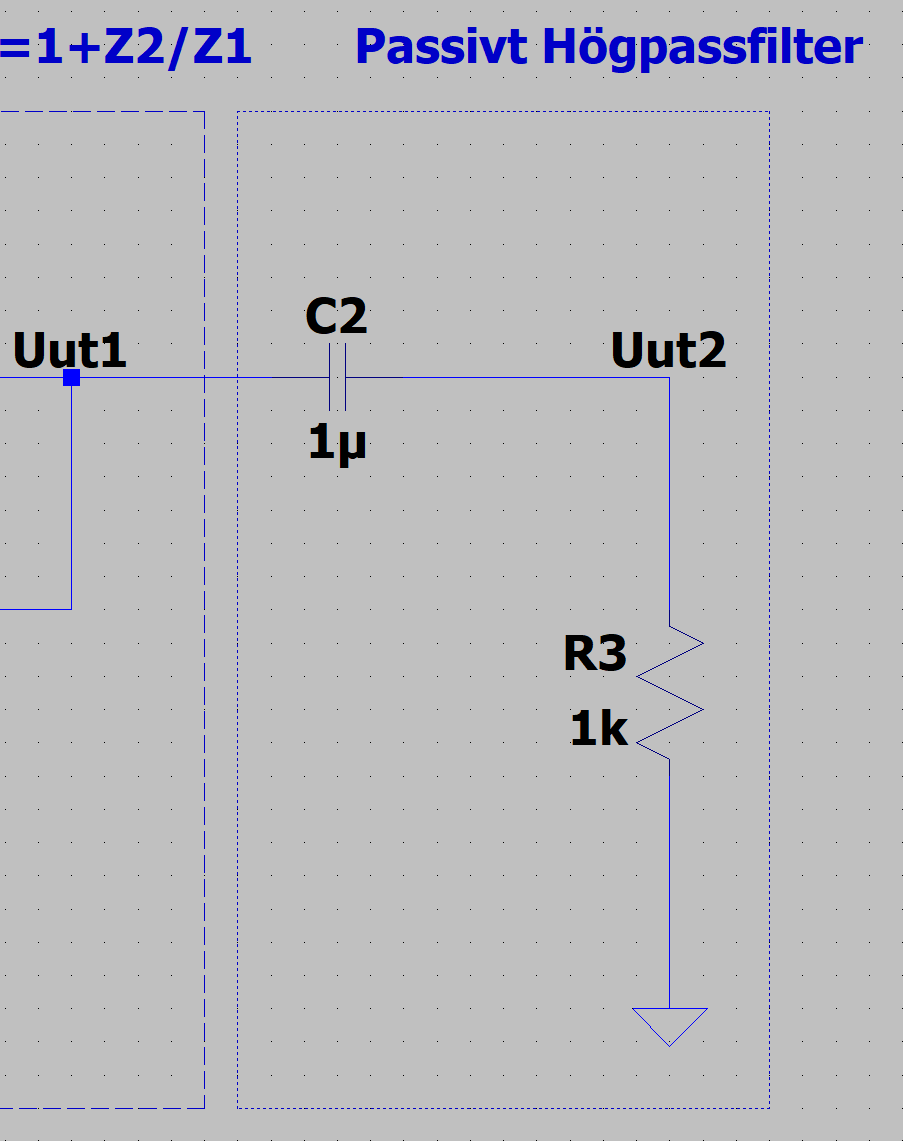
Detta passiva filter är bara en spänningsdelning mellan impedansen av C2, och R3. Om frekvensen går mot oändligheten så blir C2 en kortslutning, dvs all spänning hamnar över R3, dvs höga frekvenser släpps igenom. Låga frekvenser ger stor impedans över C2, dvs bara en liten del av spänningen hamnar över R3.

Om du generaliserar så kan förstärkningen för ovanstående icke-inverterande förstärkare skrivas som A=1+Z2/Z1 där Z1 och Z2 är impedanser istället för resistanser

Det där var onödigt otydligt uttryckt av mig. Det jag menar är att man kan jämföra standardförstärkarens förstärkningsuttryck med impedanser istället för resistanser för att få en snabb förståelse vad som kommer att hända när frekvensen går mot noll eller mot oändligheten, dvs asymptotiskt beteende, och därmed avgöra om det är hög pass lågpass bandpass etc.. 

Det exakta förstärkaruttrycket måste naturligtvis beräknas med jw eller något.

Vill minnas att Bodes normalform någotsånär såg ut som följande beräkningar intill kretsen.

Vilka förklaringar! Jag förstår nu!!!!

Jag är så tacksam, tack!

Min föreläsare älskar oändliga impedanser. Jag har aldrig riktigt tänk på att applicera beräkningarna till realiteten,  men det är ganska ofta dem går mot oändligheten, ja. Men super bra förklaring! Enoooooormt tacksam! Tack för tiden du la ner! 

Om du får tillfälle och vill, så tycker jag att du ska fråga din föreläsare om vad hen tror om förstärkarsteget med op-ampen. Även fast de kaskadkopplade filtren tillsammans ser ut att ge en "snäll" förstärkning för DC (då omega är noll) som J-R visade så kommer DC att mätta operationsförstärkaren på grund av den oändliga förstärkningen som C1 ger. När operationsförstärkaren mättas kommer verkligheten inte längre att följa teorin.

Jag håller med JohanF om att kretsen verkar lite konstig.

Observera att för spänningskvoten har jω förkortats bort mellan täljare och nämnare.

För höga frekvenser gäller uttrycket jag skrev, men inte för riktigt låga. Då måste ω vara kvar och kvoten blir 0/0 som är obestämt.