RC problem med 2 spänningskällor och beräkning av I(t)
Hej, jag skulle behöva lite hjälp på traven. Jag har fastnat och kan inte ta mig fram.
Detta är problemet:
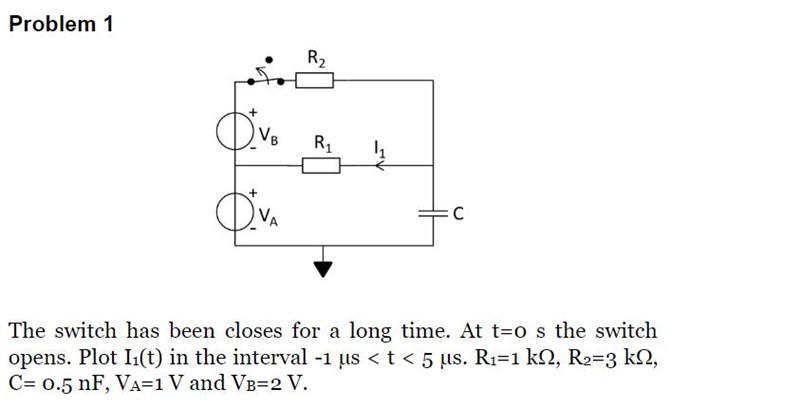
Jag har kommit såhär långt:

Jag har inte kommit så långt efter detta och anledningen för det är att jag inte riktigt vet hur jag ska förhålla mig till att hitta I1. Jag tänker att det är två fall: t<0 och t=0.
När det är t<0 så tänker jag att kapacitatorn bör agera som "open circuit" och då tänker jag att VA också försvinner (nu har jag inte ritat det i bilden), däremot tänker jag att I1 bör beräknas fram genom I1 = Vc/R1, men jag vet inte riktigt hur jag ska tänka mig fram när det kommer till att beräkna Vc och i sin tur beräkna I1.
Finns det några förslag hur jag ska tänka mig fram och hur jag ska förhålla mig till de två spänningskällorna?
Hej!
Jag tycker din figur för fallet t<0 är helt rätt. Kapacitansen har laddats upp till en spänning Vc och nu flyter inte längre någon ström in eller ut ur den. Helt rätt också att man ska räkna ut I1 men din ansats är nog fel väg att gå, vi vet ju inte vad Vc är.
Vad är det som driver strömmen I1 i detta läget? Tips: Strömmen in/ut från kapacitansen är...
När du har I1 kan du räkna ut Vc vid tiden 0 (precis innan switchen öppnas)
P.S. Jag har sett ibland att orden öppen och sluten när det gäller strömbrytare kan missförstås. Öppen betyder inte att vägen för strömmen är "öppen", och omvänt för sluten. Öppen menas att kontakterna är isär och strömmen är bruten.
Hej Thomas,
Det som driver strömmen I1 i fallet t<0 bör nog vara VB som är 2 V.
Så jag tänker att strömmen I1 bör vara 2/(1000+3000) = 0.5 mA.
Nu kan vi nog räkna ut Vc som blir 1 + (0.0005 * 1000) = 1.5 V.
Så Vc(0) bör vara 1.5 V ?
Hej igen,
Jag tänker även att när t<0, alltså när switchen öppnar att kapacitatorn kommer att urladdas till 1 V, alltså V(∞) = 1 V. Är jag helt ute och cyklar nu?
Nu händer det saker!
Då har du starttillståndet när switchen öppnas både för Vc och I1. Vad händer sedan när switchen öppnar?
Hej,
Har du sett det jag skrev efter mitt senaste inlägg?
Oj, där krockade vi lite.
V(oändl) = 1V. Helt rätt!
Nu vill jag beräkna I1 efter att switchen öppnar upp. Jag tänker att vi endast har nedre delen av kretsen som består av VA, R1 och C. Hur ska jag tänka nu med I1, är det så enkelt som Vc/R1 = 1/1000 = 1 mA?
Njaee. Det är bara den nedre delen kvar, helt riktigt, men du kommer att få en urladdning av kapacitansen från 1.5V ner till 1V. Strömmen I1 och spänningen Vc kommer att variera med tiden. Det är det där med e^(-t/RC) du vet.
Hittade en lite fin redogörelse för upp och urladdning av kapacitanser: https://jorjani.weebly.com/uploads/2/4/4/9/24491818/kondensator.pdf
Jo men precis. Jag tänker åter på formeln Vc(t) = V(∞) + [V(0) - V(∞)]e^(-t/tau), då tänker jag att det i mitt fall blir: Vc(t) = 1+[1.5-1]e^(-t/0.5us), däremot så vill frågan att jag ritar grafen för I1(t), det är lite där jag har svårt att förstå hur jag ska tänka för att få ut formeln.
Det är nog enklare än du tror. Vad får du för spänning över motståndet R1 under urladdningen? Sen är det bara ohms lag!
Är det inte 1 V som man får över R1? borde det då inte bli I1 = V/R = 1/1000 = 1 mA?
Spänningen över R1 blir ju Vc(t)-V(oändl). V(oändl) är ju samma som Va. Vc(0)=1.5V och Va=1V så du får en ström som börjar med 0.5mA och sedan minskar med tiden.
Jaha just det, jag måste ju tänka på VA också. Det glömde jag bort. Går det alltså att använda Vc(t) = V(∞) + [V(0) - V(∞)]e^(-t/tau), men för ström istället, eller blir det helt fel om man vill plota kurvan för ström?
Hej igen Thomas,
Nu är jag lite förvirrad. Jag tänker att denna ström vi fått fram på 0.5 mA är alltså I1(∞) = 0.5 mA. Detta gör mig förvirrad då I1 (0) = 0.5 mA, så då tänker jag att de både "starta" och fortsätter mot oändligheten som en rak streck bara, men det kan ju inte stämma i och med att kurvan antagligen kommer minska med tiden.
Jag rörde nog till det lite för dig. Om du kan skriva en formel för spänningen över R1 så löser sig det mesta.
Nåt sånt här: Vr1(t) = Vc(t)-Va = Va + [V(0) - Va]e^(-t/RC) - Va = [V(0) -Va]e(-t/RC)
Sen är det som sagt bara ohms lag kvar för att få strömmen.
Förlåt mig Thomas, jag har hängt med fram till att kapacitatorn urladdats vilket blev 1 V. Jag förstår inte riktigt vad som händer här om jag ska vara helt ärlig.
Jag försökte rita en kurva baserat på: Vc(t) = V(∞) + [V(0) - V(∞)]e^(-t/tau) = 1 +0.5e^(-t/0.5us)
Men jag fick en konstig kurva. Tror du att du kan förklara lite mer utförligare och visa med kurva som sist. Det hjälpte mig att förstå väldigt bra. Om det inte är till för mycket besvär.
Snabba ryck nu :-)
Det ser ut som du missar en parentes i sista ledet (1.5-1)e(-t/RC)
Ska ta och rita lite figurer också.
Hej igen
Här kommer en figur från en simulering:
.jpg?width=800&upscale=false) Gäller för t>0. (Kanske lite fuskigt att att använda simulering)
Gäller för t>0. (Kanske lite fuskigt att att använda simulering)
Tack för simuleringen. Dock är jag fortfarande fast på hur du fått till kurvorna. Är det verkligen (1.5-1)e(-t/RC) du använder för att få fram kurvan för strömmen?
Nu är det sådär jobbigt att min tankegång inte går fram >.<
Jag förstår exakt hur kurvan skapas för spänningen. Jag använder mig av 1 + 0.5e^(-t/RC). Däremot blir jag som sagt inte klok på ström kurvan...
Du är så nära så nära.
Du är med på att Vc(t) är spänningen över kapacitansen och den startar på 1.5V och sjunker med tiden ner till 1V?
Då kommer spänningen över R1 att vara just: Vr1(t) = (1.5-1)e(-t/RC)
Då blir ju strömmen I1(t) = Vr1(t)/R1
I1(0) = 0.5V/1kohm = 0.5mA
I1(0.5us) = 0.184V/1kohm = 0.184mA
I1(1us) = 0.068V/1kohm = 0.068mA
osv
Oh tack!!! Nu fattar jag!! =D
Min allra sista fråga är bara på intervallet, att det just börjar på -1 us, jag får det till I1(-1) = 3.6945V/1kohm = 3.69 mA. Kan det verkligen stämma?
Eller kan det vara att det är 500 uA eftersom villkoret är t<0, så att allt innan t=0 blir en rak sträcka så att säga?
Jag fick det till det här:
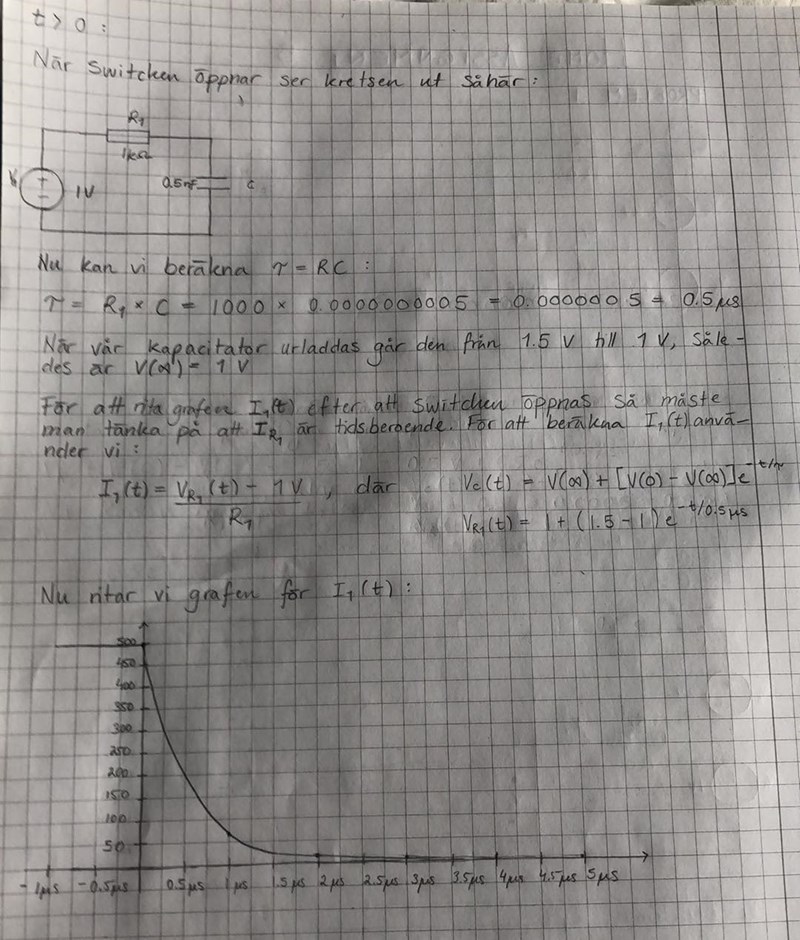
Formeln gäller bara för t>0.Dvs efter switchen har öppnat.
Innan switchen öppnar gäller andra förutsättningar. I och med att switchen har varit sluten "länge" får man förutsätta att vi hamnat i ett "steady state" där spänningen över kapacitansen har stabiliserat sig på 1.5V och inget annat heller varierar med tiden. Så strömmen vid -1us är den samma som till precis innan switchen öppnar vid t=0.
Jag måste säga att jag är imponerad av din envishet och vilja att förstå. Alla tummar upp!
Tackar!! Jaa jag förstod det efter att jag tänkte igen.
Tack så jättemycket!! Det är kul att lära sig när någon pushar en att använda alla hjärnceller som finns! =D
Sorry om jag varit lite jobbig, men jag hatar att lämna uppgifter halvdana utan att förstå!
Inget att be om ursäkt för, rätt inställning!


