Reglerteknik

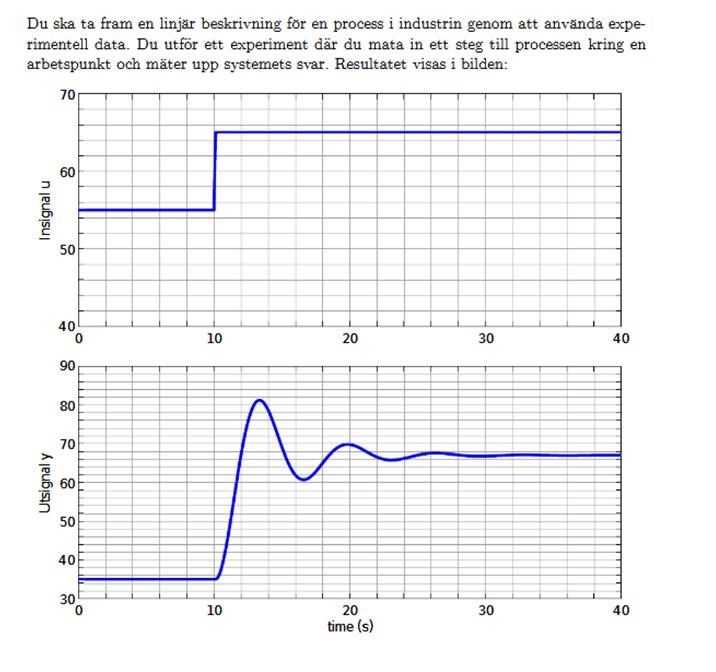
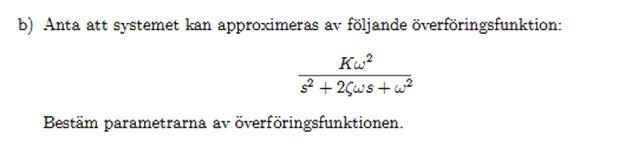
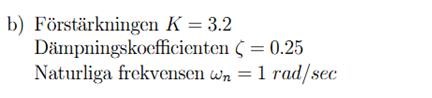
Jag kan bara ge dig ett tredjedels svar, jag är alltför ringrostig i reglertekniken.

K är väl förstärkningen. Den kan man väl få fram om man tittar på förhållandet Utsignal/Insignal när alla tidsvariabla förlopp har klingat av, dvs i högerkanten på kurvorna.

Nu är jag inne på gissningar här, men kan w_n fås från svängningstiden?

Tiden mellan topparna är ca 6s. f_n = 1/6 och w_n = 2*pi*f_n = 6.28/6 ~ 1 rad/s

Som sagt detta är gissningar.

Tack för svaret. Nu förstår jag c.

Men jag har fortfarande svårt att förstå hur de har fått k till 3,2.

Fick du fram dämpningskoefficienten? Nu blir jag nyfiken.

Förstärkningen K:
Om man läser i diagrammen så gör insignalen ett steg från 55 till 65 dvs 10 enheter.
Utsignalen går från 35 till 67 dvs 32 enheter. (Lite trixigt att läsa i det diagrammet).
Utsignal/Insignal = 3.2

Tack för en bra förklaring.

Nej har inte lyckats förstå hur de har kommit fram till svaret till dämpningskoefficienten. Får läsa lite till.  Återkommer när jag har lyckats lösa den.

Med slutvärdessatsen går det att se att förstärkningen är K då t går mot oändligheten. Det är därför korrekt titta på kvoten utsignal/insignal då förlopp klingat av. Får att få fram $\omega_n$ går det att undersöka periodtiden $T=\frac{2\pi }{{\omega }_d}$ mellan topparna där $\omega_d=\omega_n\sqrt{1-\zeta^2}$. För att få fram $\zeta$ skulle man kunna titta på överslängen $M=e^{-\alpha}$ där $\alpha=\frac{\pi\zeta}{\sqrt{1-\zeta^2}}$.

Tack för hjälpen!