Rekursionsekvation (3)

"En talföljd definieras enligt $a_{n} = 6 a_{n - 1} - 9_{a - 2}, a_{0} = 1, a_{1} = 9$ sådan att då $n \geq 2$ . Visa att talen i följden kan beräknas med formeln $a_{n} = (1 + 2 n) 3^{n}$ ."

Sedan står det "lös endast ekvationen, vilket jag tolkar som att man ska lösa rekursionsekvationen, vilket jag inte får rätt på:

/🐎

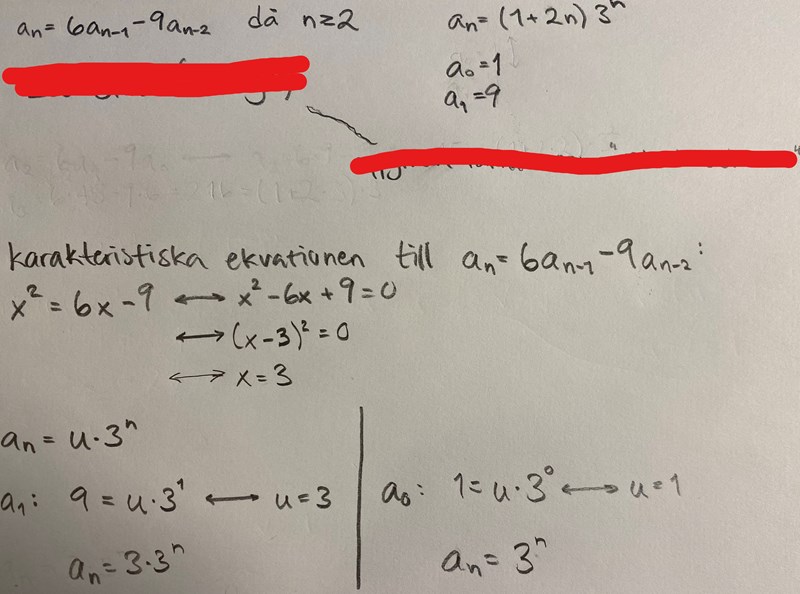
Du har dubbelrot, med allmän lösning:

$a_n=(An+B)3^n$ .

Hur får du fram den formeln? Är det inte $a_{n} = (A + B) 3^{n}$ ? Var kommer $A n$ ifrån?

Plugghingsten skrev:
Hur får du fram den formeln? Är det inte $a_{n} = (A + B) 3^{n}$ ? Var kommer $A n$ ifrån?

Hur man härleder den vet jag inte, men det är uppenbart att det inte räcker med A+B, för det är bara en konstant det också, så vi kan ersätta den med t.ex. C.

Okej. Efter att ha googlat runt lite har jag förstått det som att man inte heller ska räkna sig till denna formel utan kunna den/få den på formelsamling.

Med differentialekvationer uppträder samma sak.

Svara

Visa senaste svar