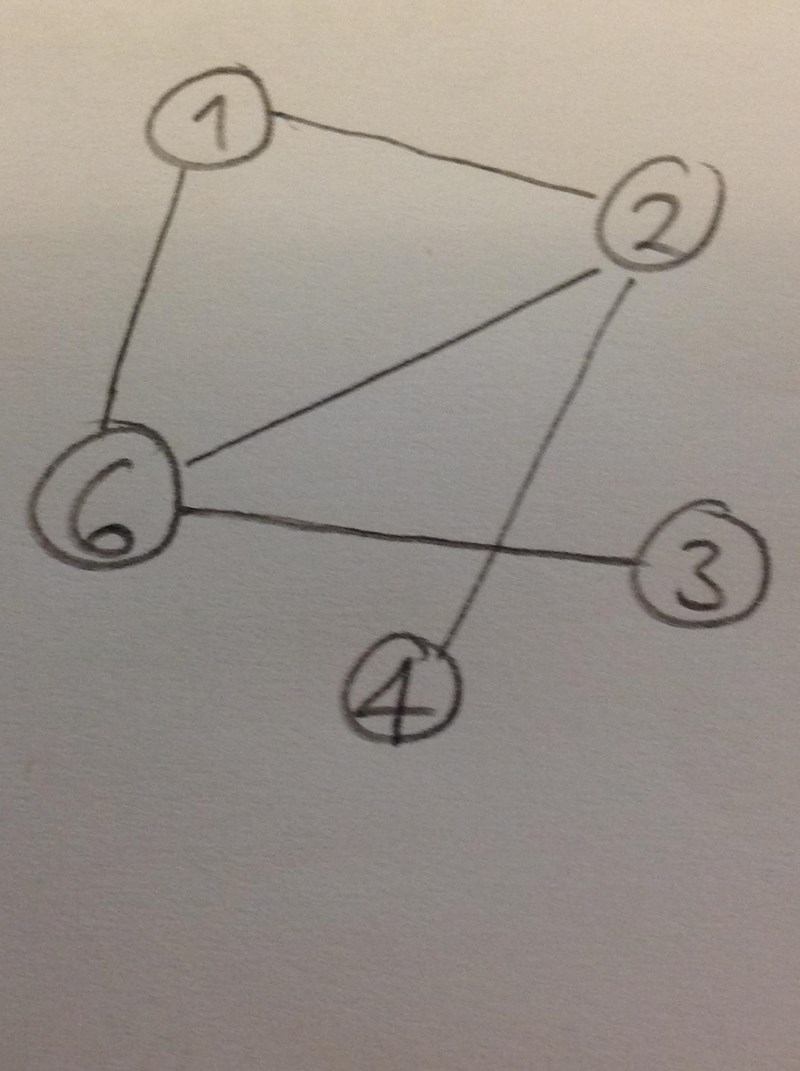
Relationer (2)
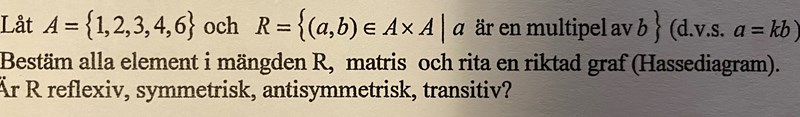
Alla elementen får jag till
Därifrån ser jag att är reflexiv och transitive men varken symmetrisk eller antisymmetrisk. Jag är osäker på om det räknas som antisymmetrisk om bara någon av punkterna, som i detta exempel mellan 1 och 2 finns bara en riktning, har en riktning. Någon som kan förklara? Svaret är att den är reflexiv, transitive och antisymmetrisk.
Antisymmetri innebär att om det finns någon symmetrisk koppling mellan noderna A och B, måste nod A = nod B. Ett enkelt relationsdiagram över situationen:
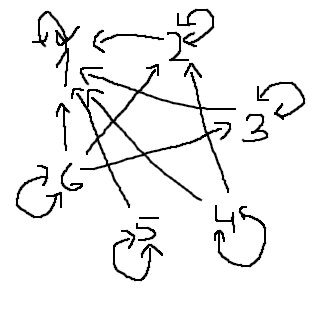
De enda symmetriska relationerna som finns är på formen (a, a), vilket är godkänt inom antisymmetrin, eftersom det är samma nod i båda ändar. Annars finns inga symmetriska relationer i diagrammet. :)
Där ser man! Tack för din kommentar, @Smutstvätt!
Det var så lite! ^ ^
Ursäkta om jag tar upp denna igen men om jag ska rita ett Hassediagram på denna, vet du/någon hur det skulle se ut? Är mitt lösningsförslag rätt: