Relativitetsteori - formel till rörelsemängd?
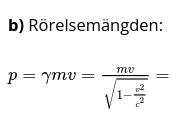
Undrar hur jag ska komma till denna formel ovan?
I min formelsamling står följande under rubriken relativitetsteori:

Ersätt med uttrycket för
ja den förstår jag men hur ska jag komma fram att rörelsemängd p = γ * m * v ?
Menar du något sådant här:
http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/relmom.html#c4
ja, fast tvärtom då har jag inte den i min formelblad. Kan man gå baklänges till formeln?
Ja, du kan lösa ut från , där
Men det är bättre att lära sig att och använda det som en definition av rörelsemängden.
Jag försökte att lösa ut den men får inte samma formel:
E2=(mc2)2+(pc)2
γmc2 =(mc2)2+(pc)2
γmc2 - m2c4 = p2c2
c2 (γm - m2c2) = p2c2
(γm - m2c2)= p2
(m
ELLER:-
= p
Hur ska jag gå vidare?
Du har glömt kvadrera vänster sida
Dela med och lös ut
Dra roten ur båda sidor och använd till exempel
Nja, det blir
Eftersom


