Resultera summan någonsin i ett primtal?

Denna summa är aritmetisk, vad blir den slutna formen för den? 

Ofta brukar det vara lättare att undersöka. 

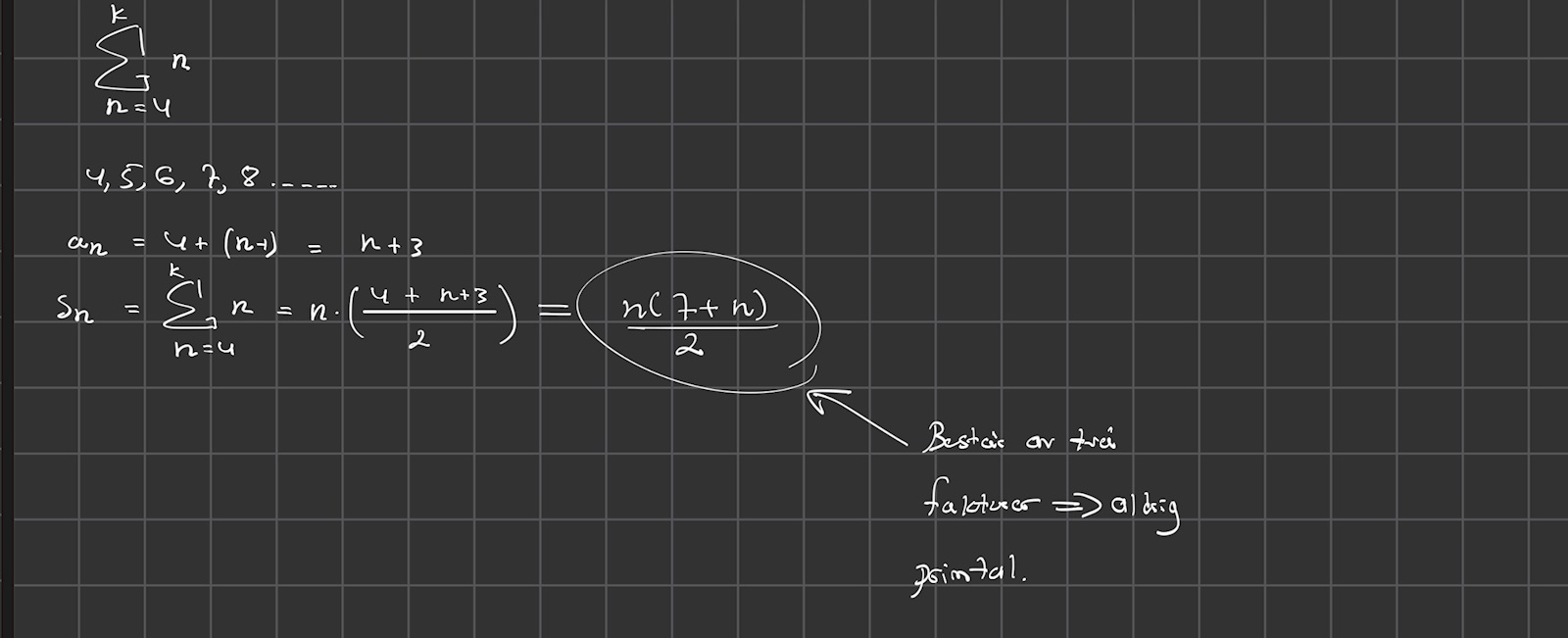Jag gjorde så här. Stämmer det? Ska man titta på gränsvärdet istället?

Facit:

Förstår ej hur de kommer fram till an?

Jag tror inte summaformeln är helt korrekt (också jag antar att ditt $k$ i toppen av summan $n$?) Jag fick

$\displaystyle\sum_{k=4}^n k = \frac{n(n+1)}{2}- 6 = \frac{\left(n-3\right)\left(n+4\right)}{2}$

Hur som helst, bara att det består av två faktorer betyder inte direkt att det inte är primtal. En av faktorerna kan vara $1$. Vidare, divisionen med $2$ ger att man behöver göra lite mer jobb (en av talen på toppen kan möjligtvis vara $2$) för att komma fram till om summan kan bli ett primtal eller ej.

Anonym_15 skrev:

Förstår ej hur de kommer fram till an?

Själv ogillade jag formelnotationen som användes i matte 5. Jag är också lite osäker på vad de gör. 

Vi kan säga att

$\displaystyle \sum_{k=4}^n k = 4 + 5 + \dots + n = \left(1+3\right) + \left(2+3\right) + \dots + \left(n-3 + 3\right) = \sum_{k=1}^{n-3}\left(k+3\right)$

Härifrån kan vi använda formeln för summan av de första $n$ heltalen. Min tankegång är att

$\displaystyle \sum_{k=4}^n k = -6+ \sum_{k=1}^n k = -6 + \frac{n(n+1)}2$

Alltså adderade jag $1+2+3$ in i summan och sedan subtraherade bort det för att ha kvar likhet. 

Med inspiration av AlexMu,

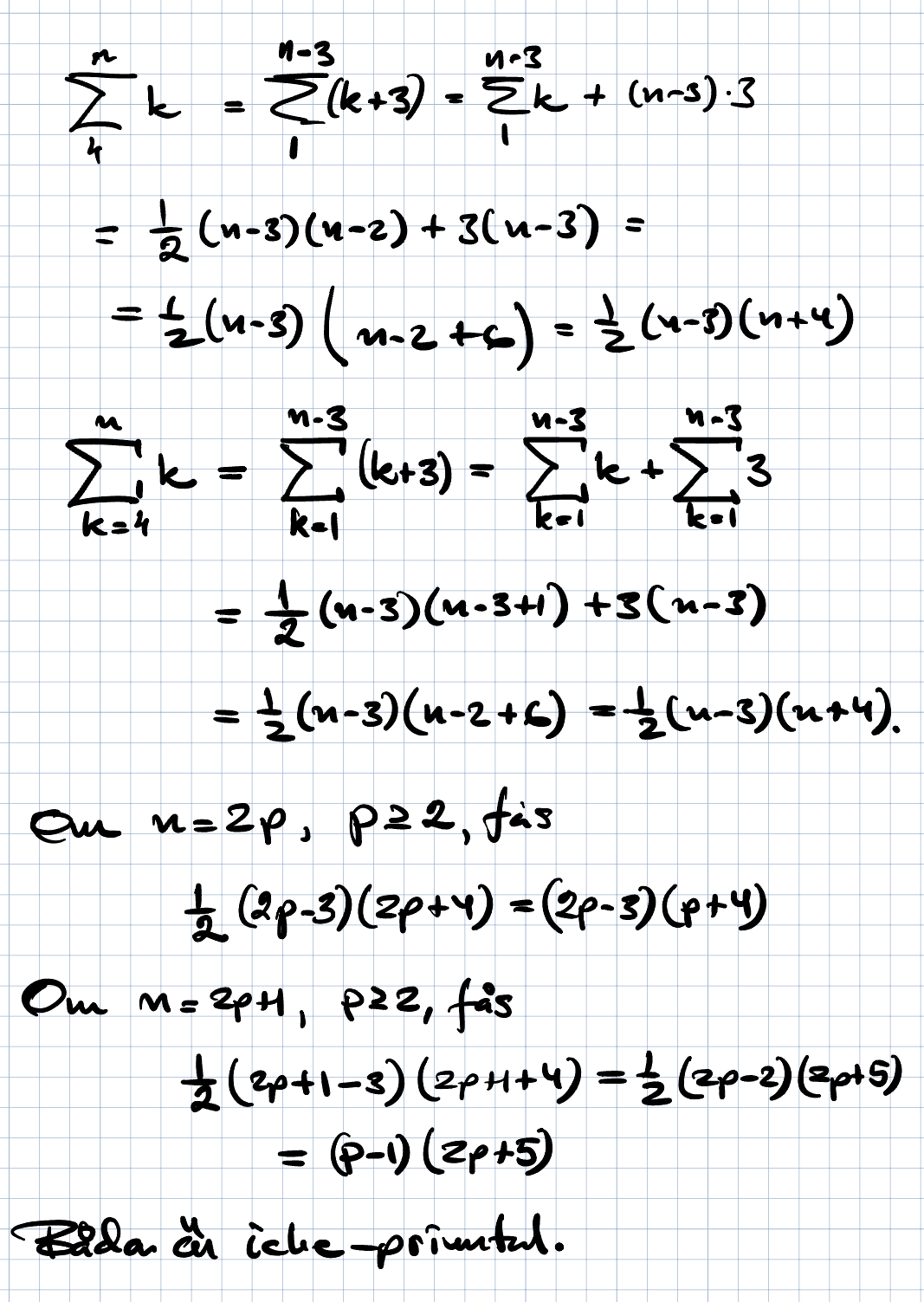
Anonym_15 skrev:

Facit:

Förstår ej hur de kommer fram till an?

Är detta handskrivna från facit?

Men hur kommer ni fram med denna formel för an? i vårt formelblad står följande för aritmetisk talföljd: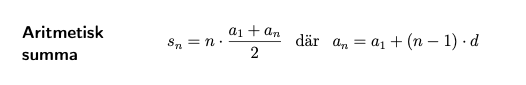

Då måste väl a1 = 4?

Den där summaformeln säger att

$\displaystyle \sum_{k=1}^n a_k = n \frac{a_1 + a_n}{2}$. 

Men, vi har inte en summa från $k=1$ till $n$. Vi måste göra lite extra arbete för att få det på den formen. 

Antingen kan vi notera att 

$\displaystyle \sum_{k=4}^n k = \sum_{k=1}^{n-3}\left(k+3\right)$

och nu kan vi använda summaformeln. Eller så kan vi använda att

$\displaystyle \sum_{k=4}^n k = -6+\sum_{k=1}^{n}k$ 

Nu är summaformeln också giltig. 

Den viktiga skillnaden är att vi skriva summan på ett visst sätt för att vi ska kunna använda summaformeln från ditt formelblad. 

Tack!