Riemann Sphere which corresponds to the point z=u+iv under stereographic projection.

Jag vet inte på rak arm, men den här artikeln nämner stereografisk projektion också: https://en.wikipedia.org/wiki/Riemann_sphere.

Laguna skrev:

Jag vet inte på rak arm, men den här artikeln nämner stereografisk projektion också: https://en.wikipedia.org/wiki/Riemann_sphere.

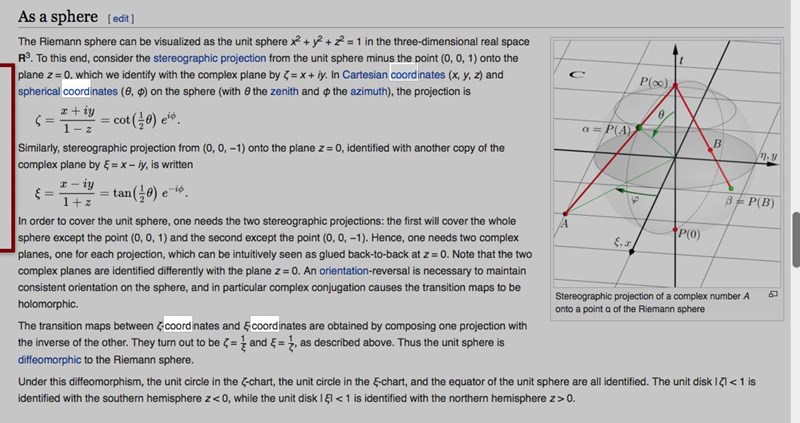
Då verkade denna intressant.  Men om jag då tar z=a+bi och de står " ζ-coordinates and ξ-coordinates are are obtained by composing one projection with the inverse of the other. They turn out to be ζ = 1/ξ and ξ = 1/ζ, as described above. Thus the unit sphere is diffeomorphic to the Riemann sphere."

Och då ska jag använda denna formel??? 

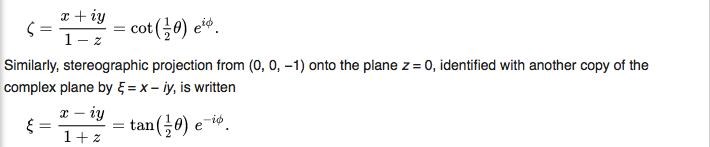
så då har jag ζ (vad heter denna btw?) , ζ = (a+bi)/(1-z) men vad är z då.  Det kan ju omöjligt va den samma som i uppgiften? eftersom z=a+bi. 

$\zeta$ heter zeta.

Har du läst på denna hemsida:

http://mathonline.wikidot.com/the-riemann-sphere

Där har du hursomhelst utvecklingen av resonemanget du förde ovan och resultatet det hade lett till längst ned på sidan. För varje komplext tal $z=x+iy$ finns en motsvarande punkt $P=(x_1, x_2, x_3)$ på Riemannsfären genom stereografisk projektion. Punkten ifråga hittas genom att dra en linje från $z$ till "Nordpolen"; skärningspunkten med sfären blir då punkten P. Koordinaterna blir då:

$x_1=\frac{2x}{1+{\left|z\right|}^2} x_2=\frac{2y}{1+{\left|z\right|}^2} x_3=\frac{{\left|z\right|}^2-1}{1+{\left|z\right|}^2}$

Ebola skrev:

Har du läst på denna hemsida:

http://mathonline.wikidot.com/the-riemann-sphere

Där har du hursomhelst utvecklingen av resonemanget du förde ovan och resultatet det hade lett till längst ned på sidan. För varje komplext tal $z=x+iy$ finns en motsvarande punkt $P=(x_1, x_2, x_3)$ på Riemannsfären genom stereografisk projektion. Punkten ifråga hittas genom att dra en linje från $z$ till "Nordpolen"; skärningspunkten med sfären blir då punkten P. Koordinaterna blir då:

$x_1=\frac{2x}{1+{\left|z\right|}^2} x_2=\frac{2y}{1+{\left|z\right|}^2} x_3=\frac{{\left|z\right|}^2-1}{1+{\left|z\right|}^2}$

så denna, 

då gör jag : 

(1) $[(3t)]^2+[5t]^2+[1-t)]^2=1$ detta blir ju skärningen som jag förstått det. 

som ger mig $t = 0$ and $t = 2/35$

ska jag substituera in dom då i (1)  nääe.

Jag tycker du har börjat mycket bra i ditt första inlägg. Vi har ju en punkt $P$ i det komplexa talplanet motsvarande $z=a+bi$ och sedan drar vi en linje genom denna punkt och nordpolen $N$ på Riemannsfären och söker skärningspunkten $A$ med Riemannsfären:

Med metoden vi lärde oss i linjär algebra kan vi skriva linjen på parameterform genom att ta en riktningsvektor och en punkt på linjen. I detta fall blir riktningsvektorn $PN$ lika med $(a,b,0)-(0,0,1)=(a,b,-1)$ och punkten på linjen kan vi helt enkelt välja som nordpolen $N=(0,0,1)$. Linjen ges alltså på parameterform av:

$(\xi,\eta,\zeta)=t(a,b,-1)+(0,0,1)=(at,bt,1-t)$

Nu vill vi alltså ta reda på denna linjes skärningspunkter med Riemannsfären. Detta gör vi genom att sätta in $\xi$, $\eta$ och $\zeta$-värdena i ekvationen:

$\xi^2+\eta^2+\zeta^2=1$

$(at)^2+(bt)^2+(1-t)^2=1$

och lösa ut för $t$-värdena. När du löst ekvationen kommer du att få fram två $t$-värden som kommer ge punkten $N$ och punkten $A$ när du stoppar tillbaka dem i parameterformen för linjen.

AlvinB skrev:

Jag tycker du har börjat mycket bra i ditt första inlägg. Vi har ju en punkt $P$ i det komplexa talplanet motsvarande $z=a+bi$ och sedan drar vi en linje genom denna punkt och nordpolen $N$ på Riemannsfären och söker skärningspunkten $A$ med Riemannsfären:

Med metoden vi lärde oss i linjär algebra kan vi skriva linjen på parameterform genom att ta en riktningsvektor och en punkt på linjen. I detta fall blir riktningsvektorn $PN$ lika med $(a,b,0)-(0,0,1)=(a,b,-1)$ och punkten på linjen kan vi helt enkelt välja som nordpolen $N=(0,0,1)$. Linjen ges alltså på parameterform av:

$(\xi,\eta,\zeta)=t(a,b,-1)+(0,0,1)=(at,bt,1-t)$

Nu vill vi alltså ta reda på denna linjes skärningspunkter med Riemannsfären. Detta gör vi genom att sätta in $\xi$, $\eta$ och $\zeta$-värdena i ekvationen:

$\xi^2+\eta^2+\zeta^2=1$

$(at)^2+(bt)^2+(1-t)^2=1$

och lösa ut för $t$-värdena. När du löst ekvationen kommer du att få fram två $t$-värden som kommer ge punkten $N$ och punkten $A$ när du stoppar tillbaka dem i parameterformen för linjen.

Jag får ut ett värde då ju, om jag tar exemplet: https://www.wolframalpha.com/input/?i=(3(2%2F25))%5E2%2B(5(2%2F25))%5E2%2B(1-2%2F25)%5E2

Jag vet inte riktigt vad du försöker säga att du får ut. Om du stoppar in $a=3$ och $b=5$ får du $t$-värdet $2/35$.

Vad får du för punkt om du stoppar in $t=2/35$ i den parametriserade linjen?

AlvinB skrev:

Jag vet inte riktigt vad du försöker säga att du får ut. Om du stoppar in $a=3$ och $b=5$ får du $t$-värdet $2/35$.

Vad får du för punkt om du stoppar in $t=2/35$ i den parametriserade linjen?

Jag får ut ett värde: 

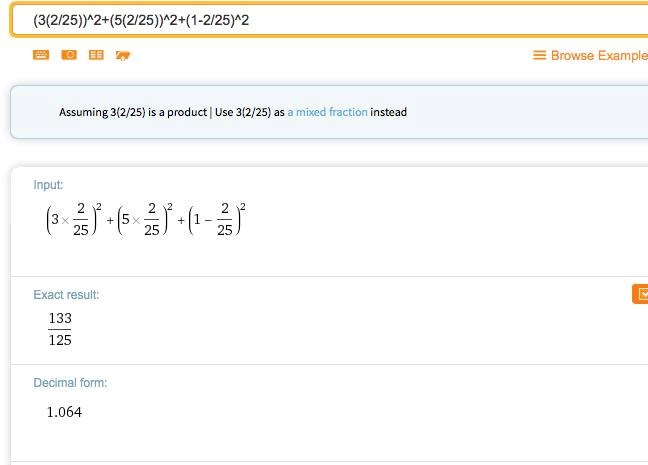
(såg nu att jag skrivit 25 istället för 35) och jag ska (eller, enl bilden) ha 3 st koordinater)

Jo, men om du gör som jag säger och stoppar in $t=2/35$ i parametriseringen får du en punkt med tre koordinater, precis som du vill ha.

Dessutom bör du vara medveten om att $t=0$ även är en lösning till ekvationen, men att vi ignorerar den eftersom den motsvarar nordpolen $N=(0,0,1)$.

AlvinB skrev:

Jo, men om du gör som jag säger och stoppar in $t=2/35$ i parametriseringen får du en punkt med tre koordinater, precis som du vill ha.

Dessutom bör du vara medveten om att $t=0$ även är en lösning till ekvationen, men att vi ignorerar den eftersom den motsvarar nordpolen $N=(0,0,1)$.

jaaaaa sorry, trög!!