Riemensumma envariabelsanalys
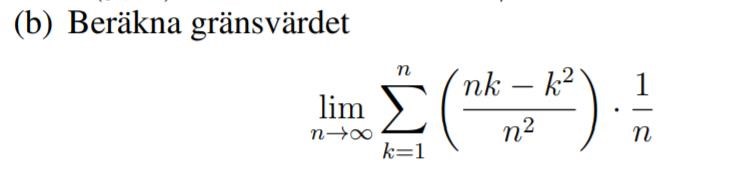
Uppgiften handlar om riemensummor dess gränsvärde. Jag har kommit fram till att det är en undersumma som sökes och att "summeringsgränserna" är n och k=1. Någon som har en idé om hur jag kan tänka?
Vi vill skriva om serien som en integral . En kvalificerad gissning är ju att börja med att identifiera att är bredden på alla våra ''staplar'' i Riemannsumman. Eftersom vi antar att alla dessa staplar har samma bredd har vi så , d.v.s. längden på intervallet vi integrerar över ska vara 1. Om vi nu skriver så ser vi att summan vi ska ta gränsvärdet av ser ut enligt . Kommer du vidare?
Jag fick 1/6, är svaret korrekt?
Freewheeling skrev:Vi vill skriva om serien som en integral . En kvalificerad gissning är ju att börja med att identifiera att är bredden på alla våra ''staplar'' i Riemannsumman. Eftersom vi antar att alla dessa staplar har samma bredd har vi så , d.v.s. längden på intervallet vi integrerar över ska vara 1. Om vi nu skriver så ser vi att summan vi ska ta gränsvärdet av ser ut enligt . Kommer du vidare?
Tack så mycket för hjälpen jag förstod nu när jag såg integralen omskriven!
Ett sätt att kontrollera:
Detta ger (ledande termen):
Bernhard Riemann (1826-1866),
"mest känd för att ha formulerat den första rigorösa integralen,
den så kallade Riemannintegralen" och det är inte det enda
han är berömd för.
https://sv.wikipedia.org/wiki/Bernhard_Riemann
[kort idéhistorisk notis a propos denna uppgift...]


