Riktningskoefficient

Nej. Du ska räkna lutningen i punkten (3,-5). Ett tips är att rita först.

Jag deriverade funktionen f(x). Då blev det f’(x)=-2x 

i punkten då x=3 gäller det f’(3)=-2*3=-6

Hur ska jag göra? Jag har ritat men det underlättar inte för mig

Lisa14500 skrev:

Jag deriverade funktionen f(x). Då blev det f’(x)=-2x 

i punkten då x=3 gäller det f’(3)=-2*3=-6

Hur ska jag göra? Jag har ritat men det underlättar inte för mig

Som du räknat nu så har du fått fram k för tangenten i punkten (3,-5). När du ritat kurvan och tangenten så kan du se hur många steg i y-led ett steg i x-led motscarar för tangenten. Det är din lutning och k-värde. Ser det ut att stämma överems med det du räkant ut?

Nej jag förstår inte. Vad säger f’(3)? Är det lutningen vid punkten x=3 som vi räknar ut? 

Lisa14500 skrev:

Nej jag förstår inte. Vad säger f’(3)? Är det lutningen vid punkten x=3 som vi räknar ut? 

Ja precis, derivatan för funktionen f(x) dvs. f'(x)  är lutningen för f(x) i respektive punkt. Så för f'(1) så har du lutningen för f(1) etc. Jämför med derivatan av en rät linje. Det blir en konstant och är således samma för alla x. (Precis som en rät linje är)

Okej så när det står ”räkna ut lutningen då x=3” då ska man räkna ut derivatan och därefter sätta f’(3) vilket betyder ”lutningen vid just den punkten”

Ja. Rita in den linjen i samma bild som din parabel, så ser du att de lutar lika mycket.

Jag får svaret y=-6x+23. Är det rätt?

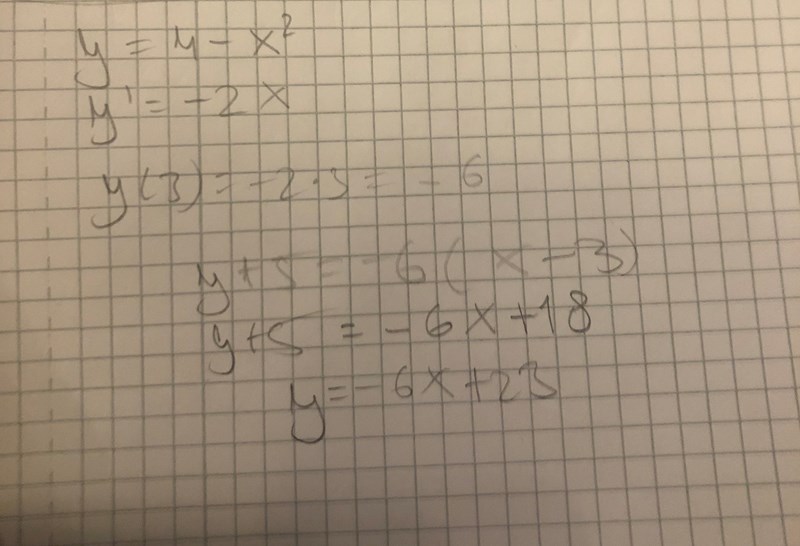
Rita och se efter! Om du behäver hjälp med attse om det sätmmer, kan du lägga upp bilden här.

Nej jag ser att svaret inte stämmer... Vart är felet?

Du har fått fram

y+5=-6x+18,

dra bort 5 på båda sidor och du får

y=-6x+13.

Låt oss dubbelkolla svaret. Lutningen är -6, vilket stämmer.

Om x = 3 så får vi y=-6$·$3 + 13 = -5, vilket också stämmer.

Så vi har fått fram tangentens ekvation. Men vad frågades det efter i frågan? Vad skall vi svara?

Jag tror att jag har lyckats lösa uppgiften. Den här gången har jag en förståelse för varför man ska göra på ett visst sätt. 

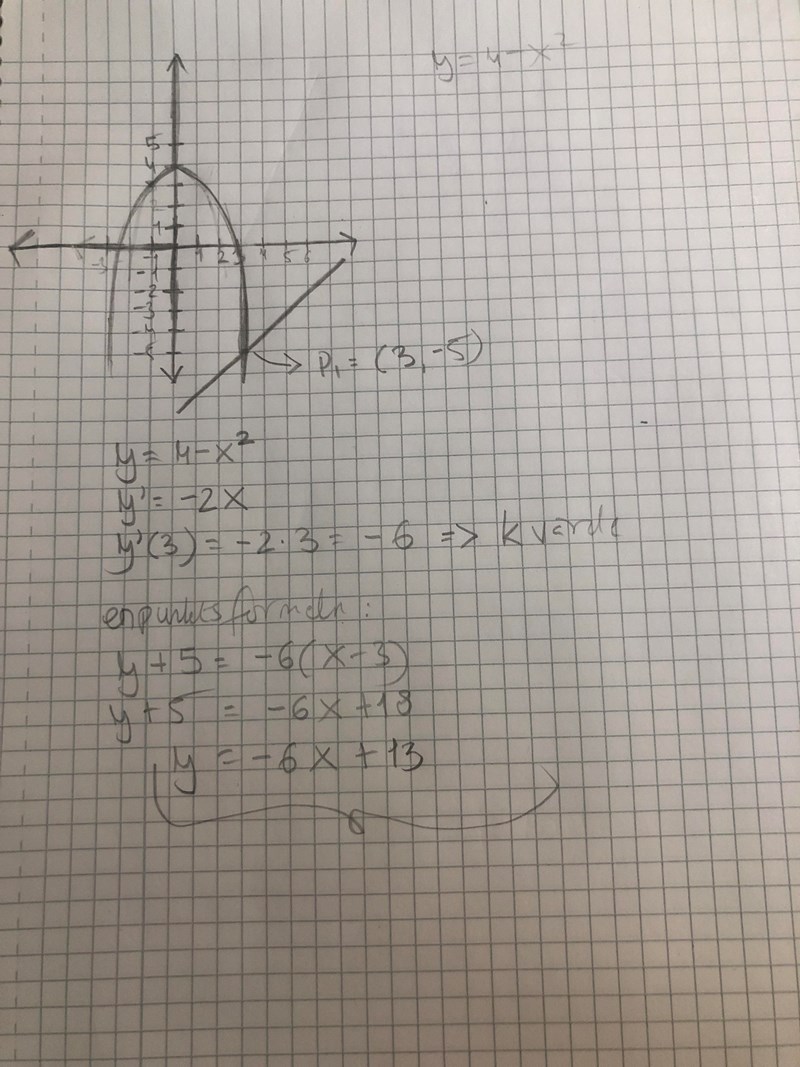Riktningskoefficienten blir -6

Ditt svar är rätt. Bra!

Men vad är det för linje du har ritat i figuren?

En tangent 

Det är det inte. En tangent tangerar, alltså nuddar bara, inte skär igenom.

Lisa14500 skrev:

En tangent 

Det stämmer inte alls. Varför har du valt just den riktningen för tangenten?

Nu blir jag orolig att du inte alls vet vad en tangent är?

Läs hela det här avsnittet, speciellt det som står på slutet om vad en tangent är:

"När man har en linje som berör en kurva i endast en punkt och har samma lutning som kurvan i den punkten, då säger man att denna linje tangerar kurvan och att den bildar en tangent till kurvan i den gemensamma punkten."

Jag vet vad en tangent är men där slarvade jag lite. Ni har rätt att en tangent endast ska nudda grafen vid en viss punkt 

Lisa14500 skrev:

Jag vet vad en tangent är men där slarvade jag lite. Ni har rätt att en tangent endast ska nudda grafen vid en viss punkt 

... och ha samma lutning som grafen i den punkten.

Kan du lägga in en ny bild som visar parabeln och tangenten?