rita i det komplexa talplanet
Markera i en figur de komplexa tal, z, som uppfyller följande villkor:
- ∣z-3∣< 1 , om Imz > 0
- ∣z+1∣≤ 5, om Imz ≤ 0
jag ritade figuren på andra hållet, alltså markerade -3 och 1 sedan en cirkel omring dem vilket ör fel men jag förstår inte varför?
facit: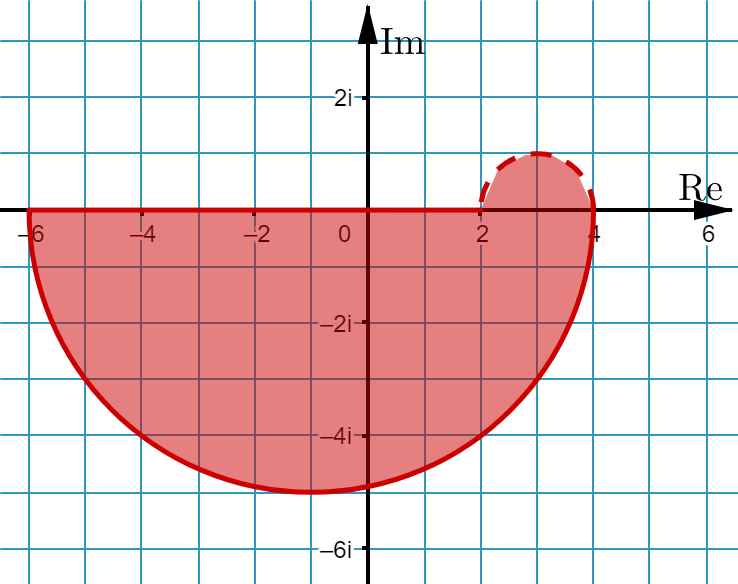
För att olika saker gäller om vi är på den positiva eller negativa Im-delen, alltså ovanför eller under Re-axeln.
MrPotatohead skrev:För att olika saker gäller om vi är på den positiva eller negativa Im-delen, alltså ovanför eller under Re-axeln.
jag hänger inte med, vad är det den -3an och 1an egentligen gör?
bolibompa skrev:
jag hänger inte med, vad är det den -3an och 1an egentligen gör?
Ekvationen z-3 = 0 har lösningen z=3 (man brukar säga att 3 är en rot av ekvationen).
Olikheten |z-3| < 1 har lösningar nära 3, när avståndet till z=3 är mindre än 1, alltså innanför ett cirkel med radie 1 kring z=3.
Pieter Kuiper skrev:bolibompa skrev:
jag hänger inte med, vad är det den -3an och 1an egentligen gör?Ekvationen z-3 = 0 har lösningen z=3 (man brukar säga att 3 är en rot av ekvationen).
Olikheten |z-3| < 1 har lösningar nära 3, när avståndet till z=3 är mindre än 1, alltså innanför ett cirkel med radie 1 kring z=3.
ok tack, nu blev det tydligt!



