Rita i komplexa talplanet
Hej! Kan någon snälla hjälpa mig med den här uppgiften?
''Rita upp ett komplext talplan och visa lösningarna till nedanstående uppgifter''
a. / z-1 / < 4
b. / z-2i / = /z -10i /
hur ska jag tänka???
Börja så här: markera talet 1 i komplexa talplanet. (Varför 1? Jo, för att det står z - 1.) Visa bilden här.
b tar vi senare.
|z-1| kan tolkas som avståndet mellan talet z och talet 1. Vad beskriver då den första olikheten?
Skaft skrev:|z-1| kan tolkas som avståndet mellan talet z och talet 1. Vad beskriver då den första olikheten?
att avståndet mellan talet z och 1 är mindre än 4, men förstår bara inte hur jag ska rita upp det
Betrakta . Vad är detta för geometrisk figur?
Du kan ansätta och räkna på. Använd räkneregler för komplexa tal.
melinasde skrev:Skaft skrev:|z-1| kan tolkas som avståndet mellan talet z och talet 1. Vad beskriver då den första olikheten?
att avståndet mellan talet z och 1 är mindre än 4, men förstår bara inte hur jag ska rita upp det
Nästan så, men tänk plural istället: eftersom en ekvation (eller olikhet) kan ha flera lösningar är inte z nödvändigtvis ett enda tal. Olikheten beskriver alla komplexa tal som ligger mindre än 4 steg bort från talet 1.
Jag löste första uppgiften nu, min bild blev såhär:
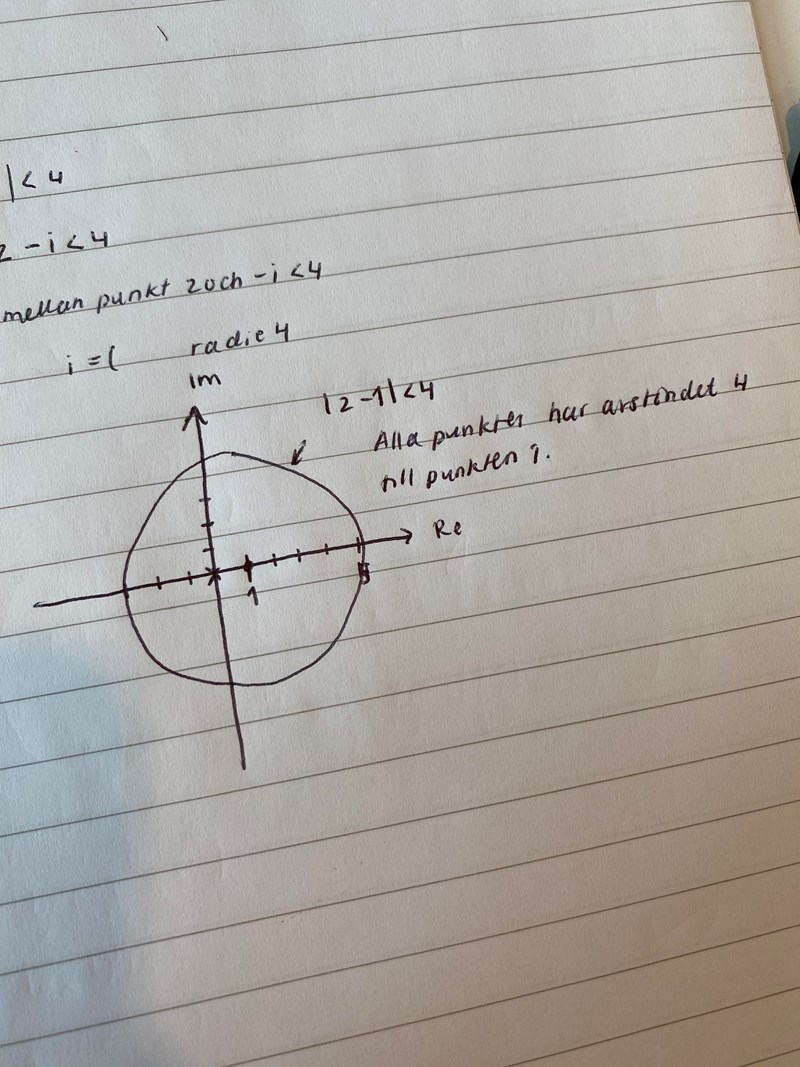
hur löser jag andra uppgiften?
Avståndet ska vara mindre än 4. Cirkeln markerar alla punkter som ligger exakt 4 steg bort. Så det är egentligen området inuti cirkeln du vill markera, inte själva cirkeln.
EDIT: För andra uppgiften: Vad säger likheten? Kan du tolka den i ord?
Skaft skrev:Avståndet ska vara mindre än 4. Cirkeln markerar alla punkter som ligger exakt 4 steg bort. Så det är egentligen området inuti cirkeln du vill markera, inte själva cirkeln.
EDIT: För andra uppgiften: Vad säger likheten? Kan du tolka den i ord?
juste, glömde markera, tack!
Ja den säger att alla punkter på cirkeln har avståndet z-10i till punkten 2i, och att den har sin medelpunkt i punkten 2i??
Nja inte riktigt:
Punkten z ska ha egenskapen: Avståndet mellan punkt och fixpunkten z=2i ska vara lika stort som avståndet mellan punkt och fixpunkten z=10i.
melinasde skrev:juste, glömde markera, tack!
Ja den säger att alla punkter på cirkeln har avståndet z-10i till punkten 2i, och att den har sin medelpunkt i punkten 2i??
Det blir ingen cirkel i b). Ett absolutbelopp beskriver bara ett avstånd, inget mer. Anledningen till att det blir en cirkel i a) är att avståndet från punkten (1,0) ska vara mindre än ett bestämt tal (4). Eftersom det inte är sagt nåt om riktning, kan man gå i vilken riktning som helst, men max 4 steg. De punkter man kan ta sig till utgör då en cirkelskiva kring (1,0).
I b) är situationen en annan. Som dr_lund skriver; nu vill vi istället markera alla punkter som har samma avstånd till 2i som till 10i.
Skaft skrev:melinasde skrev:juste, glömde markera, tack!
Ja den säger att alla punkter på cirkeln har avståndet z-10i till punkten 2i, och att den har sin medelpunkt i punkten 2i??
Det blir ingen cirkel i b). Ett absolutbelopp beskriver bara ett avstånd, inget mer. Anledningen till att det blir en cirkel i a) är att avståndet från punkten (1,0) ska vara mindre än ett bestämt tal (4). Eftersom det inte är sagt nåt om riktning, kan man gå i vilken riktning som helst, men max 4 steg. De punkter man kan ta sig till utgör då en cirkelskiva kring (1,0).
I b) är situationen en annan. Som dr_lund skriver; nu vill vi istället markera alla punkter som har samma avstånd till 2i som till 10i.
okej... tack så mycket båda ni men förstår fortfarande inte hur man ritar upp det....
Prova med ansatsen z=x+iy.
o s v. Vilken geometrisk figur får du?
melinasde skrev:okej... tack så mycket båda ni men förstår fortfarande inte hur man ritar upp det....
Börja med att markera talen 2i och 10i i talplanet. Hitta sen en punkt som ligger lika långt från båda. Hitta sen en till, och sen en till... det finns ett mönster som gör det lätt att markera alla.
Skaft skrev:melinasde skrev:okej... tack så mycket båda ni men förstår fortfarande inte hur man ritar upp det....
Börja med att markera talen 2i och 10i i talplanet. Hitta sen en punkt som ligger lika långt från båda. Hitta sen en till, och sen en till... det finns ett mönster som gör det lätt att markera alla.
Jag ritade upp det såhär och 6i låg först lika långt från båda?!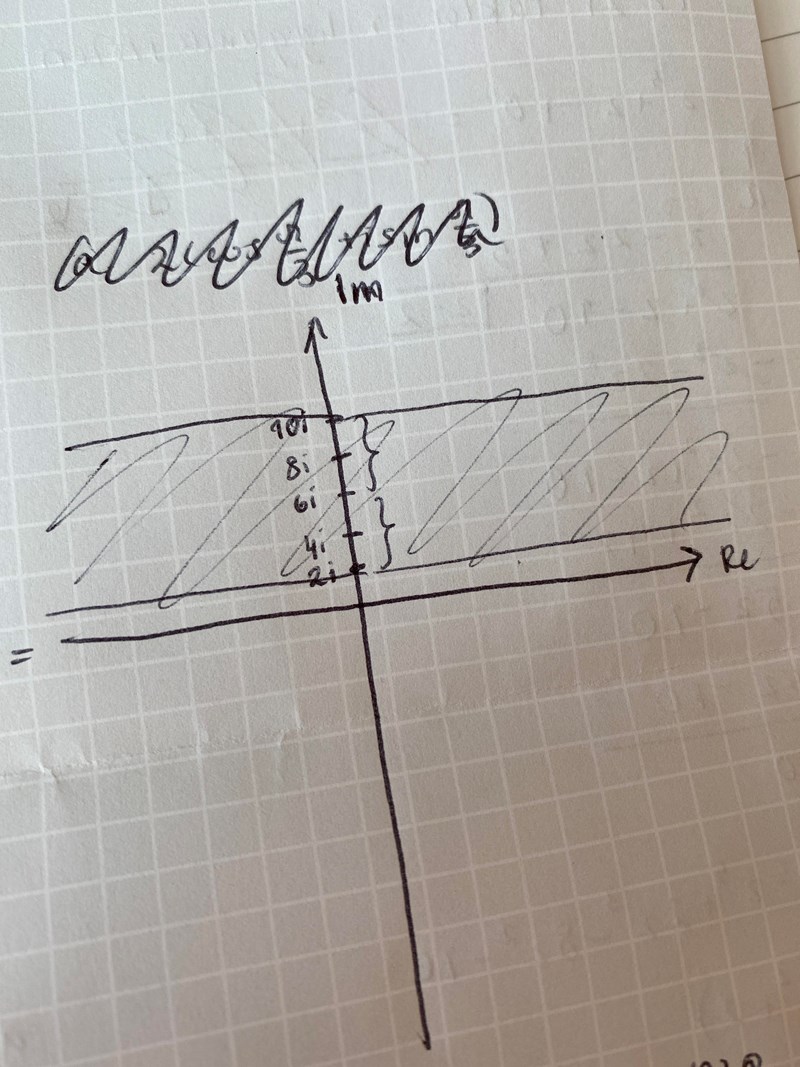
6i har helt riktigt lika långt till 10i som till 2i (4 steg). Men du har markerat en hel massa punkter där, t.ex. 8i. Från 8i är det 2 steg till 10i, och 6 steg till 2i. Inte samma!
Skaft skrev:6i har helt riktigt lika långt till 10i som till 2i (4 steg). Men du har markerat en hel massa punkter där, t.ex. 8i. Från 8i är det 2 steg till 10i, och 6 steg till 2i. Inte samma!
Hur ska man annars markera?
Bilden kommer sen, börja att plocka en punkt i taget. Är du med på varför 6i ska markeras, men inte 8i?
Jag vidhåller att du bör testa min algebraiska ansats.
Jag hjälper dig en bit. Efter användning av komplexa räkneregler:
.
Lös den ekvationen. Vad får du för resultat?
Skaft skrev:Bilden kommer sen, börja att plocka en punkt i taget. Är du med på varför 6i ska markeras, men inte 8i?
Ja för att det inte är lika avstånd, från 8i till 2i är det ju 6 steg och 10i till 8 är det 2, men jag förstår inte hur man ska visa detta, ska man bara markera 6i och inget mer? Eller hur menar du
dr_lund skrev:Jag vidhåller att du bör testa min algebraiska ansats.
Jag hjälper dig en bit. Efter användning av komplexa räkneregler:
.
Lös den ekvationen. Vad får du för resultat?
2y^2 + 16y - 96?
dr_lund skrev:Jag vidhåller att du bör testa min algebraiska ansats.
Jag hjälper dig en bit. Efter användning av komplexa räkneregler:
.
Lös den ekvationen. Vad får du för resultat?
Eller ja jag får x1 = 4 och X2= -12
melinasde skrev:Ja för att det inte är lika avstånd, från 8i till 2i är det ju 6 steg och 10i till 8 är det 2, men jag förstår inte hur man ska visa detta, ska man bara markera 6i och inget mer? Eller hur menar du
Uppgiften är bara att markera lösningarna. 6i är en lösning, så den ska ingå i markeringen. Du kan sätta en prick eller ett kryss eller nåt för att markera den. Men det är inte den enda punkten som har lika långt till både 2i och 10i. Undersök en annan punkt på samma höjd, t.ex. (1, 6i). Har den närmre till 10i eller 2i, eller lika långt?
Skaft skrev:melinasde skrev:Ja för att det inte är lika avstånd, från 8i till 2i är det ju 6 steg och 10i till 8 är det 2, men jag förstår inte hur man ska visa detta, ska man bara markera 6i och inget mer? Eller hur menar du
Uppgiften är bara att markera lösningarna. 6i är en lösning, så den ska ingå i markeringen. Du kan sätta en prick eller ett kryss eller nåt för att markera den. Men det är inte den enda punkten som har lika långt till både 2i och 10i. Undersök en annan punkt på samma höjd, t.ex. (1, 6i). Har den närmre till 10i eller 2i, eller lika långt?
Lika långt, och det blir också (2, 6i), (3,6i) osv... var det det du menade med mönster?
melinasde skrev:Lika långt, och det blir också (2, 6i), (3,6i) osv... var det det du menade med mönster?
Jajjebox. Hur blir figuren då, om du markerar alla dessa punkter (men inga andra, som 8i)?
Skaft skrev:melinasde skrev:Lika långt, och det blir också (2, 6i), (3,6i) osv... var det det du menade med mönster?
Jajjebox. Hur blir figuren då, om du markerar alla dessa punkter (men inga andra, som 8i)?
det blir väl bara såhär?
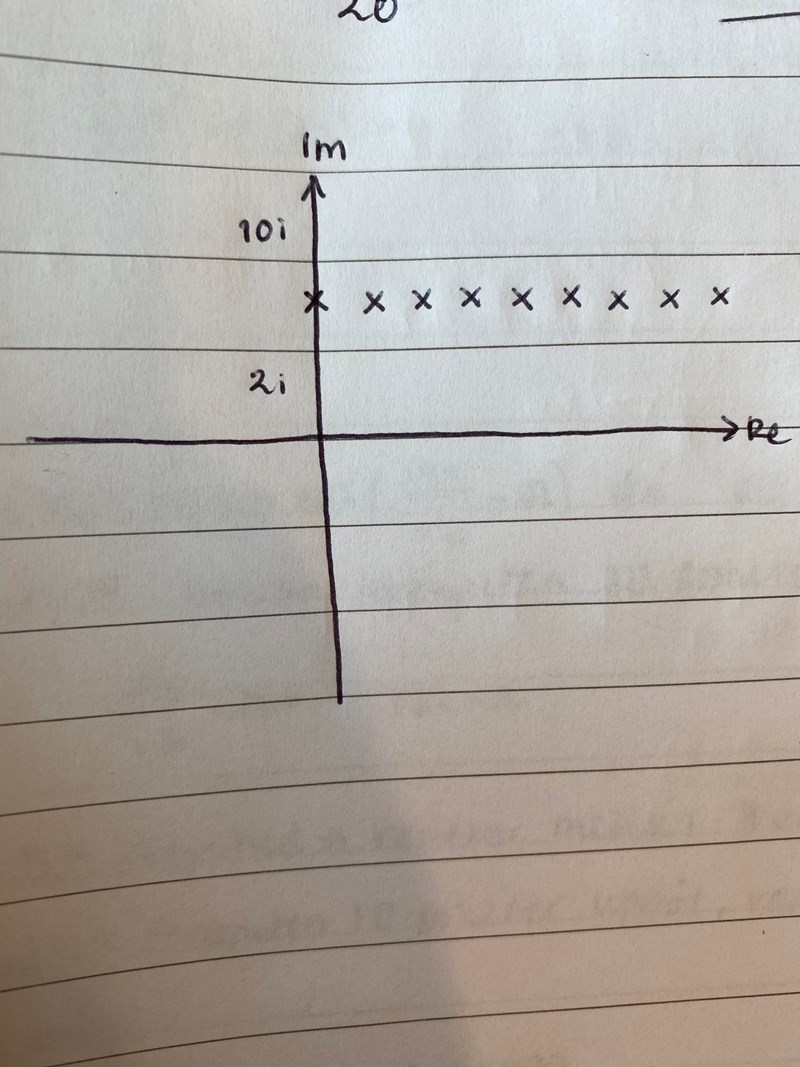
Du är nära nu! Men hur är det med punkterna som ligger mellan kryssen? Vi behöver inte begränsa oss till heltalskoordinater. Och är det annorlunda på andra sidan y-axeln (Im-axeln borde jag väl säga), eller kan man plocka punkter därifrån också?
Skaft skrev:Du är nära nu! Men hur är det med punkterna som ligger mellan kryssen? Vi behöver inte begränsa oss till heltalskoordinater. Och är det annorlunda på andra sidan y-axeln (Im-axeln borde jag väl säga), eller kan man plocka punkter därifrån också?
Hmmm ja det är sant blir samma på andra sidan också, ska man då istället göra en linje som går igenom allt så man också får alla koordinater mellan kryssen också?
Det tycker jag låter som en strålande idé =)
Nästan rätt. Du landar i ,
dvs räta linjen ( parallell med reella axeln) y=6.
Alla punkter på denna linje har samma avstånd till fixpunkterna. Fiffigt va?
Så förenades slutligen algebra och geometri.
dr_lund skrev:Nästan rätt. Du landar i ,
dvs räta linjen ( parallell med reella axeln) y=6.Alla punkter på denna linje har samma avstånd till fixpunkterna. Fiffigt va?
Så förenades slutligen algebra och geometri.
tack så hemskt mycket dr lund och skaft!!!! verkligen tack!




