Rita kurva till absolutbelopp

Hej allesammans!

Sitter och försöker rita grafen till: $\frac{|x - 1|}{2} - |x + 1|$

$|x - 1|$ = $\{\begin{cases} x - 1 o m x \geq 1 \\ - (x - 1) o m x < 1 \end{cases}$

$|x + 1|$ = $\{\begin{cases} x + 1 o m x \geq 1 \\ - (x + 1) o m x < 1 \end{cases}$

Det är här jag blir osäker. Ifall x $\leq$ (-1), kollar man då bägge absolutbeloppen samtidigt ifall det ska ske ett teckenbyte inom dessa? Likt:

$x \leq - 1 = - \frac{|x - 1|}{2} + |x + 1| \Rightarrow - \frac{x + 1}{2} + \frac{2 x + 2}{2} \Rightarrow \frac{x}{2} + \frac{3}{2}$

$x \geq 1$ = $\frac{|x - 1|}{2} - |x + 1| \Rightarrow \frac{x - 1}{2} - x - 1 \Rightarrow \frac{x - 1}{2} - \frac{2 x - 2}{2} \Leftrightarrow - \frac{x}{2} - \frac{3}{2}$

Här har jag nu funnit två grafer som stämmer för de olika olikheterna, det som jag fastnat på är hur man hittar

$- 1 \leq x \leq 1$ som ska skära de två tidigare graferna.

Tack på förhand

Jag ser mängder med teckenfel i mellanstegen, men det ser ut att bli rätt till slut.

Du ska inte byta tecken på uttrycket med absolutbelopp, du ska ersätta uttrycket innanför beloppsstrecken med antingen uttrycket självt eller med omvänt tecken.

Du menar att ifall x<(-1) så ändras endast:

-|x-1| / 2 till |x+1| / 2? Dvs att minustecknet inte är kvar framför?

Angående kurvan som skär de två redan beräknade ovan, får man den genom att ta ett värde mellan -1 < x < 1? Dvs att man tillämpar samma princip som ovan då tecknet inom absolutbeloppet ändras?

Tack på förhand

Dela in tallinjen i tre intervall istället:

x<-1

-1<x<1

x>1

Hur ser uttrycket ut i vart och ett av intervallen? Skriv ett förenklat uttryck för varje intervall. Rita gärna upp funktionen y=uttrycket i vardera intervallet, så ser man vad det är man försöker komma fram till.

Du gör ett par saker som är fel: du ändrar plötsligt $|x - 1|$ till - $|x - 1|$ , och du ändrar tecken inuti uttrycket: $|x - 1|$ blir $|x + 1|$ . Du måste klara ut varför du gör de här sakerna och förstå att det är fel.

Försök hitta alla teckenfel som jag pratade om i din första fråga.

Det enda du ska göra med ett absolutbelopputtryck, t.ex. $|x - 1|$ är att bestämma dig för (beroende på x) om det är lika med x-1 eller -(x-1).

Laguna, det var just teckenbyten jag skrev att jag blir förvirrad kring.

ifall x < -1: innebär det då att absolutbeloppet $\frac{|x - 1|}{2}$ byter tecken inuti eller utom. Ifall ( x < -1 ) så blir uttrycket $\frac{- (x - 1)}{2} \Rightarrow - \frac{x + 1}{2}$ , och det andra begreppet $|x + 1| s k r i v s o m t i l l - (x + 1)$ . Detta leder väl i sin tur till att

$- \frac{x + 1}{2} - (- \frac{2 (x + 1)}{2}) \Leftrightarrow - \frac{x + 1}{2} + \frac{2 x + 2}{2} \Rightarrow \frac{x}{2} + \frac{3}{2}$

Du gör det igen: du skriver $\frac{- (x - 1)}{2}$ och sedan att det blir $- \frac{x + 1}{2}$ . Det blir det inte, det blir $\frac{- x + 1}{2}$ .

Jag vet inte om problemen är rent skrivtekniska eller begreppsmässiga. Prova att sätta in lite olika x-värden.

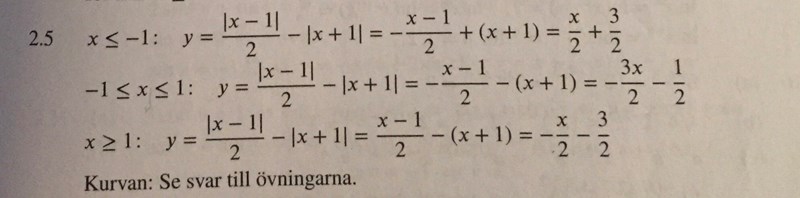
Bilden ovan är från Matematisk analys i en variabel av Göran Forsling. Stämmer inte denna ledningar till svar då?

Jo, men det är inte så du har gjort. Det tyder på att problemen är begreppsmässiga, när du inte verkar se skillnaden.

Ifall det är: -(x-1)/2 där det negativa tecknet ligger till vänster om bråkstrecket är jag med på noterna.

Vad är det som är -(x-1)/2?

Svara

Visa senaste svar