Rörelse uppgift: Två motorcyklar som accelererar. (C/A uppgift)

Hej, jag rekommenderar att rita två v/t-grafer i samma koordinatsystem. Det hjälper dig att sätta upp de nödvändig sambanden för att lösa uppgiften.

Yngve skrev:

Hej, jag rekommenderar att rita två v/t-grafer i samma koordinatsystem. Det hjälper dig att sätta upp de nödvändig sambanden för att lösa uppgiften.

Hej! Jag har ritat en v-t graf och genom att testa mig fram fick jag att t=5,5s. Undrar bara om det går att lösa denna uppgiften på ett algebraiskt sätt? Eller skulle det vara omöjligt? 

detta var mitt försök: 

$$\begin{gathered} \frac{5\times 5^2}{2} + 25t= \frac{3,57\times 7^2}{2}+ 25(t-2) \\ Jag kan få stäckan genom att använda forme\ln s=v0t+\frac{a{t}^2}{2} och s=vt. \\ Tyvärr blir det fel, eftersom det slutar med att tiden tar ut varandra. \\ Dessutom försökte jag stoppa in tiden 5,5s men det blev fel också. \end{gathered}$$

Stort tack Yngve ska börja göra fler vt-grafer när jag löser uppgifter. Tack igen!!!!

Människa skrev:

Yngve skrev:

Hej, jag rekommenderar att rita två v/t-grafer i samma koordinatsystem. Det hjälper dig att sätta upp de nödvändig sambanden för att lösa uppgiften.

Hej! Jag har ritat en v-t graf och genom att testa mig fram fick jag att t=5,5s. Undrar bara om det går att lösa denna uppgiften på ett algebraiskt sätt? Eller skulle det vara omöjligt? 

detta var mitt försök: 

$$\begin{gathered} \frac{5\times 5^2}{2} + 25t= \frac{3,57\times 7^2}{2}+ 25(t-2) \\ Jag kan få stäckan genom att använda forme\ln s=v0t+\frac{a{t}^2}{2} och s=vt. \\ Tyvärr blir det fel, eftersom det slutar med att tiden tar ut varandra. \\ Dessutom försökte jag stoppa in tiden 5,5s men det blev fel också. \end{gathered}$$

Stort tack Yngve ska börja göra fler vt-grafer när jag löser uppgifter. Tack igen!!!!

eller vänta i facit står det 5,3s fast jag får 5,5 s

Människa skrev:

Hej! Jag har ritat en v-t graf och genom att testa mig fram fick jag att t=5,5s. Undrar bara om det går att lösa denna uppgiften på ett algebraiskt sätt? Eller skulle det vara omöjligt? 

Jag brukar endast grovt skissa grafer som stöd för att sätta upp relevanta obekanta storheter, samband och ekvationer. Sedan brukar jag lösa uppgifterna algebraiskt.

Visa gärna dina v/t-grafer.

Yngve skrev:

Människa skrev:

Hej! Jag har ritat en v-t graf och genom att testa mig fram fick jag att t=5,5s. Undrar bara om det går att lösa denna uppgiften på ett algebraiskt sätt? Eller skulle det vara omöjligt? 

Jag brukar endast grovt skissa grafer som stöd för att sätta upp relevanta obekanta storheter, samband och ekvationer. Sedan brukar jag lösa uppgifterna algebraiskt.

Visa gärna dina v/t-grafer.

Jaha, kanske därför jag fick fel svar. Men här är min vt-graf som jag ritat. 

Människa skrev:

Yngve skrev:

Visa föregående citat

Människa skrev:

Visa föregående citat

Hej! Jag har ritat en v-t graf och genom att testa mig fram fick jag att t=5,5s. Undrar bara om det går att lösa denna uppgiften på ett algebraiskt sätt? Eller skulle det vara omöjligt? 

Jag brukar endast grovt skissa grafer som stöd för att sätta upp relevanta obekanta storheter, samband och ekvationer. Sedan brukar jag lösa uppgifterna algebraiskt.

Visa gärna dina v/t-grafer.

Jaha, kanske därför jag fick fel svar. Men här är min vt-graf som jag ritat. 

Jag tror jag har löst uppgiften. Jag fick rätt svar men om jag använde rätt metod vet jag inte. 

Människa skrev:

Jaha, kanske därför jag fick fel svar. Men här är min vt-graf som jag ritat. 

Bra skiss!

Motorcyklarnas accelerationer är

a_A = 25/5 m/s² = 5 m/s²

a_B = 25/7 m/s²

Vi kan konstatera att händelsen som efterfrågas inträffar någon gång i intervallet 5 s < t < 7 s, eftersom:

Motorcyklarnas respektive körda sträckor vid t = 5 s är

• s_A(5) = 5•5²/2 = 62,5 m
• s_B(5) = (25/7)•5²/2 $\approx$ 44,6 m

Dvs A har ännu inte hunnit 20 m längre än B.

Motorcyklarnas respektive körda sträckor vid t = 7 s är

• s_A(7) = 5•5²/2 + 25•(7-5) = 112,5 m
• s_B(7) = (25/7)•7²/2 ≈ 87,5 m

Dvs A har hunnit mer än 20 m längre än B.

=====

Tidpunkten då A hunnit 20 meter längre än B kan därför bestämma genom ekvationen

s_A(t) = s_B(t) + 20, där 5 < t < 7.

Dvs

5•5²/2+25•(t-5) = (25/7)•t²/2 + 20

Den enda lösningen som ligger i det aktuella intervallet är t $\approx$ 5,3 s.

Yngve skrev:

Människa skrev:

Jaha, kanske därför jag fick fel svar. Men här är min vt-graf som jag ritat. 

Bra skiss!

Motorcyklarnas accelerationer är

a_A = 25/5 m/s² = 5 m/s²

a_B = 25/7 m/s²

Vi kan konstatera att händelsen som efterfrågas inträffar någon gång i intervallet 5 s < t < 7 s, eftersom:

Motorcyklarnas respektive körda sträckor vid t = 5 s är

• s_A(5) = 5•5²/2 = 62,5 m
• s_B(5) = (25/7)•5²/2 $\approx$ 44,6 m

Dvs A har ännu inte hunnit 20 m längre än B.

Motorcyklarnas respektive körda sträckor vid t = 7 s är

• s_A(7) = 5•5²/2 + 25•(7-5) = 112,5 m
• s_B(7) = (25/7)•7²/2 ≈ 87,5 m

Dvs A har hunnit mer än 20 m längre än B.

=====

Tidpunkten då A hunnit 20 meter längre än B kan därför bestämma genom ekvationen

s_A(t) = s_B(t) + 20, där 5 < t < 7.

Dvs

5•5²/2+25•(t-5) = (25/7)•t²/2 + 20

Den enda lösningen som ligger i det aktuella intervallet är t $\approx$ 5,3 s.

Jaha, jag ser vart felet i min ekvation är. Stort tack Yngve!!!!

Bra. En intressant sak i sammanhanget är vad den andra lösningen dvs t $\approx$ 8,7 s. innebär rent fysiskt.

Kan du klura ut det?

(Du får då tänka dig att motorcykel B fortsätter att accelerera även efter 7 s.).

Yngve skrev:

Bra. En intressant sak i sammanhanget är vad den andra lösningen dvs t $\approx$ 8,7 s. innebär rent fysiskt.

Kan du klura ut det?

(Du får då tänka dig att motorcykel B fortsätter att accelerera även efter 7 s.).

Hej! Förlåt för att jag svarar så sent, jag åt lunch sen glömde jag helt bort att du hade skrivit. Men jag har tänkt länge nu och jag tror att det betyder att i början kommer A att leda, men sen kommer B att ha kört längre. Vid två tidpunkter dock (5,3s och 8,7s) kommer A att vara 20m före B. Är det rätt?? 

Jag skrev en ekvation, och blev lite förvirrad. Jag märkte att jag fick en andragrads ekvation, vilket vi inte jobbat med på matten så jag använde min graf ritande miniräknare. 

Ja, det stämmer.

• Ursprungligen (vid t = 0) är avståndet mellan motorcyklarna 0 meter.
• Eftersom A i inledningen har högre hastighet än B så ökar avståndet till 20 meter efter cirka 5,3 sekunder.
• Så länge A har en högre hastighet än B så ökar avståndet ännu mer.
• Men eftersom B, till skillnad mot A, fortsätter att accelerera så får B så småningom en högre hastighet än A och börjar då komma ikapp.
• Vid cirka 8,7 sekunder så har avståndet krympt till 20 meter igen.

Det är detta som den andra lösningen motsvarar.

Matematiken ger oss alltså svar vi inte ens har bett om 👍

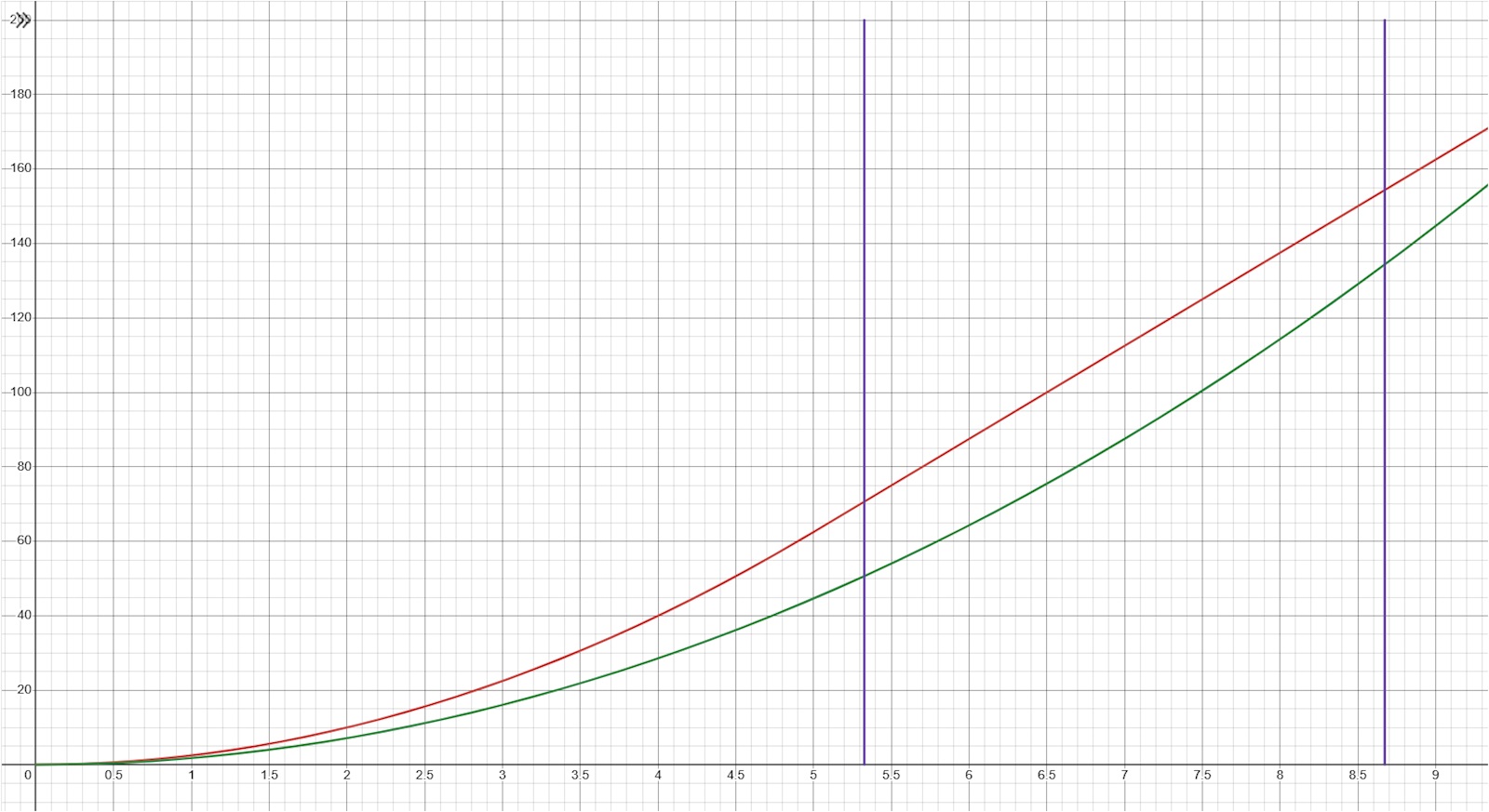
Här är en graf som visar hur långt motorcyklarna har kört vid olika tidpunkter:

• Den röda grafen visar motorcykel A: Först en parabel de första 5 sekunderna (acceleration), sedan en rät linje (konstant hastighet).
• Den gröna grafen visar motorcykel B: En parabel hela tiden (acceleration).
• De lila strecken visar var avståndet är just 20 meter.

Yngve skrev:

Ja, det stämmer.

• Ursprungligen (vid t = 0) är avståndet mellan motorcyklarna 0 meter.
• Eftersom A i inledningen har högre hastighet än B så ökar avståndet till 20 meter efter cirka 5,3 sekunder.
• Så länge A har en högre hastighet än B så ökar avståndet ännu mer.
• Men eftersom B, till skillnad mot A, fortsätter att accelerera så får B så småningom en högre hastighet än A och börjar då komma ikapp.
• Vid cirka 8,7 sekunder så har avståndet krympt till 20 meter igen.

Det är detta som den andra lösningen motsvarar.

Matematiken ger oss alltså svar vi inte ens har bett om 👍

---

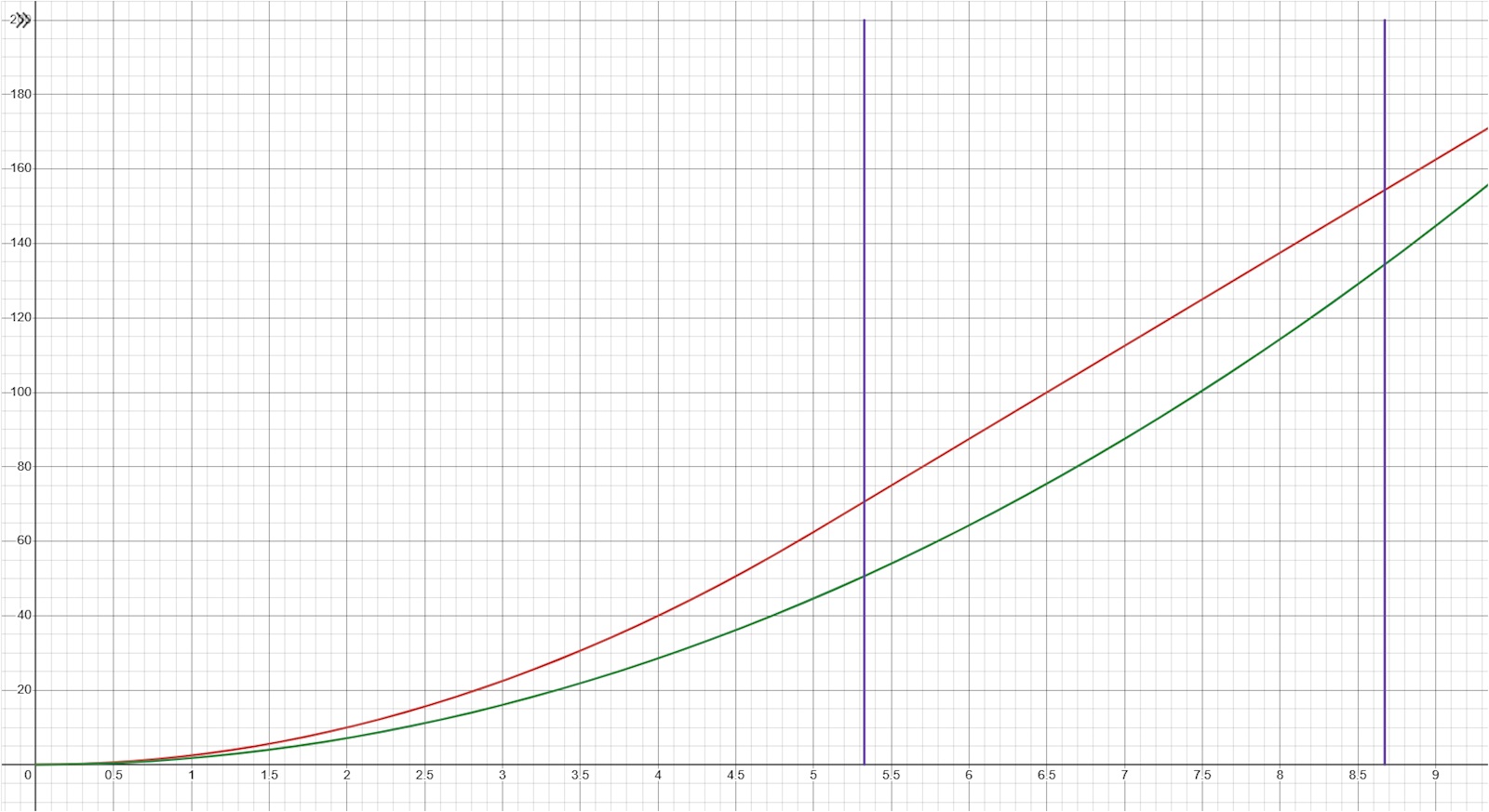
Här är en graf som visar hur långt motorcyklarna har kört vid olika tidpunkter:

• Den röda grafen visar motorcykel A: Först en parabel de första 5 sekunderna (acceleration), sedan en rät linje (konstant hastighet).
• Den gröna grafen visar motorcykel B: En parabel hela tiden (acceleration).
• De lila strecken visar var avståndet är just 20 meter.

Det är faktiskt väldigt intressant. Stort tack för att du visade mig det, jag uppskattar det verkligen! :)