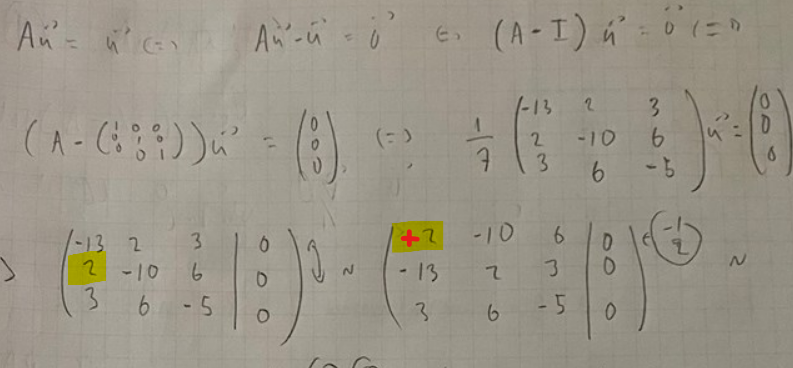Rotation
Har ingen aning om hur jag ska tänka... det enda jag fattar är att vi har en matris A s.a. om vi multiplicerar någon vektor i R^3 med matris A så kommer bilden ges av att vektorn roteras på något sätt....

En rotationsaxel förändras/transformeras ej vid rotationen, därför har vi
Au=u
om u är rotationsaxeln.
Trinity2 skrev:En rotationsaxel förändras/transformeras ej vid rotationen, därför har vi
Au=u
om u är rotationsaxeln.
kan du snälla förklara vad rotationsaxel är för något
brunbjörn skrev:Trinity2 skrev:En rotationsaxel förändras/transformeras ej vid rotationen, därför har vi
Au=u
om u är rotationsaxeln.
kan du snälla förklara vad rotationsaxel är för något
Tänk dig den lilla axel som sitter mitt i en klocka. På denna är det fäst vektorer i form av visare (tim, min och sekund). De kommer att ändra riktning när de roterar runt "mittaxeln" (rotationsaxeln), men den vektor som ligger i rotationsaxelns riktning ändras ej, då skulle axeln "vrida sig ur led" själv. Den enda vektor (som inte är 0) som inte påverkars av en rotation är den vektor som ligger i rotationsaxelns riktning.
Se även dessa
https://www.youtube.com/shorts/2VMvtzAb1dA
Skulle kroppen (som ligger i rotationsaxelns riktning) ändras med rotation skulle de snabbt bryta ryggraden. Kroppen består i samma riktning och form, den påverkas ej av rotationen.
Trinity2 skrev:brunbjörn skrev:Trinity2 skrev:En rotationsaxel förändras/transformeras ej vid rotationen, därför har vi
Au=u
om u är rotationsaxeln.
kan du snälla förklara vad rotationsaxel är för något
Tänk dig den lilla axel som sitter mitt i en klocka. På denna är det fäst vektorer i form av visare (tim, min och sekund). De kommer att ändra riktning när de roterar runt "mittaxeln" (rotationsaxeln), men den vektor som ligger i rotationsaxelns riktning ändras ej, då skulle axeln "vrida sig ur led" själv. Den enda vektor (som inte är 0) som inte påverkars av en rotation är den vektor som ligger i rotationsaxelns riktning.
Se även dessa
https://www.youtube.com/shorts/2VMvtzAb1dA
Skulle kroppen (som ligger i rotationsaxelns riktning) ändras med rotation skulle de snabbt bryta ryggraden. Kroppen består i samma riktning och form, den påverkas ej av rotationen.
så menar man den axeln allting snurrar runt? i R^2 en punkt, i R^3 en linje... lol borde fattat tack! men då håller jag med om att Au = u oavsett rotationen (för man skulle kunna tänka sig att vektorerna roterar 360 grader men det vi vet med 100% säkerhet är: trotts rotationen dvs trotts hur många grader vektorerna snurrar kring rotationsaxeln så gäller det att om vektorerna ligger i rotaationsaxeln så kommer de vektorerna vara i exakt samma position efter rotationen dvs. Au = u...
men hur fick facit det till att u = <1,2,3>t (de har ju inte med beräkningen) ?
brunbjörn skrev:Trinity2 skrev:brunbjörn skrev:Trinity2 skrev:En rotationsaxel förändras/transformeras ej vid rotationen, därför har vi
Au=u
om u är rotationsaxeln.
kan du snälla förklara vad rotationsaxel är för något
Tänk dig den lilla axel som sitter mitt i en klocka. På denna är det fäst vektorer i form av visare (tim, min och sekund). De kommer att ändra riktning när de roterar runt "mittaxeln" (rotationsaxeln), men den vektor som ligger i rotationsaxelns riktning ändras ej, då skulle axeln "vrida sig ur led" själv. Den enda vektor (som inte är 0) som inte påverkars av en rotation är den vektor som ligger i rotationsaxelns riktning.
Se även dessa
https://www.youtube.com/shorts/2VMvtzAb1dA
Skulle kroppen (som ligger i rotationsaxelns riktning) ändras med rotation skulle de snabbt bryta ryggraden. Kroppen består i samma riktning och form, den påverkas ej av rotationen.
så menar man den axeln allting snurrar runt? i R^2 en punkt, i R^3 en linje... lol borde fattat tack! men då håller jag med om att Au = u oavsett rotationen (för man skulle kunna tänka sig att vektorerna roterar 360 grader men det vi vet med 100% säkerhet är: trotts rotationen dvs trotts hur många grader vektorerna snurrar kring rotationsaxeln så gäller det att om vektorerna ligger i rotaationsaxeln så kommer de vektorerna vara i exakt samma position efter rotationen dvs. Au = u...
men hur fick facit det till att u = <1,2,3>t (de har ju inte med beräkningen) ?
Korrekt. Rotationsaxeln är "invariant" under rotationen/transformationen.
Om man man löser
Au=u
där u = (x,y,z) får man

och vi ser här att u kan skrivas
u=(1,2,3)t
(även om Mathematica ger ett annat format.)
Alltså har rotationsaxeln riktningsvektorn (1,2,3) (som inte är normerad, men det krävs ej i uppgiften).
Trinity2 skrev:brunbjörn skrev:Trinity2 skrev:brunbjörn skrev:Trinity2 skrev:En rotationsaxel förändras/transformeras ej vid rotationen, därför har vi
Au=u
om u är rotationsaxeln.
kan du snälla förklara vad rotationsaxel är för något
Tänk dig den lilla axel som sitter mitt i en klocka. På denna är det fäst vektorer i form av visare (tim, min och sekund). De kommer att ändra riktning när de roterar runt "mittaxeln" (rotationsaxeln), men den vektor som ligger i rotationsaxelns riktning ändras ej, då skulle axeln "vrida sig ur led" själv. Den enda vektor (som inte är 0) som inte påverkars av en rotation är den vektor som ligger i rotationsaxelns riktning.
Se även dessa
https://www.youtube.com/shorts/2VMvtzAb1dA
Skulle kroppen (som ligger i rotationsaxelns riktning) ändras med rotation skulle de snabbt bryta ryggraden. Kroppen består i samma riktning och form, den påverkas ej av rotationen.
så menar man den axeln allting snurrar runt? i R^2 en punkt, i R^3 en linje... lol borde fattat tack! men då håller jag med om att Au = u oavsett rotationen (för man skulle kunna tänka sig att vektorerna roterar 360 grader men det vi vet med 100% säkerhet är: trotts rotationen dvs trotts hur många grader vektorerna snurrar kring rotationsaxeln så gäller det att om vektorerna ligger i rotaationsaxeln så kommer de vektorerna vara i exakt samma position efter rotationen dvs. Au = u...
men hur fick facit det till att u = <1,2,3>t (de har ju inte med beräkningen) ?
Korrekt. Rotationsaxeln är "invariant" under rotationen/transformationen.
Om man man löser
Au=u
där u = (x,y,z) får man
och vi ser här att u kan skrivas
u=(1,2,3)t
(även om Mathematica ger ett annat format.)
Alltså har rotationsaxeln riktningsvektorn (1,2,3) (som inte är normerad, men det krävs ej i uppgiften).
Men jag får helt fel svar :( får vara triviala lösningen

Det finns ett teckenfel ganska tidigt i uträkningen:
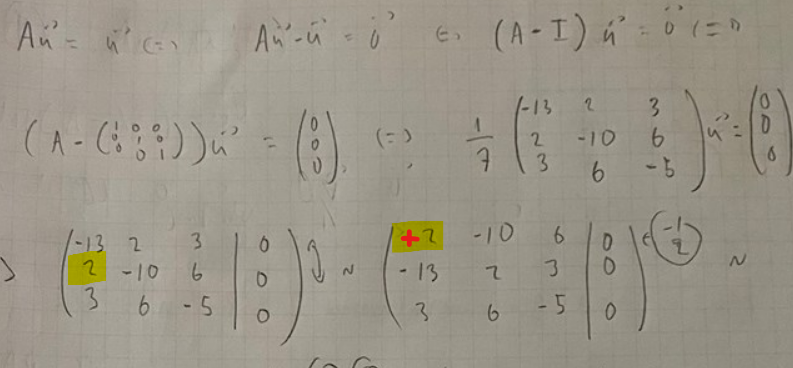
LuMa07 skrev:Det finns ett teckenfel ganska tidigt i uträkningen:
Tack fick rätt nu:
 Men är det fel att säga att rotationsaxeln ligger i den linjen? Facit säger ju att vektorn <1,2,3> är rotationsaxeln… låter konstigt att säga…
Men är det fel att säga att rotationsaxeln ligger i den linjen? Facit säger ju att vektorn <1,2,3> är rotationsaxeln… låter konstigt att säga…
angånde B uppgiften tänkte jag spontant att vi kan ta en vektor som inte ligger i rotationsaxeln, ex. v = <1,0,0>, sedan Av… sedan v • Av för att få hur mycket v har roterat… kan man tänka så? Dvs ta vilken vektor som helst istället för att ta fram ett plan som facit gjorde
Resultatet (1,2,3) är en riktningsvektor, det säger inget om var denna axel ligger i R^3.
B) Du kan ta vilken vektor som helst, men det är ibland svårt att tänka sig vad som händer med vektorn, eller beräkna rotationsvinkeln. Det gäller att välja "rätt" vektor.
Du tänker rätt, att t.ex. (1,0,0) är en "lätt" vektor men inte i detta fall. Det hade varit det om (0,0,1) hade varit rotationsaxelns riktning, men det är det inte.